Solved Examples and Worksheet for Writing Quadratic Equations for Line of Fit
A.
B.
C.
D.
Step: 1
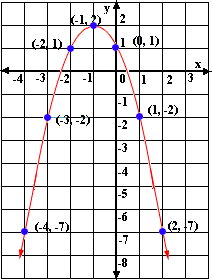
The equations y x x y x x
Step: 2
In the equation, y x x a b c
Step: 3
The x - b 2 a -(-2) 2(1)
[Replace b a
Step: 4
The y
[Replace x
Step: 5
Vertex (1, 0) is not a point on the graph, so the equation is not a solution for the graph.
Step: 6
In the equation, y x x a b c
Step: 7
The x - b 2 a -(-2) 2(-1)
[Replace b a
Step: 8
The y
[Replace x
Step: 9
From the graph the x y
Step: 10
So, the equation y x x
Correct Answer is : y x x
A.
B.
C.
D.
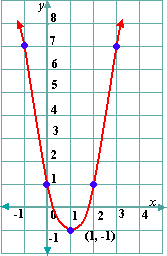
Step: 1
Step: 2
Step: 3
Step: 4
Step: 5
From the graph the x y
Step: 6
Correct Answer is : y x x
A.
B.
C.
D.
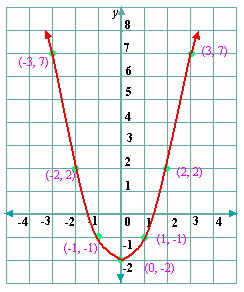
Step: 1
Step: 2
Step: 3
Step: 4
Step: 5
From the graph the x y
Step: 6
So, y x
Correct Answer is : y x
| Elapsed time | Volume |
| 0s | 25 cm3 |
| 5s | 23 cm3 |
| 10s | 20 cm3 |
| 15s | 15 cm3 |
| 20s | 13 cm3 |
| 25s | 9 cm3 |
A.
B.
C.
D.
Step: 1
The standard form of equation of a parabola is y ax b x c
Step: 2
Let′s pick the points (0, 25), (5, 23) and (10, 20) from the given table.
Step: 3
Substitute each point in equation (1)
Step: 4
25 = a b c
[Substititue the values.]
Step: 5
[Simplify.]
Step: 6
25a b c a b c
[Substitute the values.]
Step: 7
25
100
Step: 8
Solve (2) and (3) to get the values of a b
Step: 9
Step: 10
So, y x x
[Substitute the values.]
Correct Answer is : y x x
(Hint: Find a quadratic model for the data.)
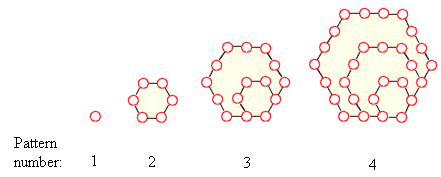
| Pattern number: | 1 | 2 | 3 | 4 |
| Number of dots: | 1 | 6 | 15 | 28 |
A. 210
B. 10
C. 190
D. 30
Step: 1
First find the quadratic model for the given pattern.
Step: 2
The standard form of equation of a parabola is y ax b x c
Step: 3
Equation (1) involves 3 unknowns a b c
Step: 4
The number of dots in the 3rd pattern is 15.
[Use the figure given.]
Step: 5
So, we have (1, 1), (2, 6) and (3, 15).
Step: 6
Substitute each point in equation (1)
Step: 7
4
9
Step: 8
Solving the equations (2), (3) and (4), we get the values of a b c a b c
Step: 9
So, y x x
[Replace a b c
Step: 10
Number of dots in the 10th pattern = 2(10)2 - (10)
[Replace x
Step: 11
= 2(100) - 10 = 190
Step: 12
So, there are 190 dots in the 10th pattern.
Correct Answer is : 190
| -2 | -1 | 0 | 1 | 2 | |
| 14 | -1 | 0 | 17 | 50 |
A.
B.
C.
D.
Step: 1
The equation of the given data could be a linear one or a quadratic one. Let′s consider the quadratic equation only. Because, when the coefficient of x a
Step: 2
Recall that the equation of a quadratic function is of the form:
y a x b x c
Step: 3
Pick out any 3 data pairs from the table. Let′s take: (0, 0), (1, 17) and (2, 50)
Step: 4
Substitute each pair in (1).
Step: 5
On substituting (0, 0), we get, c
Step: 6
On substituting (1, 17) and (2, 50), we get, a b c a b c
Step: 7
4
Step: 8
Solve (2) and (3) to get the values of a b a b
Step: 9
So, y x x
[Replace a b c
Correct Answer is : y x x
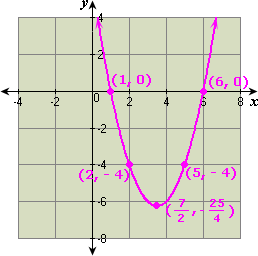
A.
B.
C.
D.
Step: 1
Step: 2
Step: 3
Step: 4
Step: 5
From the graph the x 7 2 y 25 4
Step: 6
So, y x x
Correct Answer is : y x x
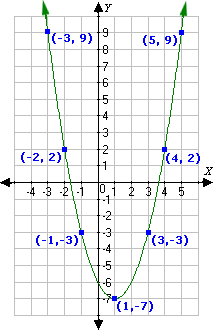
A.
B.
C.
D.
Step: 1
The equations y x x y x x
Step: 2
In the equation, y x x a b c
Step: 3
[Replace b a
Step: 4
[Replace x
Step: 5
Vertex (1, 2) is not a point on the graph, so the equation is not a solution for the graph.
Step: 6
In the equation, y x x a b c
Step: 7
[Replace b a
Step: 8
[Replace x
Step: 9
From the graph, x y
Step: 10
So, the equation y x x
Correct Answer is : y x x
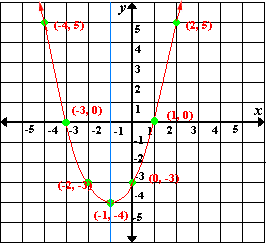
A.
B.
C.
D.
Step: 1
Step: 2
Step: 3
Step: 4
Step: 5
From the graph the x
they
the
Step: 6
So, the equation y x x
Correct Answer is : y x x
| Time (t) | Height (h) |
| 1 | 72 |
| 2 | 52 |
| 3 | 0 |
A.
B.
C.
D.
Step: 1
The standard form of equation of a parabola is y a x b x c
Step: 2
Let's pick the points (0, 60), (1, 72), and (3, 0) from the given table.
[Height of the building gives the point (0, 60).]
Step: 3
Substitute each point in equation (1)
Step: 4
60 = a b c
[Substitute the point (0, 60).]
Step: 5
Step: 6
[Substitute the points (1, 72) and (3, 0).]
Step: 7
9
Step: 8
Solve (2) and (3) to get the values of a b
Step: 9
Step: 10
So, h t t
[Replace a b c
Correct Answer is : h t t
- Constructing Line Plots-Algebra1-Solved Examples
- Constructing Histograms-Algebra1-Solved Examples
- Constructing Box-and-Whisker Plots-Algebra1-Solved Examples
- Reading and Interpreting Scatter plots-Algebra1-Solved Examples
- Constructing Scatter Plots and Line of Fit-Algebra1-Solved Examples
- Comparing Two Related Sets of Data and Expected Value-Algebra1-Solved Examples
- Identifying Outliers-Algebra1-Solved Examples
- Comparing Linear, Quadratic and Exponential Models-Algebra1-Solved Examples
- Correlation Coefficient, Causation and Correlation-Algebra1-Solved Examples
- Meaning of Slope and Intercepts in Graphs and Situations-Algebra1-Solved Examples
Related Worksheet
- Quadratic Equation