Solved Examples and Worksheet for Identifying Outliers
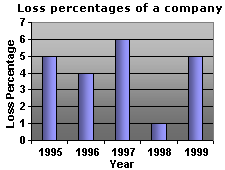
A. 6%, 1997
B. 2%, 1997
C. 1%, 1998
D. 5%, 1999
Step: 1
Outlier of a data set is the data value that is far apart from the remaining values.
Step: 2
The height of each bar in the graph indicate the percentage loss of the company during the particular year.
Step: 3
From the graph, the loss percentages in the last 5 years are 5%, 4%, 6%, 1% and 5%.
Step: 4
Among the values 1% is far apart from the remaining ones.
Step: 5
So, the outlier loss percentage is 1%, which occured in the year 1998.
Correct Answer is : 1%, 1998
A. $2
B. $3.50
C. $1
D. No outlier
Step: 1
Outlier is the data value which is far apart from the remaining values.
Step: 2
In the data, there is no value which is far apart from the rest of the values.
[All values are in the same range.]
Step: 3
So, there is no outlier for the data.
Correct Answer is : No outlier
A. 22
B. 21
C. No outlier
D. 26
Step: 1
An outlier is the data item which is far apart from the remaining values.
Step: 2
No data value among the values is far apart from the others.
Step: 3
So, there is no outlier for the data set.
Correct Answer is : No outlier
A. Median
B. Mean
Step: 1
Mean is a better measure of central tendency if there is no outlier for the data.
Step: 2
36 is the outlier of the data as it is far apart from other data values.
Step: 3
So, it may skew the central tendency.
Step: 4
As the outlier influences the mean, the median is the better measure of the central tendency.
Correct Answer is : Median
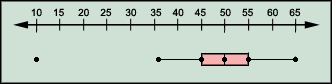
Step: 1
The outlier in a box-and-whisker plot is the data item, which is much higher or much lower than the other set of data items.
Step: 2
In the plot, the number 10 is much farther from the remaining set of data items.
Step: 3
So, the outlier in the plot is 10.
Correct Answer is : 10
A. Median
B. Range
C. Mode
D. Mean
Step: 1
Range is the difference between the maximum and minimum values of the data set.
Step: 2
Mode is used to find the occurrence of maximum times of a data value.
Step: 3
Mean is a better measure of central tendency if there is no outlier in the data.
Step: 4
27 is the outlier in the data as it is far apart from other values. So, it may skew the central tendency.
Step: 5
As the outlier influences the mean, the median is the better measure of the central tendency.
Correct Answer is : Median
A. Median
B. Mean
C. Mode
D. Range
Step: 1
Mean is a better measure of central tendency if there is no outlier for the data.
Step: 2
45 is the outlier of the data as it is far apart from other data values.
Step: 3
So, it may skew the central tendency.
Step: 4
As the outlier influences the mean, the median is the better measure of the central tendency.
Correct Answer is : Median
A. 76
B. 29
C. 60.5
D. no outlier
Step: 1
Arrange the weights of students in increasing order.
29, 36, 40, 45, 76
29, 36, 40, 45, 76
Step: 2
[Q
Step: 3
[Q Q
Step: 4
[Q Q
Step: 5
Interquartile Range (IQR Q Q
[Formula.]
Step: 6
= 60.5 - 32.5 = 28
Step: 7
To find the outlier, compute the cut-off points for outliers.
Step: 8
Lower fence = Q IQR
= 32.5 - 1.5(28) = - 9.5
= 32.5 - 1.5(28) = - 9.5
[Formula.]
Step: 9
Upper fence = Q IQR
= 60.5 + 1.5(28) = 102.5
= 60.5 + 1.5(28) = 102.5
[Formula]
Step: 10
If a data value is less than the lower fence or greater than the upper fence, then it is considered as an outlier.
Step: 11
There are no values that are less than - 9.5 or greater than 102.5.
Step: 12
So, there is no outlier.
Correct Answer is : no outlier
3.5, 4.7, 5.3, 6.8, 4.2, 5.8, 12.5
A. 2.6
B. 5.3
C. no outlier
D. 12.5
Step: 1
Arrange the data values in increasing order.
3.5, 4.2, 4.7, 5.3, 5.8, 6.8, 12.5
3.5, 4.2, 4.7, 5.3, 5.8, 6.8, 12.5
Step: 2
[Q
Step: 3
[Q Q
Step: 4
[Q Q
Step: 5
Interquartile Range (IQR Q Q
= 6.8 - 4.2 = 2.6
= 6.8 - 4.2 = 2.6
[Formula.]
Step: 6
To find the outlier, compute the cut-off points for outliers.
Step: 7
Lower fence = Q IQR
= 4.2 - 1.5(2.6) = 0.3
= 4.2 - 1.5(2.6) = 0.3
[Formula.]
Step: 8
Upper fence = Q IQR
= 6.8 + 1.5(2.6) = 10.7
= 6.8 + 1.5(2.6) = 10.7
Step: 9
If a data value is less than the lower fence or greater than the upper fence, then it is considered as an outlier.
Step: 10
The value 12.5 is greater than 10.7.
Step: 11
So, 12.5 is the outlier.
Correct Answer is : 12.5
A. 45
B. 7
C. 19
D. no outlier
Step: 1
Arrange the number of days taken in increasing order.
7, 8, 12, 15, 17, 19, 23, 45
7, 8, 12, 15, 17, 19, 23, 45
Step: 2
[Q
Step: 3
[Q Q
Step: 4
[Q Q
Step: 5
Interquartile Range(IQR Q Q
= 21 - 10 = 11
= 21 - 10 = 11
[Formula.]
Step: 6
To find the outlier, compute the cut-off points for outliers.
Step: 7
Lower fence = Q
= 10 - 1.5(11) = - 6.5
= 10 - 1.5(11) = - 6.5
[Formula]
Step: 8
Upper fence = Q IQR
= 21 + 1.5(11) = 37.5
= 21 + 1.5(11) = 37.5
[Formula]
Step: 9
If a data value is less than the lower fence or greater than the upper fence, then it is considered as an outlier.
Step: 10
The value 45 is greater than 37.5.
Step: 11
So, 45 is the outlier.
Correct Answer is : 45
- Writing Quadratic Equations for Line of Fit-Algebra1-Solved Examples
- Constructing Line Plots-Algebra1-Solved Examples
- Constructing Histograms-Algebra1-Solved Examples
- Constructing Box-and-Whisker Plots-Algebra1-Solved Examples
- Reading and Interpreting Scatter plots-Algebra1-Solved Examples
- Constructing Scatter Plots and Line of Fit-Algebra1-Solved Examples
- Comparing Two Related Sets of Data and Expected Value-Algebra1-Solved Examples
- Comparing Linear, Quadratic and Exponential Models-Algebra1-Solved Examples
- Correlation Coefficient, Causation and Correlation-Algebra1-Solved Examples
- Meaning of Slope and Intercepts in Graphs and Situations-Algebra1-Solved Examples