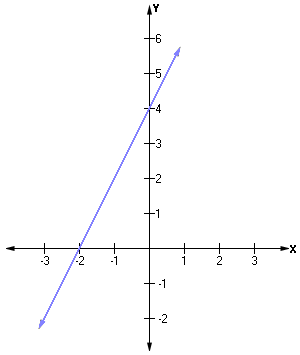Comparing Linear, Quadratic and Exponential Models-Algebra1-Solved Examples

Solved Examples and Worksheet for Comparing Linear, Quadratic and Exponential Models

Q1Which of the following models represents the equation y = ax² + bx + c?

A. Linear model
B. Quadratic model
C. Exponential model
D. Cubic model

Solutions

Step: 1

The equation y = ax² + bx + c represents a quadratic model.

Correct Answer is : Quadratic model

Q2Name the type of model that best fits the data collection: (- 1, - 1), (0, 1), (1, 3), (2, 5), (3, 7), (4, 9), (5, 11)

A. Linear model
B. Exponential model
C. Quadratic model
D. Cubic model

Solutions

Step: 1

Draw a scatter plot of the data.

Step: 2

Step: 3

From the graph, you can see that the points appear to lie on a line.

Step: 4

So, the type of model which best fits the data is a Linear model.

Correct Answer is : Linear model

Q3Name the type of model suggested by the graph.

A. Linear model
B. Quadratic model
C. Exponential model
D. Cubic model

Solutions

Step: 1

You can see that the graph is a straight line.

Step: 2

So, the type of model represents the graph is a Linear model.

Correct Answer is : Linear model

Q4Name the type of model suggested by the graph.

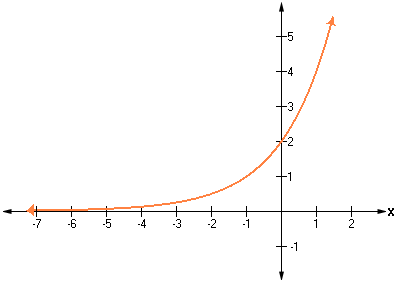
A. Quadratic model
B. Cubic model
C. Linear model
D. Exponential model

Solutions

Step: 1

You can see that the graph is an Exponential curve.

Step: 2

So, the type of model represents the graph is an Exponential model.

Correct Answer is : Exponential model

Q5Name the model that the graph of y = 1.3(0.82)^x represents.

A. Linear
B. Exponential growth
C. Exponential decay
D. Quadratic

Solutions

Step: 1

Make a table of values and draw a scatter plot.

Step: 2

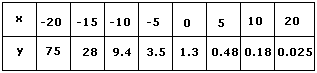
Step: 3

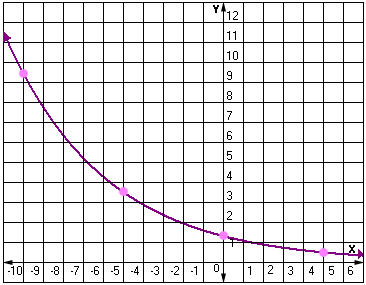
Step: 4

From the graph, you can see that the points appear to lie on an exponential curve.

Step: 5

As the x increases, then y decreases. So the graph of y = 1.3 (0.82)^x represents an exponential decay.

Correct Answer is : Exponential decay

Q6Tony has $500 in his bank account. The table shows the amount B available in the account after t years. Choose the model and its equation which best fits the situation.

Time(t)	0	1	2	3	4	5
Balance($) (B)	500	530	560	590	620	650

A. Linear; B = 500 + 30t
B. Exponential; B = 500 (1.06)^t
C. Quadratic; B = 500t²
D. Linear; B = 500 + 6t

Solutions

Step: 1

Draw a scatter plot of the data.

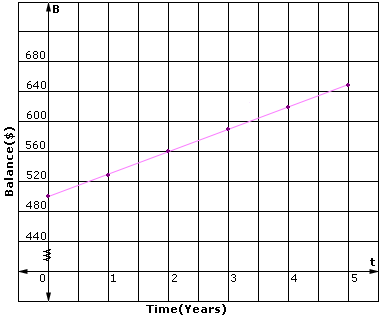
Step: 2

You can see that the graph is a straight line.

Step: 3

Find two points on the line such as (0, 500) and (1, 530).

Step: 4

m = y2 -y1x2 -x1 = 530 - 5001 - 0 = 30

[Find slope of the line.]

Step: 5

Using a y-intercept of 500 and a slope of m = 30, you can write an equation of the line.

Step: 6

B = mt + b

[Write slope-intercept form.]

Step: 7

B = 30t + 500

[Substitute 500 for b and 30 for m.]

Step: 8

So, the linear model B = 500 + 30t fits the data.

[Replace b with 500 and m with 30.]

Correct Answer is : Linear; B = 500 + 30t

Q7Name the type of model that best fits the data collection shown.

x	-1	0	1	2	3
y	-3	-1	1	3	5

A. Quadratic model
B. Exponential model
C. Cubic model
D. Linear model

Solutions

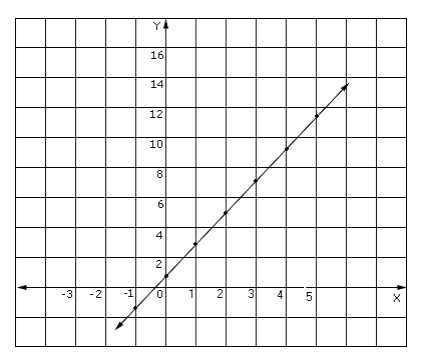
Step: 1

Draw a scatter plot of the data.

Step: 2

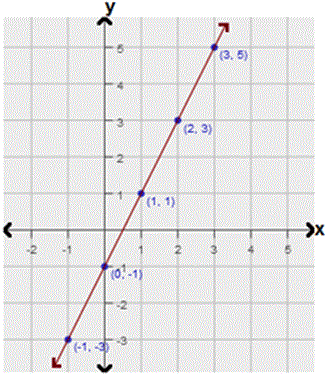
Step: 3

From the graph, it is observed that the points appear to lie on a line.

Step: 4

Therefore, the model that best fits the data is a linear model.

Correct Answer is : Linear model

Q8Which of the following equation represents an exponential model?
A. y = 2 - 3x
B. y = (2.1)x + 4
C. y = 4 + 2x²
D. y = 3(5.02)^x

Solutions

Step: 1

The equation y = 3(5.02)^x is of the form y = c(1 + r)^x.

Step: 2

So, the equation y = 3(5.02)^x represents an exponential model.

Correct Answer is : y = 3(5.02)^x

Q9Name the type of model that best fits the data collection shown.

x	-2	-1	0	1	2	3
y	-0.88	-0.5	0	1	3	7

A. Cubic model
B. Linear model
C. Exponential model
D. Quadratic model

Solutions

Step: 1

Draw a scatter plot of the data.

Step: 2

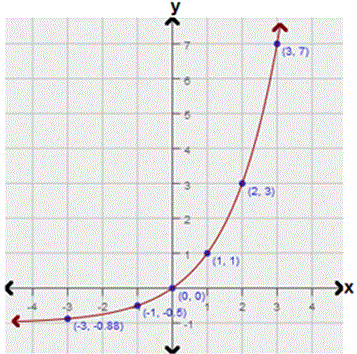
Step: 3

From the graph, it is observed that the points appear to lie on an exponential curve.

Step: 4

Therefore, the model that best fits the data is an exponential model.

Correct Answer is : Exponential model

Q10Which of the following equation represents an exponential model?
A. y = 8(1.14)^x
B. y = 3 + 4x²
C. y = 2x³ + 5
D. y = 4 - x

Solutions

Step: 1

The equation y = 8(1.14)^x is of the form y = c(1 + r)^x.

Step: 2

So, the equation y = 8(1.14)^x represents an exponential model.

Correct Answer is : y = 8(1.14)^x

Q11Which of the following equation represents a linear model?
A. y = 2(7.08)^x
B. y = 3x + 4
C. y = 4x³ - 3
D. y = 1 - 3x²

Solutions

Step: 1

The equation y = 3x + 4 is of the form y = mx + b.

Step: 2

So, the equation y = 3x + 4 represents a linear model.

Correct Answer is : y = 3x + 4

Q12Which of the following equation represents a quadratic model?
A. y = - 2x³ + 1
B. y = 4x² - 7
C. y = 8(3.26)^x
D. y = -2x - 3

Solutions

Step: 1

The equation y = 4x² - 7 is of the form y = ax² + bx + c.

Step: 2

So, the equation y = 4x² - 7 represents a quadratic model.

Correct Answer is : y = 4x² - 7

Solved Examples and Worksheet for Comparing Linear, Quadratic and Exponential Models

Related Worksheet

Related Topic

HighSchool Math