Solved Examples and Worksheet for Comparing Two Related Sets of Data and Expected Value
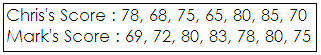
A. Chris has a higher median than Mark.
B. Chris has a higher mean than Mark.
C. Chris has a lower mean than Mark.
D. Chris has a same median than Mark.
Step: 1
Median is the data value which is the middle one in the ordered data set.
Step: 2
The middle value of Chris′s score is 65. Median of Chris′s score is 65.
Step: 3
The middle value of Mark′s score is 85. Median of Mark′s score is 83.
Step: 4
On comparing, Chris has a lower median than Mark.
[Since 65 is lower than 83.]
Step: 5
The average of the numbers of a data set is called mean.
Mean = s u m o f t h e d a t a v a l u e s n u m b e r o f d a t a v a l u e s
Step: 6
Mean of Chris′s score is 7 8 + 6 8 + 7 5 + 6 5 + 8 0 + 8 5 + 7 0 7
Step: 7
Mean of Mark′s score is 6 9 + 7 2 + 8 0 + 8 3 + 7 8 + 8 0 + 7 5 7
Step: 8
On comparing, Chris has a lower mean than Mark.
[Since 74.4 is lower than 76.7.]
Step: 9
So, Chris has a lower mean than Mark.
Correct Answer is : Chris has a lower mean than Mark.
A. Both data sets have equal median
B. Data B
C. Data A
Step: 1
Arrange the data values of Data A in ascending order: 120, 121, 122, 124, 128, 130, 133
Step: 2
Arrange the data values of Data B in ascending order: 112, 119, 120, 125, 126, 127, 128
Step: 3
Median is the middle data value in an ordered data set.
Step: 4
The middle value of Data A is 124. Median of Data A = 124
Step: 5
The middle value of Data B is 125. Median of Data B = 125
Step: 6
On comparing, Data B has a greater median than Data A.
[Since 125 is greater than 124.]
Correct Answer is : Data B
| Female Customers | 10 | 10 | 5 | 32 | 24 | 18 | 12 | 8 | 10 | 11 |
| Male Customers | 21 | 22 | 15 | 14 | 9 | 10 | 13 | 12 | 14 | 10 |
A. The mean of Female customers data is greater than that of Male customers data.
B. The mean of Female customers data is lesser than that of Male customers data.
C. The mean of Female customers data is equal to that of Male customers data.
Step: 1
The average of the numbers of a data set is called mean.
Mean =s u m o f t h e d a t a v a l u e s n u m b e r o f d a t a v a l u e s
Mean =
Step: 2
Mean of the number calls made daily by female customers = 1 0 + 1 0 + 5 + 3 2 + 2 4 + 1 8 + 1 2 + 8 + 1 0 + 1 1 1 0 = 1 4 0 1 0 = 1 4
[Substitute the values and simplify]
Step: 3
Mean of the number calls made daily by male customers = 2 1 + 2 2 + 1 5 + 1 4 + 9 + 1 0 + 1 3 + 1 2 + 1 4 + 1 0 1 0 = 1 4 0 1 0 = 1 4
[Substitute the values and simplify]
Step: 4
On comparing, the mean of the number of calls made daily by female customers is equal to the mean of the number of calls made daily by male customers.
Correct Answer is : The mean of Female customers data is equal to that of Male customers data.
| Data P | 6.3 | 6.1 | 6.7 | 6.6 | 6.8 | 6.4 |
| Data Q | 6.3 | 6.8 | 6.8 | 6.3 | 6.7 | 6.1 |
A. Both Data P and Data Q have equal median.
B. Data P has lesser median than Data Q
C. Data P has greater median than Data Q
Step: 1
Arrange the data values of Data P in ascending order: 6.1, 6.3, 6.4, 6.6, 6.7, 6.8
Step: 2
Arrange the data values of Data Q in ascending order: 6.1, 6.3, 6.3, 6.7, 6.8, 6.8
Step: 3
Median is the middle data value in an ordered data set.
Step: 4
Here we have two middle values. When there are two middle values, then Median = s u m o f t h e t w o m i d d l e v a l u e s 2
Step: 5
The two middle values of Data P are 6.4 and 6.6.
Median of Data P = 6 . 4 + 6 . 6 2 = 1 3 2 = 6 . 5
Step: 6
The two middle values of Data Q are 6.3 and 6.7.
Median of Data Q = 6 . 3 + 6 . 7 2 = 1 3 2 = 6 . 5
Step: 7
On comparing, both Data P and Data Q have equal median.
Correct Answer is : Both Data P and Data Q have equal median.
| Data P | 2.4 | 3.1 | 2.7 | 3.6 | 1.4 | 2.8 |
| Data Q | 3.8 | 2.5 | 1.8 | 1.3 | 2.4 | 2.1 |
A. Data P
B. Data Q
C. Both Data P and Data Q have equal interquartile range
Step: 1
The difference of Upper Quartile and Lower Quartile gives the value of interquartile range.
Step: 2
Arrange the data values of Data P in ascending order and find the lower quartile, upper quartile and interquartile range.
1.4, 2.4, 2.7, 2.8, 3.1, 3.6.
Lower Quartile = Median of lower half of the data = 2.4
Upper Quartile = Median of upper half of the data = 3.1
Interquartile Range = Upper Quartile - Lower Quartile = 3.1 - 2.4 = 0.7
1.4, 2.4, 2.7, 2.8, 3.1, 3.6.
Lower Quartile = Median of lower half of the data = 2.4
Upper Quartile = Median of upper half of the data = 3.1
Interquartile Range = Upper Quartile - Lower Quartile = 3.1 - 2.4 = 0.7
Step: 3
Arrange the data values of Data Q in ascending order and find the lower quartile, upper quartile and interquartile range.
1.3, 1.8, 2.1, 2.4, 2.5, 3.8.
Lower Quartile = Median of lower half of the data = 1.8
Upper Quartile = Median of upper half of the data = 2.5
Interquartile Range = Upper Quartile - Lower Quartile = 2.5 - 1.8 = 0.7
1.3, 1.8, 2.1, 2.4, 2.5, 3.8.
Lower Quartile = Median of lower half of the data = 1.8
Upper Quartile = Median of upper half of the data = 2.5
Interquartile Range = Upper Quartile - Lower Quartile = 2.5 - 1.8 = 0.7
Step: 4
Therefore, Data P and Data Q have equal interquartile range.
Correct Answer is : Both Data P and Data Q have equal interquartile range
| M | 12 | 18 | 13 | 21 | 17 | 16 | 24 | 15 |
| N | 17 | 11 | 24 | 27 | 15 | 23 | 20 | 13 |
A. Data M has lesser interquartile range than Data N.
B. Data M has greater interquartile range than Data N.
C. Both Data M and Data N has equal interquartile range.
Step: 1
The difference of Upper Quartile and Lower Quartile gives the value of interquartile range.
Step: 2
Arrange the data values of Data M in ascending order and find the lower quartile, upper quartile and interquartile range.
12, 13, 15, 16, 17, 18, 21, 24.
Lower Quartile = Median of lower half of the data =1 3 + 1 5 2 = 1 4
Upper Quartile = Median of upper half of the data =1 8 + 2 1 2 = 1 9 . 5
Interquartile Range = Upper Quartile - Lower Quartile = 19.5 - 14 = 5.5
12, 13, 15, 16, 17, 18, 21, 24.
Lower Quartile = Median of lower half of the data =
Upper Quartile = Median of upper half of the data =
Interquartile Range = Upper Quartile - Lower Quartile = 19.5 - 14 = 5.5
Step: 3
Arrange the data values of Data B in ascending order and find the lower quartile, upper quartile and interquartile range.
11, 13, 15, 17, 20, 23, 24, 27.
Lower Quartile = Median of lower half of the data =1 3 + 1 5 2 = 1 4
Upper Quartile = Median of upper half of the data =2 3 + 2 4 2 = 2 3 . 5
Interquartile Range = Upper Quartile - Lower Quartile = 23.5 - 14 = 9.5
11, 13, 15, 17, 20, 23, 24, 27.
Lower Quartile = Median of lower half of the data =
Upper Quartile = Median of upper half of the data =
Interquartile Range = Upper Quartile - Lower Quartile = 23.5 - 14 = 9.5
Step: 4
Therefore, Data M has lesser interquartile range than Data N.
[Since 5.5 is lesser than 9.5]
Correct Answer is : Data M has lesser interquartile range than Data N.
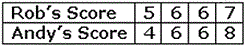
A. Rob
B. Andy
C. Both have an equal mean number of goals
Step: 1
Mean = s u m o f t h e d a t a v a l u e s n u m b e r o f d a t a v a l u e s
[Formula.]
Step: 2
Mean of the given data of Rob's score = 5 + 6 + 6 + 7 4 2 4 4
[Substitute and simplify.]
Step: 3
Mean of the given data of Andy's score = 4 + 6 + 6 + 8 4 2 4 4
[Substitute and simplify.]
Step: 4
On comparing, both have an equal mean number of goals.
Correct Answer is : Both have an equal mean number of goals
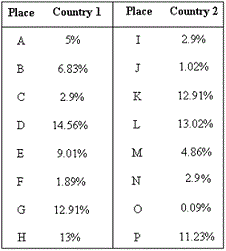
A. Country 1 has same median as Country 2
B. Country 1 has lesser median than Country 2
C. Country 1 has greater mean than Country 2
D. Country 1 has lesser mean than Country 2
Step: 1
Arrange the data values of Country 1 in ascending order: 1.89%, 2.9%, 5%, 6.83%, 9.01%, 12.91%, 13%, 14.56%.
Step: 2
Arrange the data values of Country 2 in ascending order: 0.09%, 1.02%, 2.9%, 2.9%, 4.86%, 11.23%, 12.91%, 13.02%.
Step: 3
Median is the middle data value in an ordered data set.
Step: 4
Here we have two middle values. When there are two middle values, then Median = s u m o f t h e t w o m i d d l e v a l u e 2
Step: 5
The two middle values of Country 1 are 6.83 and 9.01.
Median percentage of Country 1 = ( 6 . 8 3 + 9 . 0 1 ) 2
Step: 6
The two middle values of Country 2 are 2.9 and 4.86.
Median percentage of Country 2 = ( 2 . 9 + 4 . 8 6 ) 2
Step: 7
On comparing, Country 1 has a greater median than Country 2.
Step: 8
The average of the numbers of a data set is called mean.
Mean = s u m o f t h e d a t a v a l u e s n u m b e r o f d a t a v a l u e s
Step: 9
Mean percentage of children suffering from vascular diseases in Country 1
=( 5 + 6 . 8 3 + 2 . 9 + 1 4 . 5 6 + 9 . 0 1 + 1 . 8 9 + 1 2 . 9 1 + 1 3 ) 8
=
Step: 10
Step: 11
= 8.263%
Step: 12
Mean percentage of children suffering from vascular diseases in Country 2
=( 2 . 9 + 1 . 0 2 + 1 2 . 9 1 + 1 3 . 0 2 + 4 . 8 6 + 2 . 9 + 0 . 0 9 + 1 1 . 2 3 ) 8
=
Step: 13
= 4 8 . 9 3 8
Step: 14
= 6.116%
Step: 15
On comparing, Country 1 has greater mean percentage than Country 2.
[Since 8.263 is greater than 6.116.]
Step: 16
So, Country 1 has greater mean percentage than country 2.
Correct Answer is : Country 1 has greater mean than Country 2
| Company A | 4 | 5 | 5 | 5 | 5 | 6 | 7 | 6 | 4 | 5 |
| Company B | 5 | 5 | 8 | 8 | 8 | 10 | 6 | 5 | 8 | 7 |
A. Company A
B. Company B
Step: 1
The average of the numbers of a data set is called mean.
Mean =s u m o f t h e d a t a v a l u e s n u m b e r o f d a t a v a l u e s
Mean =
Step: 2
Mean hourly pay for Company A = ( 4 + 5 + 5 + 5 + 5 + 6 + 7 + 6 + 4 + 5 ) 1 0 = 5 2 1 0 = $ 5 . 2
[Substitute the values and simplify]
Step: 3
Mean hourly pay for Company B = ( 5 + 5 + 8 + 8 + 8 + 1 0 + 6 + 5 + 8 + 7 ) 1 0 = 7 0 1 0 = $ 7
[Substitute the values and simplify]
Step: 4
On comparing, Company B has higher mean hourly pay than Company A. So, Phillips would join the Company B.
Correct Answer is : Company B
| Edward | 90 | 70 | 50 | 45 | 65 |
| Richard | 85 | 40 | 60 | 75 | 80 |
A. Both have equal standard deviation
B. Richard
C. Edward
Step: 1
To find the standard deviation first we need to find the mean of the data.
Mean =s u m o f t h e d a t a v a l u e s n u m b e r o f d a t a v a l u e s
Mean =
Step: 2
Mean (X) of stamps of different countries collected by Edward = ( 9 0 + 7 0 + 5 0 + 4 5 + 6 5 ) 5 = 3 2 0 5 = 6 4
Step: 3
Mean (Y) of stamps of different countries collected by Richard = ( 8 5 + 4 0 + 6 0 + 7 5 + 8 0 ) 5 = 3 4 0 5 = 6 8
Step: 4
Standard deviation = ( x 1 - X ) 2 + ( x 2 - X ) 2 + . . . + ( x n - X ) 2 n
[X = mean of the data, x x x
Step: 5
Standard deviation of stamps collected by Edward = ( x 1 - X ) 2 + ( x 2 - X ) 2 + ( x 3 - X ) 2 + ( x 4 - X ) 2 + ( x 5 - X ) 2 n
=( 9 0 - 6 4 ) 2 + ( 7 0 - 6 4 ) 2 + ( 5 0 - 6 4 ) 2 + ( 4 5 - 6 4 ) 2 + ( 6 5 - 6 4 ) 2 5
=6 7 6 + 3 6 + 1 9 6 + 3 6 1 + 1 5
=1 2 7 0 5
=2 5 4
= 15.94
=
=
=
=
= 15.94
Step: 6
Standard deviation of stamps collected by Richard = ( y 1 - Y ) 2 + ( y 2 - Y ) 2 + ( y 3 - Y ) 2 + ( y 4 - Y ) 2 + ( y 5 - Y ) 2 n
=( 8 5 - 6 8 ) 2 + ( 4 0 - 6 8 ) 2 + ( 6 0 - 6 8 ) 2 + ( 7 5 - 6 8 ) 2 + ( 8 0 - 6 8 ) 2 5
=2 8 9 + 7 8 4 + 6 4 + 4 9 + 1 4 4 5
=1 3 3 0 5
=2 6 6
= 16.31
=
=
=
=
= 16.31
Step: 7
On comparing, Richard has greater standard deviation than Edward.
Correct Answer is : Richard
- Writing Quadratic Equations for Line of Fit-Algebra1-Solved Examples
- Constructing Line Plots-Algebra1-Solved Examples
- Constructing Histograms-Algebra1-Solved Examples
- Constructing Box-and-Whisker Plots-Algebra1-Solved Examples
- Reading and Interpreting Scatter plots-Algebra1-Solved Examples
- Constructing Scatter Plots and Line of Fit-Algebra1-Solved Examples
- Identifying Outliers-Algebra1-Solved Examples
- Comparing Linear, Quadratic and Exponential Models-Algebra1-Solved Examples
- Correlation Coefficient, Causation and Correlation-Algebra1-Solved Examples
- Meaning of Slope and Intercepts in Graphs and Situations-Algebra1-Solved Examples
Related Worksheet
- Customary System Of Measurement