Solved Examples and Worksheet for Correlation Coefficient, Causation and Correlation
A. there is no causal factor present between the two
B. causal factor is present between the two
C. if correlation exists then causation exists
D. correlation doesn′t imply causation
Step: 1
Correlation is a measure of the strength of the relationship between two variables. It is used to predict the value of one variable given the value of the other.
Step: 2
Causation is the act of causing one variable to happen due to the other variable's effect.
Step: 3
Eating junk food makes you obese therefore there is a causal factor present.
Correct Answer is : causal factor is present between the two
A. I dont know
B. correlation doesn′t imply causation
C. if correlation exists then causation exists
D. only correlation exists
Step: 1
Correlation is a measure of the strength of the relationship between two variables. It is used to predict the value of one variable given the value of the other.
Step: 2
Causation is the act of causing one variable to happen due to the other variable's effect
Step: 3
Eating junk food makes you obese therefore there is a causal factor present.
Correct Answer is : correlation doesn′t imply causation
A. There is both correlation and causation.
B. There is causation but no correlation.
C. There is a correlation but no causation.
D. There is neither correlation nor causation.
Step: 1
Correlation is a measure of the strength of the relationship between two variables. It is used to predict the value of one variable given the value of the other.
Step: 2
Causation is the act of causing one variable to happen due to the other variable's effect.
Step: 3
There is direct relation of correlation and causation as student's scores increases his cumulative GPA also increases.
Correct Answer is : There is both correlation and causation.
A. There is causation but no correlation.
B. There is neither correlation nor causation.
C. There is both correlation and causation.
D. There is a correlation but no causation.
Step: 1
Correlation is a measure of the strength of the relationship between two variables. It is used to predict the value of one variable given the value of the other.
Step: 2
Causation is the act of causing one variable to happen due to the other variable's effect.
Step: 3
In the problem, the age of truck and the cost of repairs are the two variables.
Step: 4
If the age of truck is more, then the cost of repairs is also more. So, there exists a causal factor between the two.
Step: 5
Therefore, both correlation and causation exists.
Correct Answer is : There is both correlation and causation.
A. There is both correlation and causation.
B. There is a correlation but no causation.
C. There is neither correlation nor causation.
D. There is causation but no correlation.
Step: 1
Correlation is a measure of the strength of the relationship between two variables. It is used to predict the value of one variable given the value of the other.
Step: 2
Causation is the act of causing one variable to happen due to the other variable's effect.
Step: 3
In the problem, the money spent on R & D and the firm's annual profits are the two variables.
Step: 4
If the money spent on R & D is more, then the firm's annual profit is also more. So, there exists a causal factor between the two.
Step: 5
Therefore, both correlation and causation exists.
Correct Answer is : There is both correlation and causation.
| Student | Hours of study( | Test scores ( |
| A | 6 | 48 |
| B | 12 | 72 |
| C | 8 | 65 |
| D | 10 | 70 |
| E | 12 | 78 |
| F | 7 | 65 |
| G | 12 | 82 |
| H | 6 | 50 |
| I | 14 | 85 |
| J | 15 | 90 |
A. - 0.953; strong negative relationship
B. 0.953; strong positive relationship
C. - 0.173; weak negative relationship
D. 0.173; weak positive relationship
Step: 1
Prepare a table for values x y x y xy
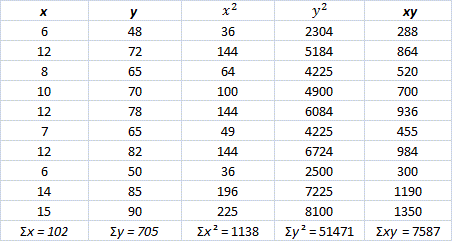

Step: 2
Correlation coefficient,r n ( Σ x y ) - ( Σ x ) ( Σ y ) [ n ( Σ x 2 ) - ( Σ x ) 2 ] [ n ( Σ y 2 ) - ( Σ y ) 2 ]
[Formula]
Step: 3
[Substitute the values from the table and simplify.]
Step: 4
Step: 5
Therefore, there is a strong positive relationship between the hours of study and test scores .
[When r
Correct Answer is : 0.953; strong positive relationship
| -2 | -1 | 0 | 1 | 2 | |
| 64 | 1 | 0 | 1 | 64 |
A. false; there does not exist a relationship
B. false; two uncorrelated variables are always independent
C. true; there exists a relation between
D. true; two uncorrelated variables are always dependent
Step: 1
Make a table with values for x y x y xy
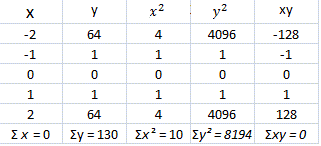
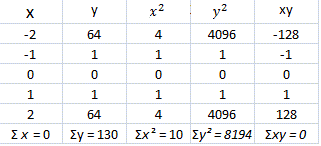
Step: 2
Correlation coefficient, r n ( Σ x y ) - ( Σ x ) ( Σ y ) [ n ( Σ x 2 ) - ( Σ x ) 2 ] [ n ( Σ y 2 ) - ( Σ y ) 2 ]
[Substitute the values from the table and simplify.]
Step: 3
Therefore, x y
Step: 4
But, we can see that x y y x
Step: 5
Therefore, two uncorrelated variables need not be independent, i.e., they can be dependent also.
Correct Answer is : true; there exists a relation between x y y x
| Height(in inches) | 60 | 62 | 64 | 66 | 66 |
| Shoe size(in inches) | 7 | 8 | 9 | 10 | 11 |
A. - 0.98; strong negative relationship
B. 1; strong positive relationship
C. -1; strong positive relationship
D. 0.98; strong negative relationship
Step: 1
Make a table with values for x y x y xy
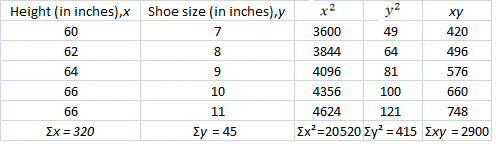
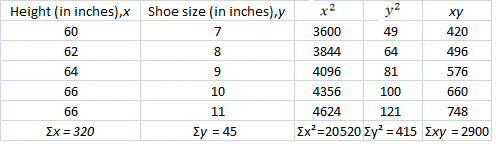
Step: 2
Correlation coefficient, r n ( Σ x y ) - ( Σ x ) ( Σ y ) [ n ( Σ x 2 ) - ( Σ x ) 2 ] [ n ( Σ y 2 ) - ( Σ y ) 2 ]
[Substitute the values from the table.]
Step: 3
[Simplify.]
Step: 4
Step: 5
Therefore, there is a strong positive relationship between the heights and their shoe sizes of 5 people .
[When r r
Correct Answer is : 1; strong positive relationship
| Average temperature(in °F) | 42.3 | 40.2 | 41.8 | 42.9 | 43.1 | 42.6 | 40.7 |
| Average precipitation(in cm) | 0.85 | 1.72 | 0.69 | 2.77 | 2.46 | 1.89 | 0.64 |
A. 0.76
B. - 0.54
C. 0.54
D. - 0.76
Step: 1
Make a table with values for x y x y xy
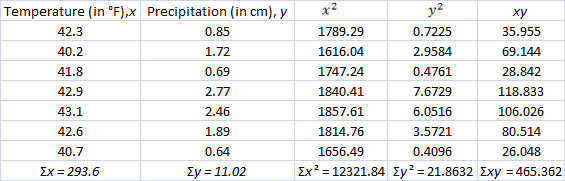

Step: 2
Correlation coefficient, r n ( Σ x y ) - ( Σ x ) ( Σ y ) [ n ( Σ x 2 ) - ( Σ x ) 2 ] [ n ( Σ y 2 ) - ( Σ y ) 2 ]
[Substitute the values from the table.]
Step: 3
[Simplify.]
Step: 4
The correlation coefficient, r
Correct Answer is : 0.54
| 34 | 31 | 35 | 30 | 32 | 35 | 32 | 33 | |
| 35 | 32 | 30 | 31 | 34 | 30 | 33 | 35 |
A. - 0.134; weak negative relationship
B. 0.1506; weak positive relationship
C. - 0.1506; weak negative relationship
D. 0.134; weak positive relationship
Step: 1
Make a table with values for x y x y xy
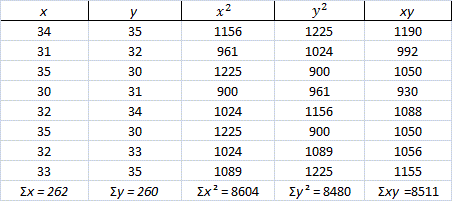

Step: 2
Correlation coefficient, r n ( Σ x y ) - ( Σ x ) ( Σ y ) [ n ( Σ x 2 ) - ( Σ x ) 2 ] [ n ( Σ y 2 ) - ( Σ y ) 2 ]
[Substitute the values from the table.]
Step: 3
[Simplify.]
Step: 4
Step: 5
Therefore, there is weak negative relationship between the variables.
[When r r
Correct Answer is : - 0.1506; weak negative relationship
| Student | A | B | C | D | E | F | G | H | I | J |
| Midterm scores( | 76 | 68 | 66 | 83 | 90 | 72 | 79 | 92 | 96 | 87 |
| Final scores( | 71 | 75 | 79 | 77 | 84 | 68 | 82 | 98 | 88 | 93 |
A. 2.105
B. 0.752
C. 1.243
D. 0.141
Step: 1
Prepare a table for values x y x y xy
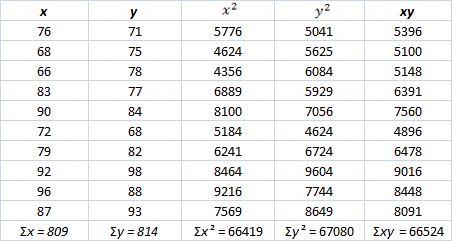

Step: 2
Correlation coefficient, r n ( Σ x y ) - ( Σ x ) ( Σ y ) [ n ( Σ x 2 ) - ( Σ x ) 2 ] [ n ( Σ y 2 ) - ( Σ y ) 2 ]
[Substitute the values from the table.]
Step: 3
[Simplify.]
Step: 4
The correlation coefficient, r
Correct Answer is : 0.752
| Temperature °C( | Ice Cream Sales ( |
| 14.2° | $210 |
| 16.4° | $320 |
| 11.9° | $185 |
| 15.2° | $328 |
| 18/5° | $410 |
| 22.1° | $518 |
| 19.4° | $416 |
A. -0.975
B. -0.645
C. 0.975
D. 0.645
Step: 1
Prepare a table for values x y x y xy
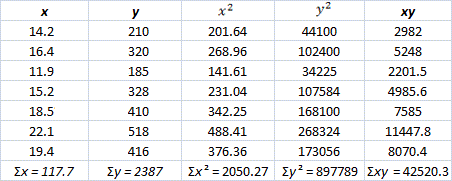
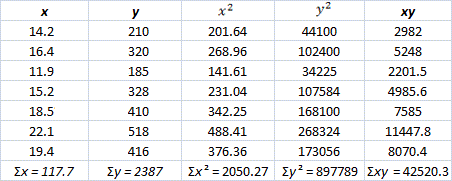
Step: 2
Correlation coefficient, r n ( Σ x y ) - ( Σ x ) ( Σ y ) [ n ( Σ x 2 ) - ( Σ x ) 2 ] [ n ( Σ y 2 ) - ( Σ y ) 2 ]
[Substitute the values from the table.]
Step: 3
[Simplify.]
Step: 4
Step: 5
Therefore, there is a strong positive relationship between the temperature and ice cream sales.
[When r r
Correct Answer is : 0.975
| Speed( | Time( |
| 50 | 50 |
| 55 | 40 |
| 60 | 42 |
| 65 | 35 |
| 70 | 36 |
A. 1.321
B. -1.321
C. -1.098
D. 1.098
Step: 1
Prepare a table for values x y x y xy
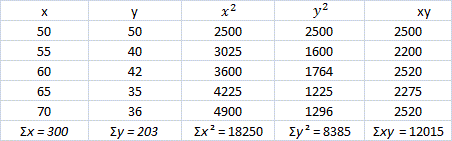
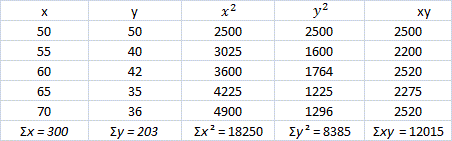
Step: 2
Correlation coefficient, r n ( Σ x y ) - ( Σ x ) ( Σ y ) [ n ( Σ x 2 ) - ( Σ x ) 2 ] [ n ( Σ y 2 ) - ( Σ y ) 2 ]
[Formula.]
Step: 3
[Substitute the values from the table and simplify.]
Step: 4
Step: 5
The correlation coefficient, r
Correct Answer is : 1.321
- Writing Quadratic Equations for Line of Fit-Algebra1-Solved Examples
- Constructing Line Plots-Algebra1-Solved Examples
- Constructing Histograms-Algebra1-Solved Examples
- Constructing Box-and-Whisker Plots-Algebra1-Solved Examples
- Reading and Interpreting Scatter plots-Algebra1-Solved Examples
- Constructing Scatter Plots and Line of Fit-Algebra1-Solved Examples
- Comparing Two Related Sets of Data and Expected Value-Algebra1-Solved Examples
- Identifying Outliers-Algebra1-Solved Examples
- Comparing Linear, Quadratic and Exponential Models-Algebra1-Solved Examples
- Meaning of Slope and Intercepts in Graphs and Situations-Algebra1-Solved Examples
Related Worksheet
- Variable