Solving and Graphing Absolute Value Inequalities-Algebra1-Solved Examples

Solved Examples and Worksheet for Solving and Graphing Absolute Value Inequalities

Q1A rope is cut into 7 equal pieces. A small piece of 2 ft is again cut from each of the 7 pieces. Choose the correct variable expression for the new length of each piece.

A. (x7 - 2) ft
B. (x2 - 7) ft
C. (2 - x7) ft
D. (x7 + 2) ft

Solutions

Step: 1

Let x be the length of the original rope.

Step: 2

Length of each of the 7 pieces = x7 ft

Step: 3

The variable expression for the new length of each piece is (x7- 2) ft.

[A length of 2 ft is cut from each of the 7 pieces.]

Correct Answer is : (x7 - 2) ft

Q2Identify a variable expression for the word phrase '13 more than 8 times a number'.
A. 13n + 8
B. 8n + 13
C. n + 91
D. 8n - 13

Solutions

Step: 1

Let n be a number.

Step: 2

13 more than 8 times a number = 8n + 13.

[Write the expression.]

Step: 3

So, the variable expression for the phrase is 8n + 13.

Correct Answer is : 8n + 13

Q3Write a variable expression for the phrase, 'the number of days in n weeks'.
A. n - 7
B. 7n
C. 7 + n
D. 7n

Solutions

Step: 1

1 week = 7 days.

Step: 2

Number of days in n weeks = n × number of days in a week = n × 7 = 7n.

Step: 3

The variable expression for this situation is 7n.

Correct Answer is : 7n

Q4The amount of orange juice present in a pitcher is 1 liter less than twice the amount of juice present in the other pitcher. Choose an algebraic expression to represent this situation.
A. 2 + n - 1
B. n2 - 1
C. 2n + 1
D. 2n - 1

Solutions

Step: 1

Twice of an amount of juice will be equal to 2 × n or 2n.

Step: 2

One liter less than this amount will be equal to 2n - 1.

Step: 3

2n - 1 is the correct answer.

Correct Answer is : 2n - 1

Q5The amount of sugar present in a jar is 10g less than twice the amount of sugar present in the other jar. Choose an algebraic expression to represent this situation.
A. 2n - 10
B. 2 + n - 10
C. 2n + 10
D. n2 - 10

Solutions

Step: 1

Twice of an amount of sugar will be equal to 2 × n or 2n.

Step: 2

Ten grams less than this amount will be equal to 2n - 10.

Step: 3

2n-10 is the correct answer.

Correct Answer is : 2n - 10

Q6Lindsay's salary was $y 3 years ago. Now, she gets 4 times her previous salary and she spends $1512. Calculate her savings.

A. $(1512 + 4y)
B. $(1512 - y)
C. $(1512 - 4y)
D. $(4y - 1512)

Solutions

Step: 1

Lindsay's present salary is $4y.

Step: 2

Lindsay's savings = $(4y - 1512)

[Savings = Income - Expenditure.]

Correct Answer is : $(4y - 1512)

Q7Paul and Matt fire 46 shots each to hit a target. Each person gets p points for a hit and loses q points for a miss. Paul hits the mark 40 times and Matt hits the mark 38 times. Identify the variable expressions for their individual scores.

A. 40p - 6, 38p - 8
B. 40p, 38q
C. 40p - 6q, 38p - 8q
D. 38p, 40q

Solutions

Step: 1

Points scored by each person = Number of hits × p - Number of missed hits × q

Step: 2

Number of hits that Paul missed = (46 - 40) = 6

[Subtract.]

Step: 3

The variable expression for the points scored by Paul is 40p - 6q.

Step: 4

Number of hits that Matt missed = (46 - 38) = 8

[Subtract.]

Step: 5

The variable expression for the points scored by Matt is 38p - 8q.

Step: 6

So, the variable expressions for the points scored by Paul and Matt are 40p - 6q and 38p - 8q.

Correct Answer is : 40p - 6q, 38p - 8q

Q8Which of the following is the correct choice for the statement, "y is divided by a number 38"?

A. y - 38
B. y + 38
C. y38
D. 38y

Solutions

Step: 1

y is divided by a number 38.

[In words.]

Step: 2

y38

[Variable expression.]

Step: 3

Variable expression for the word phrase is y38.

Correct Answer is : y38

Q9Which of the following choices represents the phrase "3 added to 5 times x is equal to 19"?

A. 5x - 3 = 19
B. 5(x + 3) = 19
C. x3 + 3 = 19
D. 3 + 5x = 19

Solutions

Step: 1

5 times x = 5x

Step: 2

3 added to 5x = 3 + 5x

[Add 3 to 5x.]

Step: 3

3 added to 5 times x is equal to 19 is 3 + 5x = 19.

Correct Answer is : 3 + 5x = 19

Q10Choose an algebraic sentence for " Seven times the quantity of a number decreased by ten is equal to 186 more than the number". Let c be the number.

A. 7(c - 10) = 186 + c
B. 7(c - 10) > 186
C. 7c - 10 = 186c
D. 7c + 10 = 186 + c

Solutions

Step: 1

Seven times the quantity of a number decreased by ten = 7(c - 10).

Step: 2

186 more than the number = 186 + c.

Step: 3

The algebraic sentence for the given word sentence: 7(c - 10) = 186 + c.

Correct Answer is : 7(c - 10) = 186 + c

Q11Which of the following choices represents the word phrase "4 added to 4 times x is equal to 19"?

A. x4 + 4 = 19
B. 4(x + 4) = 19
C. 4 + 4x = 19
D. 4x - 4 = 19

Solutions

Step: 1

4 times x = 4x

Step: 2

4 added to 4x = 4 + 4x

[Add 4 to 4x.]

Step: 3

4 added to 4 times x is equal to 19 is 4 + 4x = 19

Correct Answer is : 4 + 4x = 19

Q12Choose the graph for the inequality, | w + 52 | - 4 > 5.

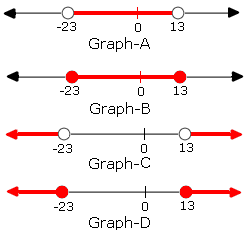
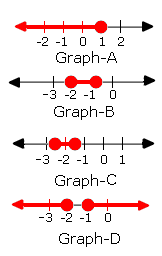
A. Graph A
B. Graph B
C. Graph C
D. Graph D

Solutions

Step: 1

| w + 52 | - 4 > 5

Step: 2

| w + 52 | > 9

Step: 3

w + 5 2 > 9 or w + 52 < -9

[Write the equivalent disjunction.]

Step: 4

(w + 5) > 18 or (w + 5) < -18

[Multiply throughout by 2.]

Step: 5

w > 13 or w < - 23

Step: 6

The solution set is {w: w < - 23 or w > 13}

Step: 7

The graphical representation is as follows:

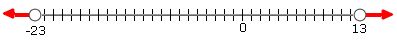
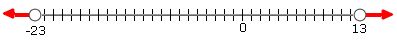
Correct Answer is : Graph C

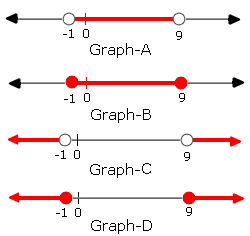
Q13Choose the graph for the inequality, 5 < | x - 4 |.

A. Graph A
B. Graph B
C. Graph C
D. Graph D

Solutions

Step: 1

5 < | x - 4 |

Step: 2

5 < (x - 4) or - 5 > (x - 4)

[Write the equivalent disjunction.]

Step: 3

9 < x or - 1 > x

Step: 4

That is x < - 1 or x > 9

Step: 5

The solution set is {x: x < - 1 or x > 9}

Step: 6

The graphical representation is as follows:

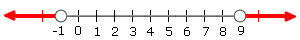
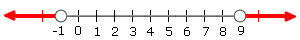
Correct Answer is : Graph C

Q14Choose the graph for the inequality, | 5 + 2(x - 1) | ≤ 1.

A. Graph B
B. Graph A
C. Graph D
D. Graph C

Solutions

Step: 1

| 5 + 2(x - 1) | ≤1

Step: 2

5 + 2(x - 1) ≤ 1 and 5 + 2(x -1) ≥ - 1

Step: 3

2(x - 1) ≤- 4 and 2(x - 1) ≥ - 6

[Subtracting 5 from the two sides of the equation.]

Step: 4

(x - 1) ≤- 2 and (x - 1) ≥ - 3

[Divide throughout by 2.]

Step: 5

x ≤ - 1 and x ≥ - 2

[Add 1 to both sides of the equation.]

Step: 6

The solution set is {x: - 2 ≤ x ≤- 1}

Step: 7

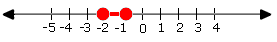
Correct Answer is : Graph B

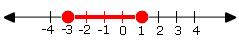
Q15Choose an inequality for the graph shown.

A. | x + 1 | ≤ 2
B. | x + 1 | ≥ 2
C. | x + 1 | > 2
D. | x + 1 | < 2

Solutions

Step: 1

The graph shows the values between - 3 and 1 including the points -3, 1.

Step: 2

-3 ≤ x ≤ 1

Step: 3

-2 ≤ x + 1 ≤ 2

[Add 1 throughout.]

Step: 4

| x + 1 | ≤ 2

Correct Answer is : | x + 1 | ≤ 2

Solved Examples and Worksheet for Solving and Graphing Absolute Value Inequalities

Related Worksheet

Related Topic

HighSchool Math