Solved Examples and Worksheet for Solving Systems of Equations Graphically
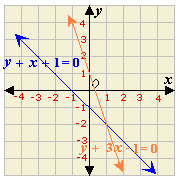
A. (2, 1)
B. (1, 2)
C. (1, - 2)
D. (- 1, - 2)
Step: 1
The two lines appear to intersect at the point (1, - 2).
Step: 2
Check the solution algebraically:y x
[Equation 1.]
Step: 3
(- 2) + 1 + 1 = 0
[Substitute x y
Step: 4
0 = 0
[Simplify.]
Step: 5
[Equation 2.]
Step: 6
- 2 + 3(1) - 1 = 0
[Substitute x y
Step: 7
0 = 0
[Simplify.]
Step: 8
The ordered pair (1, - 2) satisfies both the equations.
Step: 9
So, (1, - 2) is the solution of the linear system.
Correct Answer is : (1, - 2)
A. Infinitely many solutions
B. No solution
C. Exactly one solution
D. Two solutions
Step: 1
- 2x y
Step: 2
- 10x y
Step: 3
Dividing Equation (2) by 5, we get - 2x y
Step: 4
Graph the equations.
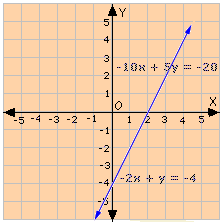

Step: 5
Both the equations represent the same line. So, each point on the line is a solution of the system.
Step: 6
So, the pair of equations has infinitely many solutions.
Correct Answer is : Infinitely many solutions
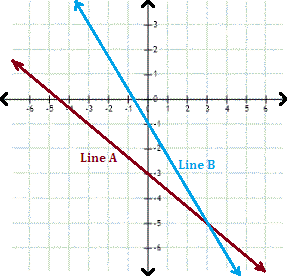
A. 2
B. 2
C. 2
D. 2
Step: 1
From the graph, the y
Step: 2
Slope of the line A = - 3 - ( - 5 ) 0 - 3 2 3
[Line A passes through (0, -3) and (3, -5)]
Step: 3
The equation of the line A is y 2 3 x x y
[Slope-intercept form of a line is y = mx + b, where m is the slope and b is the y-intercept.]
Step: 4
From the graph, the y
Step: 5
Slope of the line B = - 1 - ( - 5 ) 0 - 3 4 3
[Line B passes through (0, - 1) and (3, -5)]
Step: 6
The equation of the line B is y 4 3 x x y
[Slope-intercept form of a line is y mx + b m b y
Step: 7
Therefore, the linear system represented by the graph is 2x y x y
Correct Answer is : 2x y x y
2
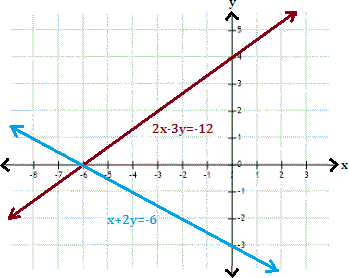
A. (-5, 0)
B. (-6, 0)
C. None of these
D. (0, -6)
Step: 1
The graphs represented by the given system of equations appear to intersect at (-6, 0). Therefore, the solution is (-6, 0).
Step: 2
Check the solution algebraically by substituting x y
Step: 3
2x y
[Substitute x y
Step: 4
[Substitute x y
Step: 5
The ordered pair (-6, 0) satisfies both the equations. Hence, (-6, 0) is the solution of the given linear system.
Correct Answer is : (-6, 0)
2
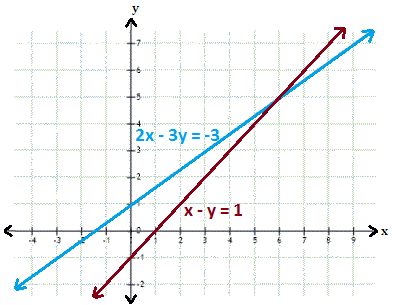
A. (6, 5)
B. (6, 6)
C. (5, 5)
D. (5, 6)
Step: 1
The graphs represented by the given system of equations appear to intersect at (6, 5). Therefore, the solution is (6, 5).
Step: 2
Check the solution algebraically by substituting x y
Step: 3
[Substitute x y
Step: 4
2x y
[Substitute x y
Step: 5
The ordered pair (6, 5) satisfies both the equations. Hence, (6, 5) is the solution of the given linear system.
Correct Answer is : (6, 5)
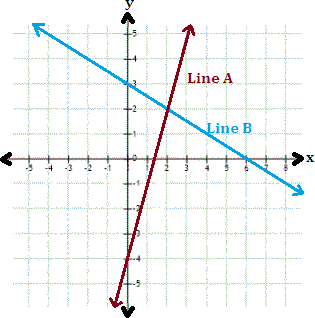
A. 3
B. 3
C. 3
D. 3
Step: 1
From the graph, the y
Step: 2
Slope of the line A = - 4 - 2 0 - 2
[Line A passes through (0, - 4) and (2, 2)]
Step: 3
The equation of the line A is y x x y
[Slope-intercept form of a line is y = mx + b y
Step: 4
From the graph, the y
Step: 5
Slope of the line B = 3 - 2 0 - 2 1 2
[Line B passes through (0, 3) and (2, 2)]
Step: 6
The equation of the line B is y 1 2 x x y
[Slope-intercept form of a line is y = mx + b y
Step: 7
Therefore, the linear system represented by the graph is 3x y x y
Correct Answer is : 3x y x y
3
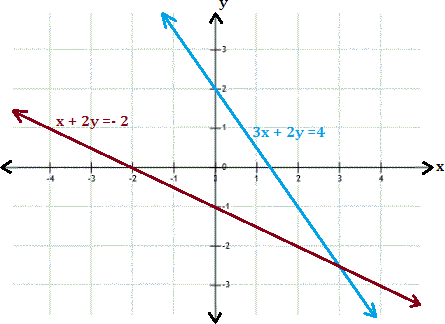
A. (3,
B. (2, -
C. (3, -
D. ( - 3, -
Step: 1
The graphs represented by the given system of equations appear to intersect at (3, - 5 2 5 2
Step: 2
Check the solution algebraically by substituting x = 3 and y = - 5 2
Step: 3
[substitute x y 5 2
Step: 4
3x y 5 2
[Substitute x y 5 2
Step: 5
The ordered pair (3, - 5 2 5 2
Correct Answer is : (3, - 5 2
2
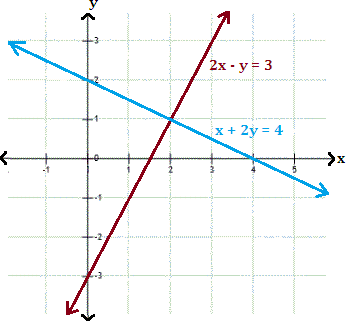
A. (0, 2)
B. (2, 1)
C. (0, -3)
D. (2, 2)
Step: 1
The graphs represented by the given system of equations appear to intersect at (2, 1). Therefore, the solution is (2, 1).
Step: 2
Check the solution algebraically by substituting x y
Step: 3
2x y
[Substitute x y
Step: 4
[Substitute x y
Step: 5
The ordered pair (2, 1) satisfies both the equation. Hence, (2, 1) is the solution of the given linear system.
Correct Answer is : (2, 1)
2
2
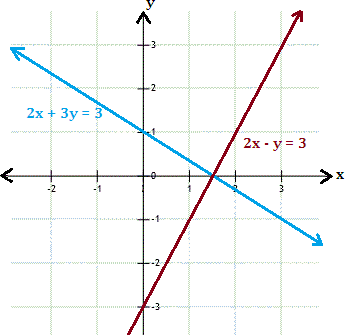
A. (
B. (0, -3)
C. (-3, 0)
D. (0,
Step: 1
The graphs represented by the given system of equations appear to intersect at (3 2 3 2
Step: 2
Check the solution algebraically by substituting x 3 2 y
Step: 3
2x y 3 2
[Substitute x 3 2 y
Step: 4
2x y 3 2
[Substitute x 3 2 y
Step: 5
The ordered pair (3 2 3 2
Correct Answer is : (3 2
- Solving One-Step Linear Equations-Algebra1-Solved Examples
- Solving Two-Step Linear Equations-Algebra1-Solved Examples
- Solving One-Step Linear Inequalities-Algebra1-Solved Examples
- Graphing Linear Equations and Inequalities-Algebra1-Solved Examples
- Solving and Graphing Absolute Value Equations-Algebra1-Solved Examples
- Solving and Graphing Absolute Value Inequalities-Algebra1-Solved Examples
- Identifying the Graph for the Table-Algebra1-Solved Examples
- Solving Systems of Equations using Elimination Method-Algebra1-Solved Examples
- Solving Systems of Equations using Substitution Method-Algebra1-Solved Examples
- Graphing Systems of Equations and Inequalities-Algebra1-Solved Examples
- Solving Quadratic Equations By Completing Squares-Algebra1-Solved Examples
- Solving Quadratic Equations by Finding Square Roots-Algebra1-Solved Examples
- No real Solutions for Quadratic Equations-Algebra1-Solved Examples
- Solving Quadratic Equations Graphically-Algebra1-Solved Examples
- Solving Quadratic Linear Systems of Equations-Algebra1-Solved Examples
Related Worksheet
- System Of Equations