Solved Examples and Worksheet for Graphing Systems of Equations and Inequalities
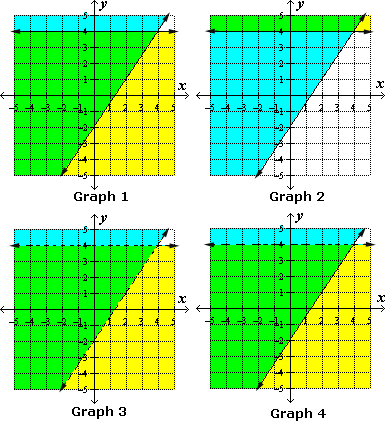
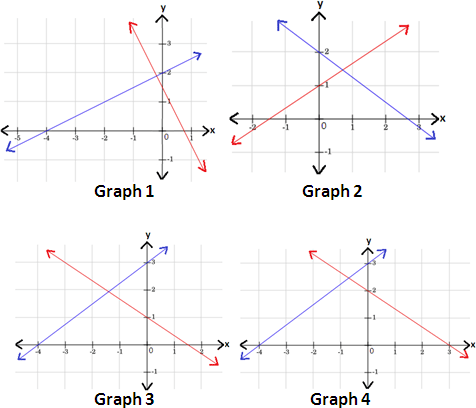
A. Graph 4
B. Graph 3
C. Graph 2
D. Graph 1
Step: 1
The graph of y y
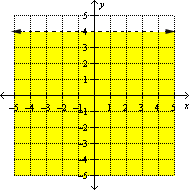

Step: 2
The graph of y 3 2 x y 3 2 x
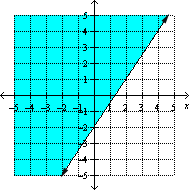

Step: 3
Graph both the inequalities in the same coordinate plane. The graph of the system is the overlap or intersection of the two half-planes shown as green color.
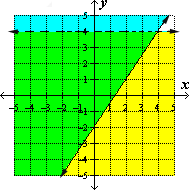

Correct Answer is : Graph 4
4
2
A. Graph 4
B. Graph 2
C. Graph 1
D. Graph 3
Step: 1
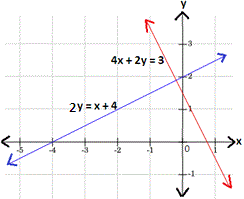
Write each equation in slope-intercept form y = mx + b m b y
Step: 2
4x y y x y x 3 2
Step: 3
2y x y 1 2 x
Step: 4
Graph the two equations using the slope and y

Step: 5
Therefore, graph 1 represents the given system of linear equations.
Correct Answer is : Graph 1
2
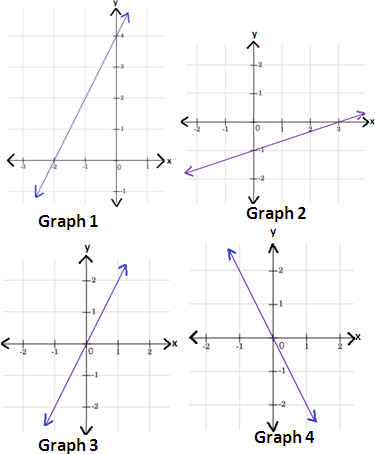
A. Graph 4
B. Graph 2
C. Graph 3
D. Graph 1
Step: 1
Write each equation in slope-intercept form y = mx + b m b y
Step: 2
Step: 3
2x y y x y 1 3 x
Step: 4
Graph the two equations using the slope and y

Step: 5
Therefore, graph 2 represents the given system of linear equations.
Correct Answer is : Graph 2
2
6
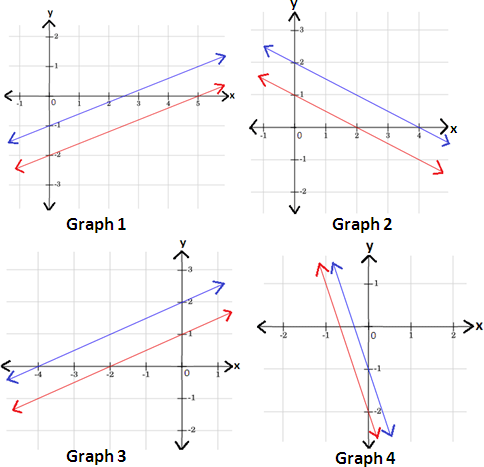
A. Graph 3
B. Graph 1
C. Graph 2
D. Graph 4
Step: 1
Write each equation in slope-intercept form y = mx + b b y
Step: 2
2x y y x y 2 5 x
Step: 3
6x y y x y 2 5 x
Step: 4
Graph the two equations using the slope and y
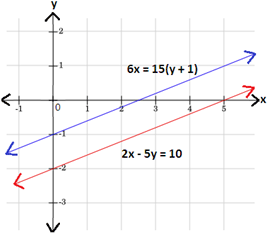

Step: 5
Therefore, graph 1 represents the given system of linear equations.
Correct Answer is : Graph 1
-5
6
A. Graph 3
B. Graph 4
C. Graph 2
D. Graph 1
Step: 1
Write each equation in slope-intercept form y = mx + b m b y
Step: 2
- 5x y y x y 5 6 x 4 3
Step: 3
6x y y x y 3 4 x
Step: 4
Graph the two equations using the slope and y

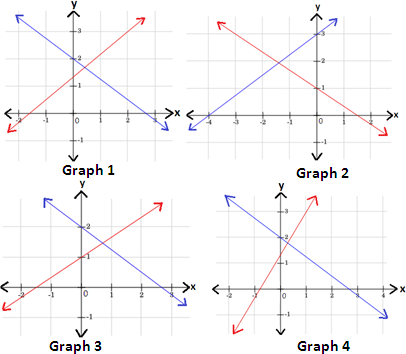
Step: 5
Therefore, graph 1 represents the given system of linear equations.
Correct Answer is : Graph 1
3
- 9

A. Graph 2
B. Graph 4
C. Graph 1
D. Graph 3
Step: 1
Write each equation in slope-intercept form y = mx + b m b y
Step: 2
3x y y x y 3 2 x
Step: 3
- 9x y y x y 3 2 x
Step: 4
Graph the two equations using the slope and y
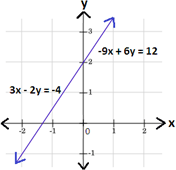

Step: 5
Therefore, graph 4 represents the given system of linear equations.
Correct Answer is : Graph 4
6
9
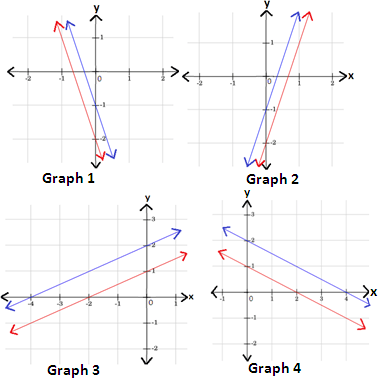
A. Graph 3
B. Graph 4
C. Graph 2
D. Graph 1
Step: 1
Write each equation in slope-intercept form y = mx + b m b y
Step: 2
6x y y x y x
Step: 3
9x y y x y x
Step: 4
Graph the two equations using the slope and y-intercept.

Step: 5
Therefore, graph 2 represents the given system of linear equations.
Correct Answer is : Graph 2
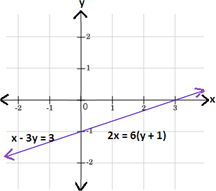
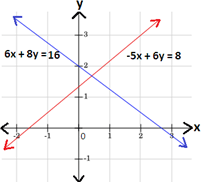
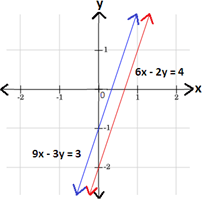
5x - 6y = 6
-3x + 2y = 2
A. Graph 3
B. Graph 4
C. Graph 1
D. Graph 2
Step: 1
Write each equation in slope-intercept form y = mx + b m b y
Step: 2
5x y y x y 5 6 x
Step: 3
- 3x y y x y 3 2 x
Step: 4
Graph the two equations using the slope and y
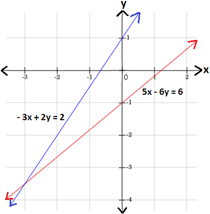

Step: 5
Therefore, graph 4 represents the given system of linear equations.
Correct Answer is : Graph 4
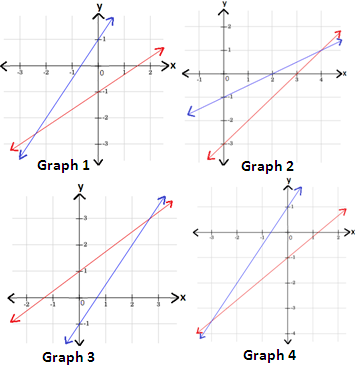
3
4
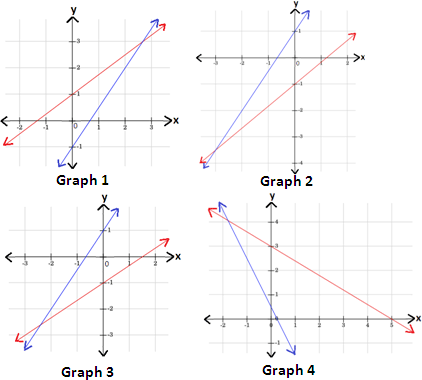
A. Graph 1
B. Graph 3
C. Graph 4
D. Graph 2
Step: 1
Write each equation in slope-intercept form y = mx + b m b y
Step: 2
3x y y x y 3 5 x
Step: 3
4x y y x y x 1 2
Step: 4
Graph the two equations using the slope and y
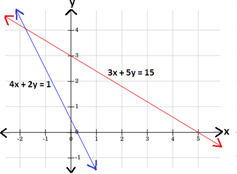

Step: 5
Therefore, graph 4 represents the given system of linear equations.
Correct Answer is : Graph 4
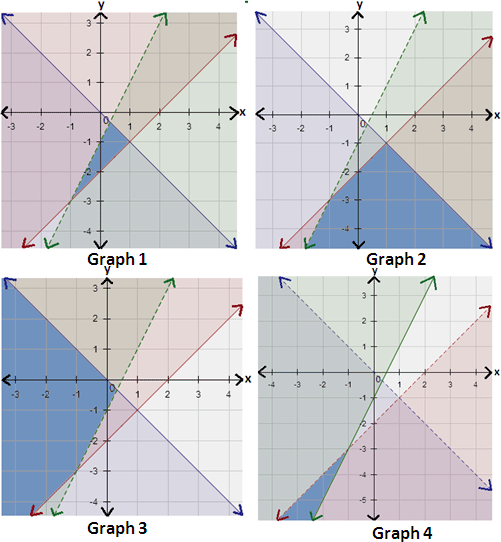
A. Graph 2
B. Graph 1
C. Graph 4
D. Graph 3
Step: 1
The boundary of the half - plane is dashed if the inequality is < or > and solid if the inequality is ≤ or ≥.
Step: 2
The graph of x y x y
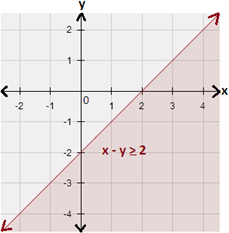

Step: 3
The graph of x y x y
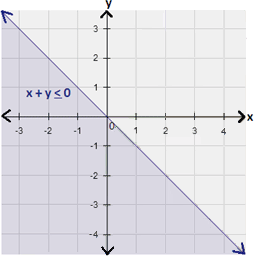

Step: 4
The graph of 2x y x y
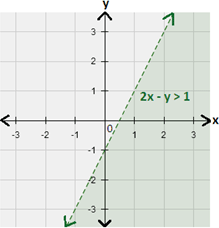

Step: 5
Graph all inequalities in the same coordinate plane. The graph of the system is the overlap, or intersection, of the three half-planes as shown below.
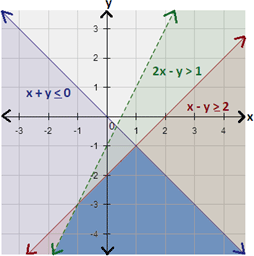

Correct Answer is : Graph 2
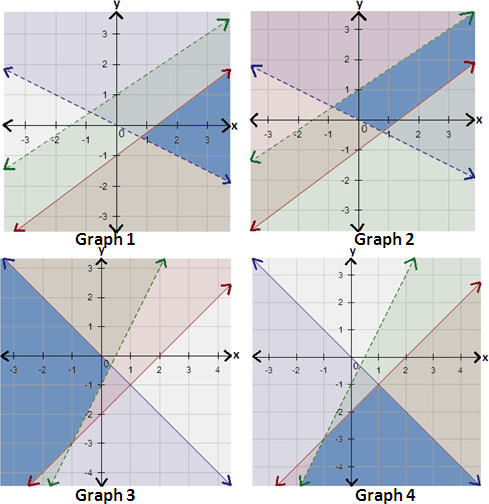
A. Graph 3
B. Graph 2
C. Graph 4
D. Graph 1
Step: 1
The boundary line of the half - plane is dashed if the inequality is < or > and solid if the inequality is ≤ or ≥.
Step: 2
The graph of 3x y x y
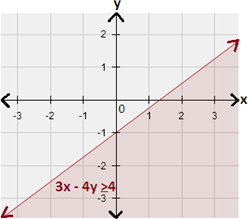

Step: 3
The graph of x y x y
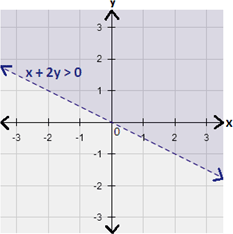

Step: 4
The graph of - 2x y x y
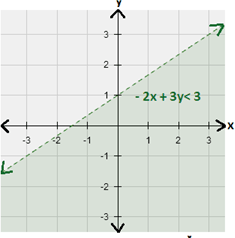

Step: 5
Graph all inequalities in the same coordinate plane. The graph of the system is the overlap, or intersection, of the three half-planes as shown below.
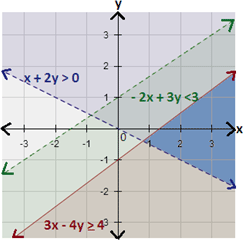

Correct Answer is : Graph 1
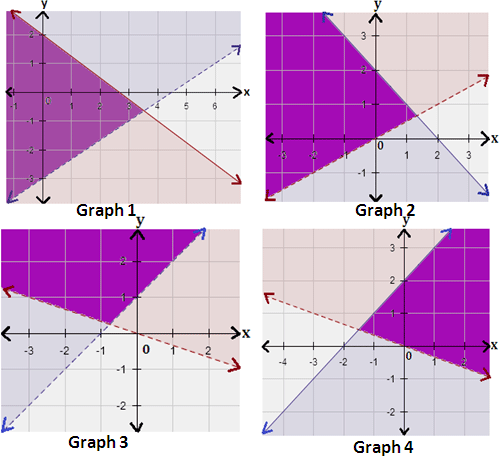
A. Graph 4
B. Graph 2
C. Graph 3
D. Graph 1
Step: 1
The boundary line of the half-plane is dashed if the inequality is < or > and solid if the inequality is ≤ or ≥.
Step: 2
The graph of 3x y x y
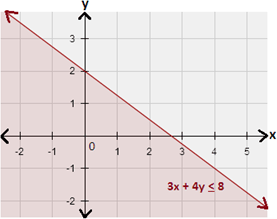

Step: 3
The graph of 2x y x y
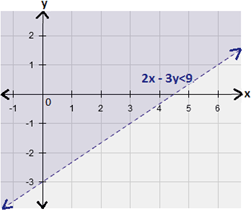

Step: 4
Graph the two inequalities in the same coordinate plane. The graph of the system is the overlap, or intersection, of the two half-planes as shown below.
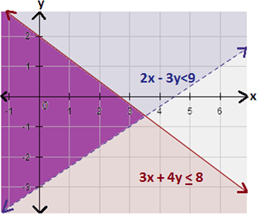

Correct Answer is : Graph 1
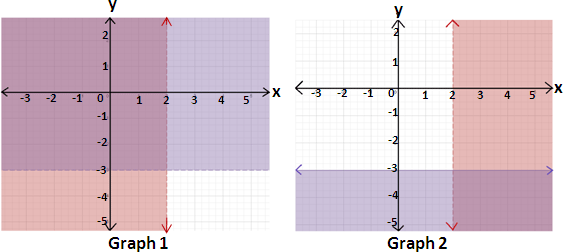
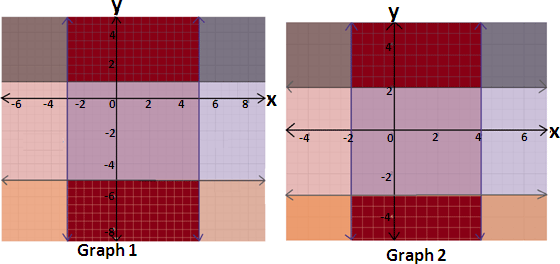
A. Graph 1
B. Graph 2
Step: 1
The boundary line of the half-plane is dashed if the inequality is < or > and solid if the inequality is ≤ or ≥.
Step: 2
The graph of x x
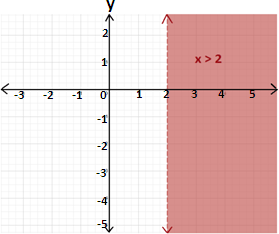
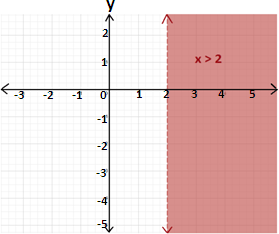
Step: 3
The graph of y y
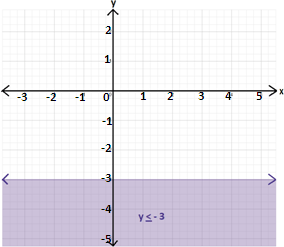

Step: 4
Graph the two inequalities in the same coordinate plane. The graph of the system is the overlap, or intersection, of the two half-planes as shown below.
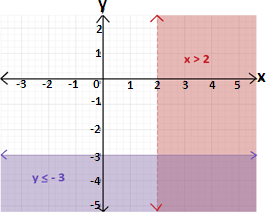

Correct Answer is : Graph 2
A. Graph 2
B. Graph 1
Step: 1
|x
[First inequality.]
Step: 2
⇒ x x
Step: 3
⇒ x x x x
[Add 1 to both sides of the inequality.]
Step: 4
The graph of x x x x

Step: 5
|y
[Second inequality.]
Step: 6
⇒ y y
Step: 7
⇒ y y y y
[Subtract 2 from both sides of the inequality.]
Step: 8
The graph of y y y y
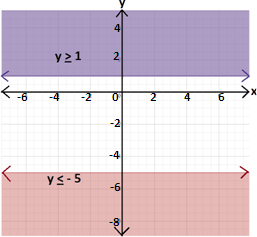

Step: 9
Combine the two given inequalities. The solution of the given system includes all points on or above y x x y x x
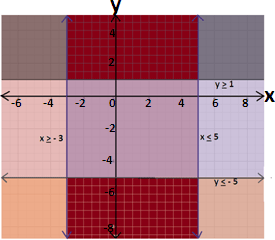

Correct Answer is : Graph 1
- Solving One-Step Linear Equations-Algebra1-Solved Examples
- Solving Two-Step Linear Equations-Algebra1-Solved Examples
- Solving One-Step Linear Inequalities-Algebra1-Solved Examples
- Graphing Linear Equations and Inequalities-Algebra1-Solved Examples
- Solving and Graphing Absolute Value Equations-Algebra1-Solved Examples
- Solving and Graphing Absolute Value Inequalities-Algebra1-Solved Examples
- Identifying the Graph for the Table-Algebra1-Solved Examples
- Solving Systems of Equations using Elimination Method-Algebra1-Solved Examples
- Solving Systems of Equations using Substitution Method-Algebra1-Solved Examples
- Solving Systems of Equations Graphically-Algebra1-Solved Examples
- Solving Quadratic Equations By Completing Squares-Algebra1-Solved Examples
- Solving Quadratic Equations by Finding Square Roots-Algebra1-Solved Examples
- No real Solutions for Quadratic Equations-Algebra1-Solved Examples
- Solving Quadratic Equations Graphically-Algebra1-Solved Examples
- Solving Quadratic Linear Systems of Equations-Algebra1-Solved Examples
Related Worksheet
- Coordinate Plane
- Graph
- System Of Inequalities