Solved Examples and Worksheet for Solving Quadratic Equations By Completing Squares

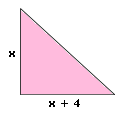
Q1The area of the right triangle is 48 square cm. What is the value of x?


A. 8
B. 6
C. 13
D. 10

Solutions
Share 
Step: 1
The area of a right triangle is given by, A = 12 x base x height
Step: 2
48 = 12 x (x + 4) x x
  [Substitute 48 for A, x for height and (x + 4) for base.]
Step: 3
48 x 2 = 12x (x + 4) x x x 2
  [Multiply each side by 2.]
Step: 4
96 = x (x + 4)
  [Simplify.]
Step: 5
96 = x2 + 4x
  [Use distributive property.]
Step: 6
96 + 22 = x2 + 4x + 22
  [To make RHS a perfect square, add (4/2)2 = (2)2 to each side.]
Step: 7
100 = (x + 2)2
  [Write right side as a perfect square.]
Step: 8
± 10 = (x + 2)
  [Find square roots on each side.]
Step: 9
x = ±10 - 2
  [Subtract 2 from each side.]
Step: 10
x = 8
  [Since x is the height of the triangle, discard the negative value.]
Correct Answer is :   8
Q2Solve x2 + 8x = 33 by completing the square.

A. 8 and 33
B. 1 and - 33
C. - 11 and 3
D. - 11 and - 3

Solutions
Share 
Step: 1
x2 + 8x = 33
  [Original equation.]
Step: 2
x2 + 8x + 42 = 33 + 42
  [Add ( 82)2 = 42 to each side.]
Step: 3
(x + 4)2 = 49
  [Writing left side as perfect square.]
Step: 4
(x + 4) = ± 7
  [Finding square roots on each side.]
Step: 5
x = - 4 ± 7
  [Subtract 4 from each side.]
Step: 6
x = - 11 or x = 3
  [Simplify.]
Step: 7
The solutions of the equation x2 + 8x = 33 are - 11 and 3.
Correct Answer is :   - 11 and 3
Q3Solve x2 - 10x = 11 by completing the square.

A. - 11 and - 1
B. 11 and - 5
C. 13 and - 1
D. 11 and - 1

Solutions
Share 
Step: 1
x2 - 10x = 11
  [Original equation.]
Step: 2
x2 - 10x + 25 = 11 + 25
  [Add (- 102)2 = (- 5)2 = 25 to each side.]
Step: 3
(x - 5)2 = 36
  [Write left side as perfect square and simplify.]
Step: 4
x - 5 = ± 6
  [Evaluate square roots on both sides.]
Step: 5
x = 5 ± 6
  [Add 5 to each side.]
Step: 6
x = 11 or x = - 1
  [Simplify.]
Step: 7
The solutions of the equation x2 - 10x = 11 are 11 and - 1.
Correct Answer is :   11 and - 1
Q4Solve the quadratic equation by completing the square.
- 2x2 + 20x = - 18

A. 4 ± 34
B. 5 ± 34
C. 6 ± 34
D. 7 ± 34

Solutions
Share 
Step: 1
- 2x2 + 20x = - 18
Step: 2
⇒ x2 - 10x = 9
  [Divide throughout by - 2.]
Step: 3
x2 - 10x + 25 = 9 + 25
  [Add (- 102)2 = (- 5)2 = 25 to both sides of the equation.]
Step: 4
(x - 5)2 = 34
  [Write left side as perfect square and simplify.]
Step: 5
(x - 5) = ± 34
  [Find the square root of both sides.]
Step: 6
x = 5 ± 34
  [Add 5 to both sides of the equation.]
Step: 7
x = 5 + 34 or x = 5 - 34
Step: 8
The solutions of the equation - 2x2 + 20x = - 18 are x = 5 + 34 and x = 5 - 34.
Correct Answer is :   5 ± 34
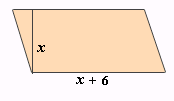
Q5The area of the parallelogram 27 cm2. What is its length?

A. 8 cm
B. 7 cm
C. 9 cm
D. 6 cm

Solutions
Share 
Step: 1
The area of a parallelogram is equal to the product of its height and length.
Step: 2
27 = x(x + 6)
  [Original equation.]
Step: 3
27 = x2 + 6x
  [Use distributive property to simplify.]
Step: 4
27 + 32 = x2 + 6x + 32
  [Add (62)2 = (3)2 = 9 to each side.]
Step: 5
36 = (x + 3)2
  [Write right side as a perfect square and simplify.]
Step: 6
± 6 = (x + 3)
  [Evaluate square roots on both sides.]
Step: 7
x = ± 6 - 3
  [Subtract 3 from each side.]
Step: 8
x = 3 or - 9
  [Simplify.]
Step: 9
Height of the parallelogram is x = 3 cm.
  [Since height cannot be a negative value.]
Step: 10
Length = x + 6 = 3 + 6 = 9 cm
  [Simplify.]
Correct Answer is :   9 cm
Q6Solve the quadratic equation.
x2 + 10x + 3 = 0

A. - 5 + 22
B. 5 ± 22
C. - 5 ± 22
D. - 5 - 26

Solutions
Share 
Step: 1
x2 + 10x + 3 = 0
  [Given.]
Step: 2
x2 + 10x = - 3
  [Subtract 3 from both sides.]
Step: 3
x2 + 10x +(5)2 = - 3 + (5)2
  [Add (102)2 or 52 to each side.]
Step: 4
(x + 5)2 = 22
  [Factor left side.]
Step: 5
x + 5 = ± 22
Step: 6
x = - 5 ± 22
Correct Answer is :   - 5 ± 22
Q7Solve:
x2 - 10x - 6 = 0
A. - 5, 5
B. - 5 ± 31
C. 36, - 26
D. 5 ± 31

Solutions
Share 
Step: 1
x2 - 10x - 6 = 0
  [Given.]
Step: 2
x2 - 10x = 6
  [Add 6 to both sides.]
Step: 3
x2 - 10x + 52 = 6 + 52
  [Add (- 102)2 or 52 to each side.]
Step: 4
(x - 5)2 = 31
Step: 5
x - 5 = ± 31
Step: 6
x = 5 ± 31
Correct Answer is :   5 ± 31
Q8Solve the quadratic equation by completing the square.
x2 + 16x + 307 = 0

A. - 8 ± 93i
B. - 64 ± 93i
C. - 8 ± 93
D. - 8 ± 813i

Solutions
Share 
Step: 1
x2 + 16x + 307 = 0
  [Original equation.]
Step: 2
⇒ x2 + 16x = - 307
  [Subtracting 307 from the two sides of the equation.]
Step: 3
x2 + 16x + 64 = - 307 + 64
  [Add (162)2 = (8)2 = 64 to both sides of the equation.]
Step: 4
(x + 8)2 = - 243
  [Write left side as perfect square and simplify.]
Step: 5
(x + 8) = ±(- 243)
  [Find the square root of both sides.]
Step: 6
(x + 8) = ± 93i
  [(-243) = 243i2 = 93i.]
Step: 7
x = - 8 ± 93i
  [Subtracting 8 from the two sides of the equation.]
Step: 8
x = - 8 + 93i or x = - 8 - 93i
Step: 9
The solutions of the equation x2 + 16x + 307 = 0 are x = - 8 + 93i and x = - 8 - 93i.
Correct Answer is :   - 8 ± 93i
Q9Solve the quadratic equation by completing the square.
- m2 - 8m = 32

A. - 4 ± 4i
B. 4 - 4i
C. 0 and - 4
D. 4 + 4i

Solutions
Share 
Step: 1
- m2 - 8m = 32
  [Original equation.]
Step: 2
⇒ m2 + 8m = - 32
  [Multiply throughout by - 1.]
Step: 3
m2 + 8m + 16 = - 32 + 16
  [Add (82)2 = (4)2 = 16 to both sides of the equation.]
Step: 4
(m + 4)2 = - 16
  [Write left side as perfect square and simplify.]
Step: 5
(m + 4) = ± (-16)
  [Find the square root of both sides.]
Step: 6
(m + 4) = ± 4i
  [(-16) = (4i)2 = 4i.]
Step: 7
m = - 4 ± 4i
  [Subtracting 4 from the two sides of the equation.]
Step: 8
m = - 4 + 4i or m = - 4 - 4i
Step: 9
The solutions of the equation - m2 - 8m = 32 are m = - 4 + 4i and m = - 4 - 4i.
Correct Answer is :   - 4 ± 4i
Q10Solve the quadratic equation by completing the square.
x2 + 6x - 15 = 0.
A. - 2 ± 26
B. - 3 ± 2 6
C. 2 ± 6
D. - 3 ± 6

Solutions
Share 
Step: 1
x2 + 6x - 15 = 0
  [Given.]
Step: 2
x2 +6x = 15
  [Add 15 to both sides.]
Step: 3
x2 + 6x + 3 2 = 15 + 3 2
  [Add ( -62)2 or 3 2 to each side.]
Step: 4
(x + 3)2 = 24
  [Writing left side as perfect square.]
Step: 5
x +3 = ± 24
  [Square root property.]
Step: 6
x = - 3 ± 24
Step: 7
x = - 3 ± 2 6
  [Simplify.]
Correct Answer is :   - 3 ± 2 6

HighSchool Math