Solved Examples and Worksheet for Solving Quadratic Equations Graphically

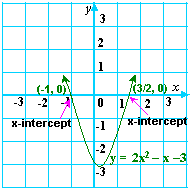
Q1Estimate the solution of 2x2 - x = 3 using the graph.


A. 1 and -2
B. 2 and 8
C. -1 and 3
D. -1 and 32

Solutions
Share 
Step: 1
From the figure, the graph intersects the x - axis at two points (-1, 0) and ( 32, 0).
Step: 2
The x-intercepts of the curve are -1 and 32.
Step: 3
2x2 - x = 3
  [Original equation]
Step: 4
2(-1)2 - (-1) = 3
  [Substitute x-intercept as -1.]
Step: 5
3 = 3
  [Simplify.]
Step: 6
2( 32)2 - (32) = 3
  [Substitute x-intercept as 32.]
Step: 7
3 = 3
  [Simplify.]
Step: 8
Both the values satisfy the equation. So, -1 and 32 are the solutions of the equation.
Correct Answer is :   -1 and 32
Q2Find the solution of - 3x2 = - 27 using a graph.
A. - 3 and 6
B. - 3 and 7
C. - 4 and 4
D. - 3 and 3

Solutions
Share 
Step: 1
- 3x2 = - 27
  [Original equation]
Step: 2
x2 = 9
  [Divide - 3 on each side]
Step: 3
x2 - 9 = 9 - 9
  [Subtract 9 from each side]
Step: 4
x2 - 9 = 0
  [Simplify.]
Step: 5
Sketch the graph of the related quadratic function y = x2 - 9 as shown below.
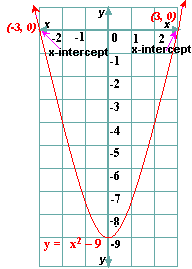
Step: 6
From the graph, the x-intercepts appear to be - 3 and 3.
  [Estimate the values of the x-intercepts.]
Step: 7
So, - 3 and 3 are the solutions of the equation.
Correct Answer is :   - 3 and 3
Q3A rectangular fountain in a park has dimensions of a and a + 16. If the area of the fountain is 192 square meters, find the dimensions of the fountain in meters.
A. 9, 25
B. 11, 27
C. 8, 24
D. 10, 26

Solutions
Share 
Step: 1
The area of a rectangle = length × width.
Step: 2
The area of the rectangular fountain = (a) × (a + 16) square meters.
Step: 3
192 = (a) × (a + 16)
  [Original equation.]
Step: 4
192 = a2 + 16a
  [Use distributive property.]
Step: 5
192 + 82 = a2 + 16a + 82
  [Add (162)2 = 82 = 64 to each side.]
Step: 6
256 = (a + 8)2
  [Write the right hand side as a perfect square and simplify.]
Step: 7
± 16 = a + 8
  [Evaluate square roots on both sides.]
Step: 8
± 16 - 8 = a + 8 - 8
  [Subtract 8 from each side.]
Step: 9
a = + 8 or - 24
  [Simplify.]
Step: 10
Width = a = 8 meters
  [The dimensions cannot be negative.]
Step: 11
Length = (a + 16) = (16 + 8) = 24 meters.
  [Substitute 8 for a and add.]
Step: 12
The dimensions of the fountain are 8 meters wide and 24 meters long.
Correct Answer is :   8, 24
Q4The area of a rectangular book is 364 square centimeters. If its dimensions are a and a + 12, find the length and width of the book.
A. 16 cm, 28 cm
B. 14 cm, 26 cm
C. 15 cm, 27 cm
D. 13 cm, 25 cm

Solutions
Share 
Step: 1
The area of a rectangle = length × width.
Step: 2
The area of the rectangular book = (a) × (a + 12) square centimeters.
Step: 3
364 = (a) × (a + 12)
  [Original equation.]
Step: 4
364 = a2 + 12a
  [Use distributive property.]
Step: 5
364 + 62 = a2 + 12a + 62
  [Add (122)2 = 62 = 36 to each side.]
Step: 6
400 = (a + 6)2
  [Write the right hand side as a perfect square and simplify.]
Step: 7
± 20 = (a + 6)
  [Evaluate square roots on both sides.]
Step: 8
± 20 - 6 = a + 6 - 6
  [Subtract 6 from each side.]
Step: 9
a = + 14 or - 26
  [Simplify.]
Step: 10
Width = a = 14 centimeters
  [Dimensions cannot be negative.]
Step: 11
Length = (a + 12) = (14 + 12) = 26 centimeters
  [Substitute 14 for a and add.]
Step: 12
The book is 14 centimeters wide and 26 centimeters long.
Correct Answer is :   14 cm, 26 cm
Q5A rectangular carpet measures a feet long and (a - 10) feet wide. What are the dimensions of the carpet, if its area is 56 square feet?
A. 15 feet by 5 feet
B. 13 feet by 3 feet
C. 14 feet by 4 feet
D. 16 feet by 6 feet

Solutions
Share 
Step: 1
The area of a rectangle = Length × Width
Step: 2
The area of the rectangular carpet = (a) × (a - 10) square feet
Step: 3
56 = (a) × (a - 10)
  [Original equation.]
Step: 4
56 = a2 - 10a
  [Use distributive property.]
Step: 5
56 + (- 5)2 = a2 - 10a + (- 5)2
  [Add (- 102)2 = (- 5)2 = 25 to each side.]
Step: 6
81 = (a - 5)2
  [Write the right side of the equation as a perfect square and simplify.]
Step: 7
± 9 = (a - 5)
  [Evaluate square roots on both sides.]
Step: 8
± 9 + 5 = a - 5 + 5
  [Add 5 on each side.]
Step: 9
a = - 4 or 14
  [Simplify.]
Step: 10
Length of the rectangular carpet is a = 14 feet.
  [Dimensions cannot be negative.]
Step: 11
Width of the rectangular carpet is (a - 10) = (14 - 10) = 4 feet.
  [Repalce a with 14 and add.]
Step: 12
The dimensions of the carpet are 14 feet by 4 feet.
Correct Answer is :   14 feet by 4 feet
Q6Solve by graphing the related function of the equation 5x2 + 7 = 52.
A. 3
B. + 9 and - 9
C. - 3 and 3
D. 7

Solutions
Share 
Step: 1
ax2 + bx + c = 0
  [The equation in standard form.]
Step: 2
5x2 + 7 = 52
  [Original equation.]
Step: 3
5x2 = 45
  [Subtract 7 from each side.]
Step: 4
x2 = 9
  [Divide with 5 on both sides.]
Step: 5
x2 - 9 = 0
  [Subtract 9 from each side.]
Step: 6
Sketch the graph of the related quadratic function y = x2 - 9
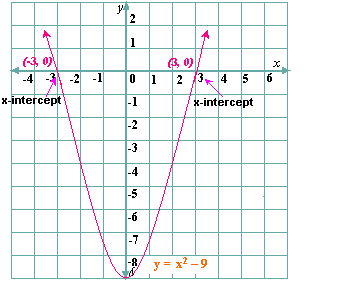
Step: 7
Estimate the values of the x-intercepts. From the graph, the x-intercepts appear to be - 3 and 3.
Step: 8
By substituting x = - 3 and x = 3 in x2 - 9 = 0, it can be observed that - 3 and 3 are solutions of the equation.
Correct Answer is :   - 3 and 3
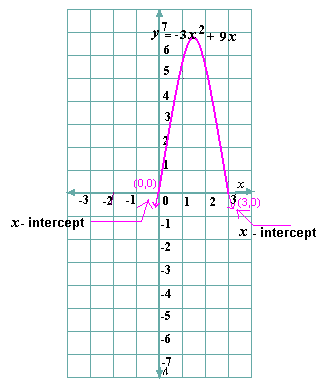
Q7The graph of y = - 3x2 + 9x is shown in the figure. Estimate the solution of - 3x2 + 9x = 0 using the graph.


A. 0 and 1
B. 1 and 2
C. 0 and 2
D. 0 and 3

Solutions
Share 
Step: 1
The x-intercepts in the graph of the equation y = ax2 + bx + c are the solutions of the related equation ax2 + bx + c = 0.
Step: 2
The graph intersects the x-axis at (0, 0) and (3, 0).
Step: 3
So, 0 and 3 are the solutions of the equation.
Correct Answer is :   0 and 3
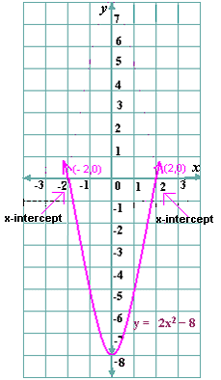
Q8Find the solution of 2x2 - 8 = 0 using the graph.

A. 4 and - 4
B. 2 and - 2
C. 5 and - 5
D. 3 and - 3

Solutions
Share 
Step: 1
2x2 - 8 = 0 is written in the standard form as y = 2x2 - 8.
Step: 2
The graph intersect the x-axis at points (- 2, 0) and (2, 0).
Step: 3
From the graph, the x-intercepts are - 2 and 2.
  [Estimate the values of the x-intercepts.]
Step: 4
2(- 2) 2 - 8 =0
  [Substitute x = - 2 in the equation 2x2 - 8 = 0.]
Step: 5
0 = 0
  [Simplify.]
Step: 6
2(2) 2 - 8 =0
  [Substitute x = 2 in the equation 2x2 - 8 =0.]
Step: 7
0 = 0
  [Simplify.]
Step: 8
Both the values satisfy the equation.
Step: 9
So, 2 and - 2 are the solutions of the equation.
Correct Answer is :   2 and - 2
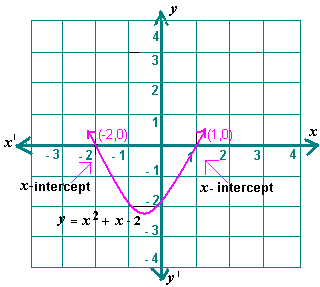
Q9Use the graph to estimate the roots of the equation x2 + x = 2.


A. - 1 and 1
B. - 3 and 1
C. - 4 and 1
D. - 2 and 1

Solutions
Share 
Step: 1
ax2 + bx + c = 0
  [The equation in standard form.]
Step: 2
x2 + x = 2
  [Original equation.]
Step: 3
x2 + x - 2 = 0
  [Subtract 2 from each side.]
Step: 4
Sketch the graph of the related quadratic equation y = x 2 + x - 2.
Step: 5
From the graph, x-intercepts are - 2 and 1.
Step: 6
(- 2) 2 + (- 2) - 2 = 0
  [Substitute x = - 2 in the equation.]
Step: 7
0 = 0
  [Simplify.]
Step: 8
(1)2 + 1 - 2 = 0
  [Substitute x = 1 in the equation.]
Step: 9
0 = 0
  [Simplify.]
Step: 10
The values x = - 2 and 1 satisfy the equation x2 + x - 2 = 0.
Step: 11
So, - 2 and 1 are the roots of the equation.
Correct Answer is :   - 2 and 1
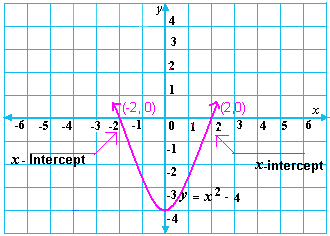
Q10Estimate the solution of the equation 5x2 = 20 using a graph.


A. - 5 and 5
B. - 4 and 4
C. - 2 and 2
D. - 3 and 3

Solutions
Share 
Step: 1
ax2 + bx + c = 0
  [The equation in standard form.]
Step: 2
5x2 = 20
  [Original equation.]
Step: 3
5x2 - 20 = 0
  [Subtract 20 from each side.]
Step: 4
x2 - 4 = 0
  [Divide by 5 on each side.]
Step: 5
Sketch the graph of the related quadratic function, y = x2 - 4.
Step: 6
From the graph, x-intercepts are - 2 and + 2.
Step: 7
(- 2) 2 - 4 = 0
  [Substitute x = - 2 in the equation.]
Step: 8
0 = 0
  [Simplify.]
Step: 9
(2) 2 - 4 = 0
  [Substitute x = 2 in the equation.]
Step: 10
0 = 0
  [Simplify.]
Step: 11
Both the values x = - 2 and x = 2 satisfy the equation x2 - 4 = 0.
Step: 12
So, the solutions of the equation are - 2 and 2.
Correct Answer is :   - 2 and 2
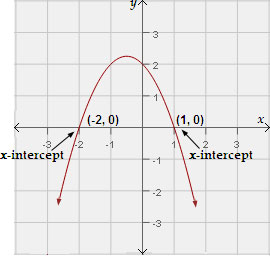
Q11Solve the quadratic equation - 4x2 - 4x + 8 = 0 using the graph.

A. - 3 and 1
B. - 4 and 1
C. - 2 and 1
D. - 2 and - 3

Solutions
Share 
Step: 1
ax2 + bx + c = 0
  [The equation in standard form.]
Step: 2
- 4x2 - 4x + 8 = 0
  [Original equation.]
Step: 3
- x2 - x + 2 = 0
  [Divide each side by 4.]
Step: 4
Sketch the graph of the related quadratic function, y = - x2 - x + 2.
Step: 5
From the graph, x-intercepts are - 2 and 1.
Step: 6
- (- 2) 2 - (- 2) + 2 = 0
  [Substitute x = - 2 in the equation.]
Step: 7
0 = 0
  [Simplify.]
Step: 8
- (1) 2 - (1) + 2 = 0
  [Substitute x = 1 in the equation.]
Step: 9
0 = 0
  [Simplify.]
Step: 10
Both the values x = - 2 and x = 1 satisfy the equation.
Step: 11
So, the solutions of the equation are - 2 and 1.
Correct Answer is :   - 2 and 1
Q12Laura dives into a pool from the diving board, that is 16 feet high from the water. She dives with an initial downward velocity of - 24 feet per second. If the equation to model the height of the dive is h = - 16t2 + (- 24)t + 16, then find the time in seconds it takes Laura to reach the water.
A. 1
B. 1.5
C. 5.50
D. 0.50

Solutions
Share 
Step: 1
h = - 16t2 + (- 24)t + 16
  [Original equation.]
Step: 2
0 = - 16t2 + (- 24t) + 16
  [Replace h with 0, as the height is zero at the water level.]
Step: 3
t = {-(-24)±[(-24)2-4(-16)(16)]}[2(-16)]
  [Substitute a = - 16, b = - 24 and c = 16 in the quadratic formula.]
Step: 4
t = 24±576+1024-32
  [Simplify.]
Step: 5
t = 24±1600-32
  [Simplify inside the radical.]
Step: 6
t = 24±40-32 = -2, 0.50
  [Simplify the radical.]
Step: 7
t = 0.50
  [Since t represents time, consider the positive integer.]
Correct Answer is :   0.50
Q13Jake jumped from a 729 feet bungee tower. Find the time it took him to reach the ground, if the equation that models his height is h = - 16t2 + 729, where t is the time in seconds.

A. 6.50
B. 7
C. 7.25
D. 6.75

Solutions
Share 
Step: 1
h = - 16t2 + 729
  [Original equation.]
Step: 2
0 = - 16t2 + 729
  [Replace h with 0, as the height is zero at the ground level.]
Step: 3
t = {-(-0)±[(-0)2-4(-16)(729)]}[2(-16)]
  [Substitute the values in the quadratic formula: a = - 16, b = 0 and c = 729.]
Step: 4
= 0±(0+46656)-32
  [Simplify.]
Step: 5
= 0±46656-32
  [Simplify inside the radical.]
Step: 6
= 0±216-32
  [Simplify.]
Step: 7
= -216-32 = 6.75
  [Since t represents time, use the positive solution.]
Correct Answer is :   6.75
Q14The base of a triangle is 4 cm longer than the altitude. Find the length of the base if the area of the triangle is 48 cm2.
A. 12 cm
B. 8 cm
C. 14 cm
D. None of the above

Solutions
Share 
Step: 1
Let x be the length of the altitude of the triangle & the length of its base = (x + 4) cm.
Step: 2
The area of a triangle = 12 × base × altitude
Step: 3
48 = 12 × (x + 4) × x
  [Substitute the values.]
Step: 4
48 = 12 × (x2 + 4x)
  [Distributive property.]
Step: 5
96 = (x2 + 4x)
  [Multiply throughout by 2.]
Step: 6
x2 + 4x - 96 = 0
  [Subtract 96 from the two sides of the equation.]
Step: 7
(x + 12)(x - 8) = 0
  [Factor.]
Step: 8
Therefore, x = - 12 or 8.
Step: 9
Reject the negative solution, as the length cannot be negative.
So, x = 8 and x + 4 = 8 + 4 = 12
Step: 10
So, the length of the base of the triangle is 12 cm.
Correct Answer is :   12 cm
Q15Solve by graphing the related function of the equation x2 + x = 2.

A. - 3 and 7
B. - 2 and 1
C. - 3 and 6
D. 2 and 1

Solutions
Share 
Step: 1
x2 + x = 2
  [Original equation.]
Step: 2
x2 + x - 2 = 0
  [Subtract 2 from each side.]
Step: 3
Sketch the graph of the related quadratic function y = x2 + x - 2 as shown below.
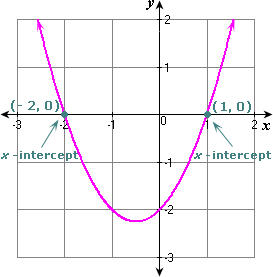
Step: 4
From the graph, the x-intercepts appear to be - 2 and 1.
  [Estimate the values of the x-intercepts.]
Step: 5
So, - 2 and 1 are the solutions of the equation.
Correct Answer is :   - 2 and 1

HighSchool Math