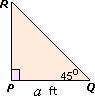Solved Examples and Worksheet for Trigonometric Ratios

Q1Find the value of tan R, if a = 24 units, b = 32 units and c = 40 units.

A. 53
B. 35
C. 34
D. 43

Solutions
Share 
Step: 1
tan R = Opposite side of RAdjacent side of R
Step: 2
PQ = 24 units
RP = 32 units
  [PQ¯ is the opposite side of R and RP¯ is the adjacent side of R.]
Step: 3
In ΔPQR, tan R = PQRP
Step: 4
tan R = 2432 = 34
  [Substitute the values of PQ and RP.]
Correct Answer is :   34
Q2What is the length of side RP¯ in ΔPQR? [a = 16.]

A. 18 ft
B. 16 ft
C. 17 ft
D. 20 ft

Solutions
Share 
Q3What is the ratio of AC to BC in the figure, if tan A = 23?


A. 3 : 4
B. 4 : 3
C. 3 : 2
D. 2 : 3

Solutions
Share 
Step: 1
Tan is the ratio between opposite side and adjacent side.
Step: 2
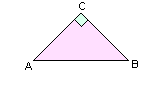
In the figure, tan A = BCAC
Step: 3
tan A = 23
Step: 4
BCAC = 23
  [From steps 2 and 3.]
Step: 5
The ratio of AC to BC is 3 : 2.
Correct Answer is :   3 : 2
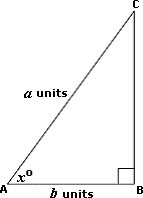
Q4Find tan x in right triangle ABC for a = 25 and b = 7.

A. 247
B. 2425
C. 725
D. 257

Solutions
Share 
Step: 1
BC = AC2-AB2
  [Use the Pythagorean theorem.]
Step: 2
BC = 252-72 = 24 units
  [Substitute and simplify.]
Step: 3
tan x° = BCAB
  [Use the tangent ratio.]
Step: 4
tan x° = 247
  [Substitute.]
Correct Answer is :    247
Q5In ΔABC, cos A = 817. Find the value of sin A.


A. 815
B. 158
C. 817
D. 1517

Solutions
Share 
Step: 1
In ΔABC, cos A = adjacent side to Ahypotenuse
Step: 2
= ABAC = 817
  
Step: 3
In ΔABC, BC = AC2-AB2
  [Apply the Pythagorean theorem.]
Step: 4
BC = 172-82 = 15 cm
  [Substitute and simplify.]
Step: 5
In ΔABC, sin A = opposite side to Ahypotenuse
Step: 6
= BCAC = 1517
  [Substitute.]
Correct Answer is :   1517
Q6Find the value of tan R, if a = 12 units, b = 16 units and c = 20 units.

A. 35
B. 34
C. 43
D. 53

Solutions
Share 
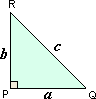
Step: 1
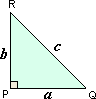
tan R = Opposite side of ∠RAdjacent side of ∠R.
Step: 2
PQ = 12 units
RP = 16 units
  [PQ¯ is the opposite side of R and RP¯ is the adjacent side of ∠R.]
Step: 3
In ΔABC, tan R = PQRP
Step: 4
tan R = 1216 = 34
  [Substitute the values of PQ and RP.]
Correct Answer is :   34
Q7Find the value of sin A, if x = 7 units, y = 24 units, and z = 25 units.

A. 725
B. 2524
C. 2425
D. 257

Solutions
Share 
Step: 1
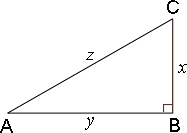
sin A = Side opposite to AHypotenuse
Step: 2
In the triangle, BC¯ is the side opposite to A and AC¯ is the hypotenuse.
Step: 3
sin A = BCAC
  
Step: 4
= 725
  [Substitute BC = 7 and AC = 25.]
Correct Answer is :   725
Q8Find the values of sin θ and cos θ from the given figure. [a = 32, b = 24 and c = 40]

A. 34 , 45
B. 35 , 45
C. 34 , 43
D. 45 , 35

Solutions
Share 
Step: 1
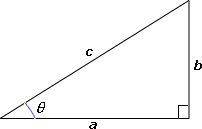
sin θ = opposite sidehypotenuse , cos θ = adjacent sidehypotenuse
  [Definition.]
Step: 2
sin θ = 2440 = 35
  [Substitute the values from the given figure.]
Step: 3
cos θ = 3240 = 45
  [Substitute the values from the given figure.]
Correct Answer is :   35 , 45
Q9The value of tan R,for a = 21 units, b = 28 units and c = 35 units is ___________.


A. 35
B. 43
C. 34
D. 53

Solutions
Share 
Step: 1
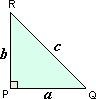
tan R = Opposite side of RAdjacent side of R.
Step: 2
PQ = 27 units
RP = 36 units
  [PQ¯ is the opposite side of R and RP¯ is the adjacent side of R.]
Step: 3
In ΔPQR, tan R = PQRP
Step: 4
tan R = 2736 = 34
  [Substitute the values of PQ and RP.]
Correct Answer is :   34

HighSchool Math