Solved Examples and Worksheet for Congruent Triangles

Q1ΔABD and ΔCDB are congruent in the figure. Which of the following statements is always true?

A. ∠x is congruent to ∠z.
B. ∠z is congruent to ∠y.
C. ∠x is congruent to ∠y.
D. None of the above

Solutions
Share 
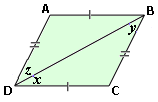
Step: 1
ΔABD and ΔCDB are congruent.
Step: 2
In congruent triangles, the angles opposite to equal sides are equal.
Step: 3
∠y is always equal to ∠z.
  [Alternate interior angles.]
Step: 4
∠z ≅ ∠y is always true.
Correct Answer is :   ∠z is congruent to ∠y.
Q2In triangles SPT and ONM, ∠S ≅ ∠M, ∠P ≅ ∠O and PT¯ ≅ ON¯; ΔSPT is congruent to
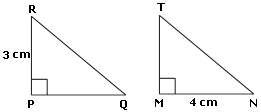
A. ΔMNO
B. ΔMON
C. ΔOMN
D. ΔONM

Solutions
Share 
Step: 1
In triangles SPT and ONM, ∠S ≅ ∠M, ∠P ≅ ∠O and PT¯ ≅ ON¯
  [Given.]
Step: 2

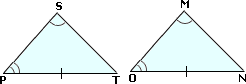
Step: 3
If two angles and a nonincluded side of one triangle are congruent to two angles and the corresponding nonincluded side of another triangle, then the triangles are congruent.
  [AAS theorem.]
Step: 4
ΔSPT ≅ ΔMON
  [From step 3.]
Correct Answer is :   ΔMON
Q3ΔPQR ≅ ΔMNT. What is the length of TN?

A. 4 cm
B. 3 cm
C. 5 cm
D. 6 cm

Solutions
Share 
Step: 1
TM = RP
  [ΔPQR ≅ ΔMNT.]
Step: 2
TM = 3 cm
  [Step 1.]
Step: 3
TN = TM2+MN2
  [Pythagorean Theorem.]
Step: 4
TN = 32+42
  [Substitute.]
Step: 5
TN = 5 cm.
  [Simplify.]
Correct Answer is :   5 cm
Q4Which of the following is true?


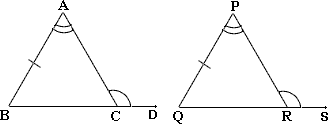
A. ΔABC ≅ ΔPQR
B. ΔABC ≅ ΔPRQ
C. ΔABC ≅ ΔRPQ
D. ΔABC ≅ ΔQRP

Solutions
Share 
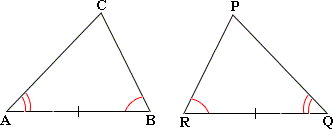
Step: 1
From the figure ∠ABC ≅ ∠QRP, ∠CAB ≅∠PQR, and BA¯ ≅ RQ¯
Step: 2
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
  [ASA Postulate.]
Step: 3
So, ΔABC ≅ ΔQRP
Correct Answer is :   ΔABC ≅ ΔQRP
Q5AB¯ is parallel to CD¯, AE¯ is parallel to BD¯. BC¯ is parallel to DE¯ as shown. Which of the following is correct?


A. ΔABC ≅ ΔECD
B. ΔACB ≅ ΔCDE
C. ΔABC ≅ ΔCDE
D. ΔABC ≅ ΔCED

Solutions
Share 
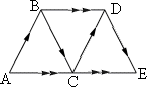
Step: 1
ACDB, CEDB are parallelograms in which AB¯ ≅ CD¯, AC¯ ≅ BD¯ ≅ CE¯ and BC¯ ≅ DE¯.
  [From the figure.]
Step: 2
If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.
  [SSS postulate.]
Step: 3
So, ΔABC and ΔCDE are congruent to each other.
Correct Answer is :   ΔABC ≅ ΔCDE
Q6Are the triangles congruent?

A. cannot be determined
B. no
C. yes

Solutions
Share 
Step: 1
From the figure,
AB¯ ≅ PQ¯
∠ACD ≅ ∠PRS
∠BAC ≅ ∠QPR
Step: 2
If the two angles and the non included side of one triangle are congruent to the two angles and the non included side of another triangle, then the two triangles are congruent.
  [By AAS postulate.]
Step: 3
As the corresponding parts of the triangles are congruent, the triangles are congruent.
Correct Answer is :   yes
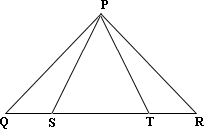
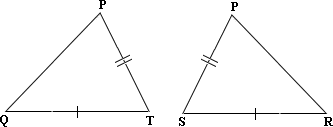
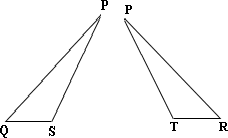
Q7If PS¯ ≅ PT¯, QT¯ ≅ RS¯, which of the following are true?
1. ΔPSR ≅ ΔPTQ
2. ΔPQS ≅ ΔPRT
3. PQ¯ ≅ PR¯
4. QS¯ ≅ TR¯

A. 1,2
B. 3,4
C. 1,2,4
D. all are correct

Solutions
Share 
Step: 1
Given, QT¯ ≅ RS¯.
Step: 2
⇒ QS + ST = ST + TR ⇒QS¯ ≅ TR¯ which is true.
Step: 3
Consider ΔPSR and ΔPTQ. In ΔPSR, SR = ST + TR and in ΔPTQ, QT = QS + ST ⇒ QT = TR + ST = SR
  [Substitute QS = TR.]
Step: 4
⇒ SR¯ ≅ QT¯
Step: 5
So, ΔPSR ≅ ΔPTQ which is true.
  [SSS postulate.]

Step: 6
Consider ΔPQS, ΔPRT, QS¯ ≅ RT¯ and PS¯ ≅ PT¯
Step: 7
So, ΔPQS ≅ ΔPRT which is true.
  [SSS postulate.]

Step: 8
PQ¯ ≅ PR¯ which is true.
  [ΔPQS ≅ ΔPRT.]
Correct Answer is :   all are correct
Q8Which of the following conditions is always true for congruent triangles?
A. A pair of triangles have two proportional angles.
B. A pair of triangles have equal sides.
C. A pair of triangles have an equal angle and two equal sides.
D. A pair of triangles have equal hypotenuses as well as an equal angle.

Solutions
Share 
Step: 1
Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in size.
Correct Answer is :   A pair of triangles have equal sides.
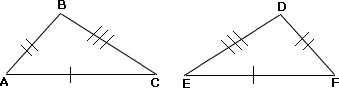
Q9In the triangles shown, AB¯ ≅ FD¯, AC¯ ≅ EF¯ and BC¯ ≅ DE¯. Identify a congruence statement for the two triangles.

A. ΔCAB ≅ ΔEDF
B. ΔABC ≅ ΔDEF
C. ΔABC ≅ ΔFDE
D. ΔACB ≅ ΔEFD

Solutions
Share 
Step: 1
AB¯ ≅ FD¯, AC¯ ≅ EF¯ and BC¯ ≅ DE¯
  [Given.]
Step: 2
Therefore, by SSS property, ΔABC ≅ ΔFDE.
Correct Answer is :   ΔABC ≅ ΔFDE
Q10What is the measure of ∠A, if ΔABC is congruent to ΔDEF ?


A. 45°
B. 55°
C. 50°
D. 30°

Solutions
Share 
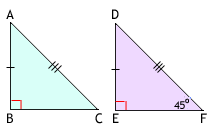
Step: 1
In ΔDEF, m∠E = 90° and m∠F = 45°.
Step: 2
Sum of the angles of a triangle is equal to 180°.
Step: 3
m∠D + m∠E + m∠F = 180°
Step: 4
m∠D + 90° + 45° = 180°
  [Substitute the measures of angles E and F.]
Step: 5
m∠D + 135° = 180°
  [Simplify.]
Step: 6
m∠D = 45°
  [Subtraction property for equality.]
Step: 7
ΔABC is congruent to ΔDEF.
Step: 8
So, the corresponding angles and sides of ΔABC and ΔDEF are equal.
Step: 9
AB = DE, so, m∠F = m∠C
  [In congruent triangles, the angles opposite to the equal sides are equal. ]
Step: 10
m∠B = m∠E so, m∠A = m∠D.
Step: 11
m∠A = m∠D = 45°
Step: 12
So, the measure of ∠A is 45°.
Correct Answer is :   45°

HighSchool Math