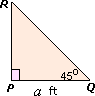Special Right Triangles-Geometry-Solved Examples

Solved Examples and Worksheet for Special Right Triangles

Q1If the length of the leg opposite to the 60° angle in a 30° - 60° - 90° triangle is 93 cm, then the length of the hypotenuse is
A. 33 cm.
B. 9 cm.
C. 6 cm.
D. 18 cm.

Solutions

Step: 1

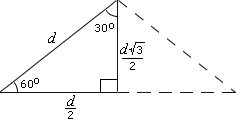
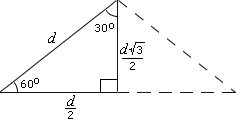
If d is the length of the hypotenuse in a 30°- 60° - 90° triangle, then the length of the side opposite the 60° angle is d32 .

Step: 2

So, d32 = 93

Step: 3

d = 93⋅23 = 18 cm

Correct Answer is : 18 cm.

Q2If the length of the leg of a 45° - 45° - 90° triangle is 15 ft, then the length of the hypotenuse is
A. 92ft
B. 9 ft
C. 152 ft.
D. 3 ft

Solutions

Step: 1

If S is the length of the leg of a 45° - 45° - 90° triangle, then the length of the hypotenuse is S2 = 152 ft.

Correct Answer is : 152 ft.

Q3If the length of the hypotenuse of a 45°- 45° - 90° triangle is 10 cm then the length of each leg is

A. 8 cm.
B. 52 cm.
C. 43 cm.
D. 83 cm.

Solutions

Step: 1

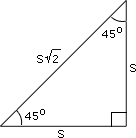
If S is the length of the leg of a 45° - 45° - 90° triangle, then the length of the hypotenuse is S2.

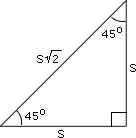
Step: 2

So, S2 = 10

Step: 3

S = 102

Step: 4

S = 1022 ×2 = 1022 = 52 cm

Correct Answer is : 52 cm.

Q4What is the relation between the length of the shortest side and hypotenuse in a 30^o-60^o-90^o triangle?

A. shortest side is √32^th of the hypotenuse
B. shortest side is half of the hypotenuse
C. shortest side is 34^th of the hypotenuse
D. shortest side is 14^th of the hypotenuse

Solutions

Step: 1

In a 30^o - 60^o - 90^o triangle, the length of the shortest side is half of its hypotenuse.

Correct Answer is : shortest side is half of the hypotenuse

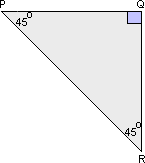
Q5The length of PR in the figure is 72 inches. What are the lengths of PQ¯ and QR¯?

A. 8 inches and 9 inches
B. 7 inches and 7 inches
C. 8 inches and 7 inches
D. 7 inches and 9 inches

Solutions

Step: 1

The triangle is a 45^o - 45^o - 90^o triangle.

Step: 2

Length of PR = 72 inches.

Step: 3

In a 45^o - 45^o - 90^o triangle, length of hypotenuse is 2 times the length of leg.

Step: 4

In ΔPQR, PQ¯ and QR¯ are congruent legs and PR¯ is the hypotenuse.

Step: 5

PR = PQ2

Step: 6

PQ = PR2

[Divide each side by 2.]

Step: 7

PQ = 722

[Replace PR with 72.]

Step: 8

PQ = 7 inches

[Simplify.]

Step: 9

Since the lengths of two legs are equal in 45^o - 45^o - 90^o triangle, PQ = QR = 7 inches.

Step: 10

The lengths of PQ¯ and QR¯ are 7 inches.

Correct Answer is : 7 inches and 7 inches

Q6The lengths of two legs are equal and hypotenuse is 2 times the length of a leg in a triangle. Which of the following are the angles of the triangle?

A. 60^o - 60^o - 60^o
B. 30^o - 60^o - 90^o
C. 45^o - 45^o - 90^o
D. 90^o - 90^o - 90^o

Solutions

Step: 1

In a 45^o - 45^o - 90^o triangle, the lengths of two legs are same and length of hypotenuse is 2 times the length of a leg.

Step: 2

The triangle is a 45^o - 45^o - 90^o triangle.

Correct Answer is : 45^o - 45^o - 90^o

Q7Is a triangle with side lengths 3, 6 and 33 a 30^o-60^o-90^o triangle?

A. no, it is not a right triangle
B. yes
C. no, it is an equilateral triangle
D. no, it is a 45^o- 45^o- 90^o triangle

Solutions

Step: 1

The side lengths of the triangle are 3, 6 and 33.

Step: 2

6² = 3² + (33) ²

[Checking for Pythagorean theorem.]

Step: 3

Since given measures satisfy Pythagorean theorem, they form a right triangle.

Step: 4

Here, the length of hypotenuse is 6 and the length of shorter leg is 3.

Step: 5

Since the length of hypotenuse is twice the length of shorter leg, the sides form a 30^o - 60^o - 90^o triangle.

Correct Answer is : yes

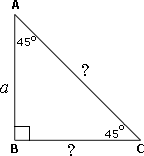
Q8Find the missing sides in the triangle. [a = 5 cm.]

A. BC = 10 cm and AC = 252 cm
B. BC = 52 cm and AC = 5 cm
C. BC = 5 cm and AC = 52 cm
D. BC = 4 cm and AC = 7 cm

Solutions

Step: 1

Since two of the angles of the triangle are equal and one of the angle is 90^o, the triangle is an isosceles right triangle.

Step: 2

In an isosceles right triangle,the legs have same length and hypotenuse is 2 times its leg.

Step: 3

AB¯, BC¯ are legs and AC¯ is the hypotenuse from the figure.

Step: 4

BC = AB = 5 cm

[Since legs have same lengths in an isosceles right triangle.]

Step: 5

AC = BC × 2 cm = 52 cm

[Substitute BC = 5.]

Step: 6

The missing sides are BC = 5 cm and AC = 52 cm.

Correct Answer is : BC = 5 cm and AC = 52 cm

Q9What is the length of side RP¯ in ΔPQR? [a = 16.]

A. 18 ft
B. 16 ft
C. 17 ft
D. 20 ft

Solutions

Q10The area of a 30^o - 60^o- 90^o triangle is 73 units². Find the length of the shorter leg.

A. 3 units
B. 3.74 units
C. 7.48 units
D. 3.74 3 units

Solutions

Step: 1

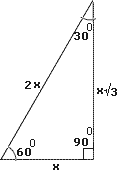
Let x units be the length of the shorter side.

Step: 2

[30^o-60^o-90^o-triangle theorem.]

Step: 3

Area of the triangle = (12) × base × height

[Formula.]

Step: 4

73 = 12 × x × x3

[Substitute.]

Step: 5

x² = 14

[Simplify.]

Step: 6

x = 3.74

[Take square root on both sides.]

Step: 7

Length of the shorter leg is 3.74 units.

Correct Answer is : 3.74 units

Q11The area of 45^o- 45^o - 90^o triangle is 8 in.². What is the length of the hypotenuse?

A. 43 in.
B. 4 in.
C. 8 in.
D. 42 in.

Solutions

Step: 1

Let x can be the length of the leg

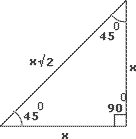
Step: 2

[45^o-45^o-90^o Triangle Theorem.]

Step: 3

Area of the triangle = 12 × base × height

[Formula.]

Step: 4

8 = 12 × x × x

[Substitute.]

Step: 5

x² = 16

[Simplify.]

Step: 6

x = 4

[Take square roots on Both sides.]

Step: 7

Hypotenuse = x2 = 42 in.

[Step2 and step6.]

Correct Answer is : 42 in.

Q12The hypotenuse of a 30^o - 60^o - 90^o triangle is 43 cm more than the shorter leg. What is the length of the longer leg?
A. 43 cm
B. 4 cm
C. 8 3 cm
D. 12 cm

Solutions

Step: 1

Let x be the length of the shorter leg.

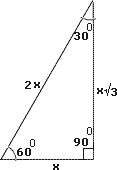
Step: 2

[30^o-60^o-90^o-triangle theorem.]

Step: 3

Hypotenuse = shorter leg + 43

[Given.]

Step: 4

2x = x + 43

[Substitute.]

Step: 5

x = 43

[Simplify.]

Step: 6

Length of the longer leg = x3 = 3 × 43 = 12 cm

[Step2 and step5.]

Correct Answer is : 12 cm

Solved Examples and Worksheet for Special Right Triangles

Related Worksheet

Related Topic

HighSchool Math