Application Problems involving Trigonometric Functions-Geometry-Solved Examples

Solved Examples and Worksheet for Application Problems involving Trigonometric Functions

Q1A pillar of height 227 ft casts a shadow of 363 ft long. Find the approximate measure of the angle of elevation of the sun.

A. 44°
B. 55°
C. 46°
D. 32°

Solutions

Step: 1

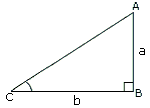
Length of the pillar, a = 227 ft.

Step: 2

Length of the shadow, b = 363 ft.

Step: 3

Step: 4

∠ACB is the angle of elevation of the sun.

Step: 5

In right triangle ABC, tan C = 227363

[Use tan C = ABBC = ab.]

Step: 6

tan C ≈ 0.625344

[Simplify.]

Step: 7

∠C ≈ 32°

[Use calculator to find the measure of ∠C.]

Step: 8

So, angle of elevation of the sun is 32°

Correct Answer is : 32°

Q2A boy stands at 198 m away from the base of a tower of height 267 m. Find the angle of depression of the boy from the top of the tower.
A. 47° 52′
B. 53° 26′
C. 43° 38′
D. 37° 34′

Solutions

Step: 1

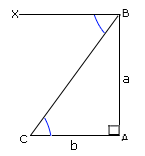
Let AB be the height of the tower and C be the position of boy in the figure.
AB = 282 m and AC = 168 m.

Step: 2

Step: 3

∠XBC = ∠BCA

[AC¯ and BX¯ are parallel, the angles of elevation and depression are equal in measure.]

Step: 4

In right triangle CAB, tan C = 282168 ≈ 1.6969

[Use tan C = ABAC.]

Step: 5

∠C ≈ 59° 13′

[Use calculator to find the measure of ∠C.]

Step: 6

Angle of depression of the boy from the top of the tower is 59° 13′.

Correct Answer is : 53° 26′

Q3A flagpole is placed on top of the building. From a point on the ground d = 270 ft from the base of a building, the angles of elevation of the top and bottom of the flagpole are 70°15′ and 57°20′. Find the height of the flagpole.
A. 752 ft
B. 1173 ft
C. 421 ft
D. 331 ft

Solutions

Step: 1

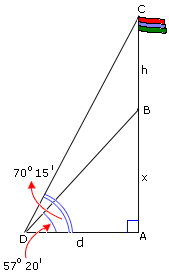
Let the height of the flagpole, BC = h and the height of the building, AB = x

Step: 2

D is the point of observation.

Step: 3

tan 57°20′ = x230

[tan ∠BDA = ABAD.]

Step: 4

x = 230 Tan 57°20′ ≈ 230 (1.559655234) ≈ 359 ft.

Step: 5

tan 70°15′ = x + h230

[tan ∠CDA = ACAD.]

Step: 6

x + h = 230 tan 70°15′

Step: 7

x + h ≈ 230 × (2.785230695) ≈ 641

Step: 8

359 + h = 641

Step: 9

h = 641 - 359 = 282

Step: 10

So, the height of flagpole is 282 ft.

Correct Answer is : 331 ft

Q4Two boys are standing on either side of a pole that is h = 130 m long. Their angles of elevation of the top of the pole measures 30°20′ and 45°30′. Find the distance between the two boys. (The position of the boys and the foot of the pole are collinear.)
A. 222 m
B. 128 m
C. 350 m
D. 94 m

Solutions

Step: 1

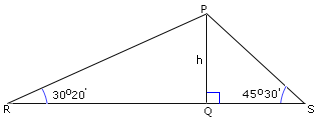
Height of the pole, PQ = 120 m and R & S be the position of boys on either side of the pole.

Step: 2

tan 30°20′ = 120QR

[tan R = PQQR.]

Step: 3

QR = 120tan30o20'

Step: 4

QR ≈ 205 m

Step: 5

tan 45o30' = 120QS

[tan S = PQQS.]

Step: 6

QS = 120tan45o30' ≈ 118 m

Step: 7

RS = QR + QS = 205 + 118 = 323 m

Step: 8

So, the distance between the boys is 323 m.

Correct Answer is : 350 m

Q5From a point d = 25 ft away from the foot of a tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
A. 13 ft
B. 14 ft
C. 22 ft
D. 43 ft

Solutions

Step: 1

Let x represent the height of the tower.

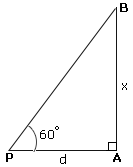
Step: 2

In right triangle PAB,

Step: 3

tan 60° = x25.

Step: 4

x = 25 tan 60°.

Step: 5

x ≈ 43 ft.

Step: 6

The height of the tower is 43 ft.

Correct Answer is : 43 ft

Q6The angle of elevation of the top of a tower from a point on the ground is 60°. If the height of the tower is 119 m, then find the distance of the point from the foot of the tower.
A. 1193 m
B. 3119 m
C. 1193 m
D. 119 m

Solutions

Step: 1

Draw the figure from the given data.

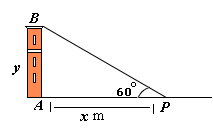
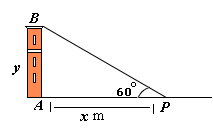
Step: 2

P is the point on the ground.

Step: 3

Let x be the distance of point P from the foot of the tower.

Step: 4

Height of the tower AB = y = 130 m

[Given.]

Step: 5

In right triangle PAB, tan 60° = 130x.

Step: 6

x = 130tan 60°

Step: 7

x = 1303

[Substitute the value of tan 60°.]

Step: 8

So, the distance of the point P from the foot of the tower = 1303 m.

Correct Answer is : 1193 m

Q7The angle of elevation of the top of a tree is 20^o from a point 25 ft away from the foot of the tree. Find the height of the tree rounded to the nearest feet.

A. 26 ft
B. 30 ft
C. 21 ft
D. 9 ft

Solutions

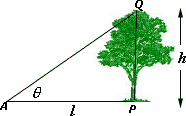
Step: 1

The measure of the angle of elevation from point A is 35°.

Step: 2

In right triangle APQ, tan 35° = h25

[l = 22 ft.]

Step: 3

⇒ h = 25 × 0.7

[Substitute the value of tan 35°.]
[Use calculator.]

Step: 4

⇒ h ≈ 18 ft

[Simplify.]

Step: 5

So, the height of the tree is 18 ft.

Correct Answer is : 9 ft

Q8A flagstaff stands on the top of a building. At a distance of 26 ft away from the foot of the building, the angle of elevation of the top of a flagstaff is 46° and the angle of elevation of the top of a building is 30°. Find the height of the flagstaff to the nearest feet.

A. 9 ft
B. 9 ft
C. 18 ft
D. 12 ft

Solutions

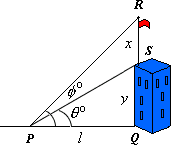
Step: 1

Draw a figure for the given data.

Step: 2

Q is the foot of the building. Let x represent the height of the flagstaff and y represent the height of the building.

Step: 3

In right triangle PQS, tan 40° = y24

Step: 4

y = 24 tan 40° = 24 × 0.83 ≈ 19.92

[Substitute the value of tan 40° .]

Step: 5

In right triangle PQR, tan 55° = x + y24

Step: 6

x + y = 24 tan 55°

Step: 7

x + y = 24 × 1.42

[Substitute the value of tan 55° .]

Step: 8

x + 19.92 = 34.08

[Substitute the value of y.]

Step: 9

x ≈ 14

Step: 10

Height of the flagstaff is 14 ft.

Correct Answer is : 12 ft

Q9From the top of a building of height h meters in a street, the angles of elevation and depression of the top and the foot of another building on the opposite side of the street are θ° and φ° respectively. Find the height of the opposite building. [Given h = 90, φ = 40, and θ = 55.]

A. 265 meters
B. 255 meters
C. 270 meters
D. 260 meters

Solutions

Step: 1

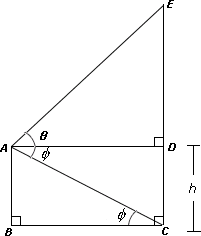
Draw the figure from the given data.

Step: 2

Let AB represent the first building and CE represent the opposite building.

Step: 3

CD = AB = 50 meters

[The opposite sides of a rectangle.]

Step: 4

In right triangle ABC, tan 25° = ABBC

Step: 5

⇒ 0.466 = 50BC

[Substitute the value of tan 25° and simplify.]

Step: 6

⇒ BC ≈ 107.296 meters

Step: 7

AD = BC ⇒ AD = 107 meters

[Opposite sides of a rectangle.]

Step: 8

In right triangle ADE, tan 40° = DEAD

Step: 9

⇒ 0.839 = DE107

[From step 7.]

Step: 10

⇒ DE ≈ 89.77 meter

[Substitute the value of tan 40° and simplify.]

Step: 11

Therefore, the height of the opposite building CE = CD + DE

Step: 12

⇒ 107.296 + 89.77

Step: 13

⇒ ≈ 197 meters.

Step: 14

Therefore, the height of the opposite building is 197 meters.

Correct Answer is : 260 meters

Q10Two towers are constructed on a plot of land. The angle of depression of the top of the second tower when seen from the top of the first tower is 30°. If the height of the first tower is 130 ft and the height of the second tower is 68 ft, then find the horizontal distance between the two towers.

A. 119 ft
B. 109 ft
C. 119 ft
D. 114 ft

Solutions

Step: 1

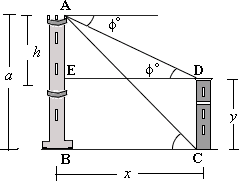
Draw the figure for the given data.

Step: 2

Height of the first tower, AB = 130 ft

Step: 3

Height of the second tower, CD = 86 ft

Step: 4

Let the distance between the two towers, BC = ED = x ft.

Step: 5

Let the difference between the heights of the two towers, AE = h ft.

Step: 6

In right triangle AED, tan 20° = AEED = hx
⇒ h = 0.36x

[Substitute the value of tan 20° and simplify.]

Step: 7

From the figure, AE = AB - BE
⇒ AE = 130 - 86 = 44 ft.

[From the figure AE = h.]

Step: 8

44 = 0.36x

[From step 6 and step 7.]

Step: 9

⇒ x ≈ 122 ft.

Step: 10

So, the distance between the two towers is 122 ft.

Correct Answer is : 109 ft

Q11The angle of elevation of the top of a tower measures 52° from a point on the ground 22 ft from the base of it. Fnd the height of the tower.

A. 28 ft
B. 30 ft
C. 22 ft
D. 17 ft

Solutions

Step: 1

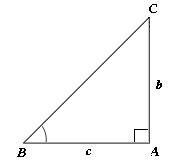
Let b be the height of the tower.

Step: 2

tan 52° = b22

Step: 3

b = 22 tan 52°

Step: 4

b = 22 × (1.27994) = 28

Step: 5

So, the height of the tower is 28 ft.

Correct Answer is : 28 ft

Q12A building is of height 140 m.Two boys on either side of the tower observed the angles of elevation of the top of the tower as 30°18′ and 40°20′. Find the distance between the boys.

A. 175 m
B. 405 m
C. 180 m
D. 310 m

Solutions

Step: 1

Let AD = 140 m, be the height of the building and B & C be the position of boys on either side of the building with ∠B = 30°18′ and ∠C = 40°20′ .

Step: 2

tan 30°18′ = 140DB

[tan B = ADDB.]

Step: 3

DB = 140tan30o18'

Step: 4

DB = 240 m

Step: 5

tan 40o20' = 140DC

[tan C = ADDC.]

Step: 6

DC = 140tan40o20' = 165 m

Step: 7

BC = DB + DC = 240 + 165 = 405 m

Step: 8

So, the distance between the boys is 405 m.

Correct Answer is : 405 m

Q13A girl stands at 120 m from the base of a tree whose height is 180 m. Find the angle of depression of the girl from the top of the tree.

A. 44°28′
B. 56°18′
C. 66°14′
D. 23°18′

Solutions

Step: 1

Let MN = 180 m be the length of the tree.

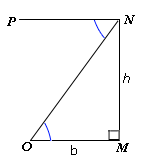
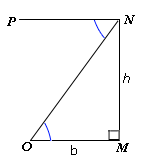
Step: 2

Let MO = 120 m be the distance of the girl from the base of the tree.

Step: 3

∠PNO = ∠NOM

[MO¯ and NP¯ are parallel, the angles of elevation and depression are equal in measure.]

Step: 4

tan O = 180120

[tan O = MNMO.]

Step: 5

∠O = 56°18′

Correct Answer is : 56°18′

Solved Examples and Worksheet for Application Problems involving Trigonometric Functions

Related Worksheet

Related Topic

HighSchool Math