Law of Sines and Cosines to Solve Triangles-Geometry-Solved Examples

Solved Examples and Worksheet for Law of Sines and Cosines to Solve Triangles

Q1In triangle ABC, if a = 4, b = 3, and c = 5, then find the measure of the angle opposite to the longest side to the nearest degree.

A. 0^o
B. 45^o
C. 90^o
D. 60^o

Solutions

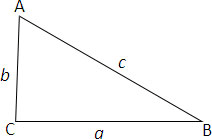
Step: 1

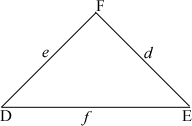
The length c is longer side and the angle opposite to it is angle C.

Step: 2

Cos C = 42+32-522(4)(3)

[Use law of cosines:
Cos C = a2+b2-c22ab.]

Step: 3

Cos C = 024 = 0

Step: 4

∠C = 90^o

Correct Answer is : 90^o

Q2In triangle DEF, if d = 6, e = 15, and f = 22, then find the measure of angle D to the nearest degree.
A. 70^o
B. 60^o
C. 80^o
D. not possible to find

Solutions

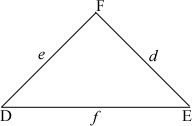
Step: 1

d2 = e2 + f2 - 2ef cos D.

[Law of Cosines.]

Step: 2

Cos D = e2+f2-d22ef.

Step: 3

Cos D = 152+222-622(15)(22)

Step: 4

Cos D ≈ 1.019696

Step: 5

∠D is not possible. Since the cosine of an angle cannot be greater than one.

Step: 6

Triangle cannot be drawn with the given sides.

Correct Answer is : not possible to find

Q3In ΔDEF, if d = 19, e = 19 and f = 20, then find ∠F to the nearest degree.

A. 26^o
B. 66^o
C. 68^o
D. 64^o

Solutions

Step: 1

Cos F = 192+192 -2022(19)(19)

[Use law of cosines:
Cos F = d2+e2-f22de.]

Step: 2

Cos F ≈ 0.446

Step: 3

∠F ≈ 64°

Correct Answer is : 64^o

Q4In ΔPQR, if ∠Q = 75^o, p = 12, q = 17, then find the measure of the angle R to the nearest degree.

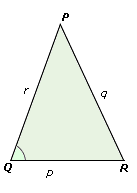
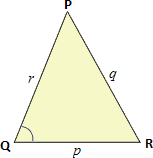
A. 75^o
B. 137^o
C. 43^o
D. 62^o

Solutions

Step: 1

Sin 75o17 = Sin P12

[Use law of Sines: Sin Qq = Sin Pp .]

Step: 2

Sin P = 12 Sin 75o17

Step: 3

Sin P = 0.68

Step: 4

∠P = 43^o (or) 137^o

Step: 5

The measure of 137^o is not possible, since 137^o + 75^o = 212^o and 212^o is greater than 180^o.

Step: 6

So, ∠P = 43^o.

Step: 7

∠R = 180 - (75^o + 43^o)

[Sum of the angle measures in a triangle is 180^o.]

Step: 8

∠R = 62^o

Correct Answer is : 62^o

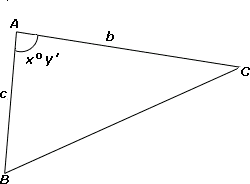
Q5A point A is c cm from B and b cm from C as shown in the figure. If ∠ ABC is x^o, then find the distance between B and C.
[b = 14, c = 20, x = 50,y = 30.]

A. 21.7 cm
B. 16.1 cm
C. 34.3 cm
D. 15.5 cm

Solutions

Step: 1

BC2 = AB2 + AC2 - 2(AB)(AC)) cos∠BAC

[Use law of Cosines.]

Step: 2

BC2 = 14² + 20² - 2(14)(20) cos 50^o30'

Step: 3

BC2 ≈ 239.796320

[Simplify.]

Step: 4

BC = 15.5

[Simplify.]

Step: 5

The distance between B and C is 15.5 cm.

Correct Answer is : 15.5 cm

Q6In ΔABC, if ∠B = 64^o, ∠C = 64^o, and b = 26 units, then find the length of a.

A. 23 units
B. 26 units
C. 20 units
D. 30 units

Solutions

Step: 1

∠A = 180^o - (64^o + 64^o)

[Sum of the measures of angles in a triangle is 180^o.]

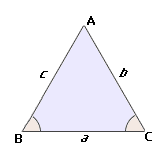
Step: 2

∠A = 52^o

Step: 3

sin 52oa = sin 64o26

[Use law of sines: sin Aa = sin Bb.]

Step: 4

a = 26 sin 52osin 64o = 23 units, to two significant digits.

[Simplify.]

Correct Answer is : 23 units

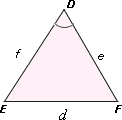
Q7In triangle DEF, if ∠D = 45°, f = 11, and e = 9, then find the length of d.[Round it to the nearest whole number].

A. 21
B. 10
C. 13
D. 8

Solutions

Step: 1

d2 = 11² + 9² - 2(11)(9) cos 45°

[Using law of cosines:
d2 = e2 + f2 - 2ef cos D.]

Step: 2

d² ≈ 62.014

Step: 3

d = 8.

[Simplify using calculator.]

Correct Answer is : 8

Q8In ΔDEF, if d = 28, e = 28, and f = 35, then find ∠F to the nearest degree.

A. 13°
B. 77°
C. 81°
D. 83°

Solutions

Step: 1

Cos F = 282+282-3522(28)(28)

[Use law of cosines:
Cos F = d2+e2-f22de.]

Step: 2

Cos F ≈ 0.2188

Step: 3

∠F ≈ 77°

Correct Answer is : 77°

Q9In ΔABC, if ∠A = 62°, a = 14 in., b = 8 in., then find the length of c to the nearest two significant digits.

A. 14 in.
B. 24 in.
C. 17 in.
D. 16 in.

Solutions

Step: 1

sin 62°14 = sin B8

[Use law of Sines: sin Aa = sin Bb.]

Step: 2

sin B = 8 sin 62°14

Step: 3

sin B = 0.50

[Simplify.]

Step: 4

∠B = 30° or 150°

Step: 5

The measure of 150° is not possible, since 150° + 62° = 212° and 212° is greater than 180°.

Step: 6

So, ∠B = 30°.

Step: 7

∠C = 180° - (62° + 30°) = 88°

Step: 8

sin 88°c = sin 62°14

[Use law of Sines: sin Cc = sin Aa.]

Step: 9

c = 14 sin 88°sin 62° = 16 in.

Correct Answer is : 16 in.

Q10In ΔPQR, if ∠Q = 68°, p = 17 units, and q = 23 units, then what is the measure of ∠R to the nearest degree?

A. 72°
B. 44°
C. 61°
D. 68°

Solutions

Step: 1

Sin P17 = Sin 68°23

[Use law of Sines : sin Pp = sin Qq .]

Step: 2

Sin P = 17 Sin 68°23

Step: 3

Sin P = 0.7

[Simplify.]

Step: 4

∠P = 44° (or) ∠P = 136°

Step: 5

The measure of 136° is not possible, since 136° + 68° = 204° and 204° is greater than 180°.

Step: 6

So, ∠P = 44°.

Step: 7

∠R = 180 - (68^o + 44^o)

[Sum of the angle measures in a triangle is 180^o.]

Step: 8

∠R = 68^o

Correct Answer is : 68°

Q11In ΔABC, if ∠C = 73^o, a = 11 units, c = 17 units, then find ∠B to the nearest degree.
A. 38^o
B. 59^o
C. 142^o
D. 69^o

Solutions

Step: 1

sin A11 = sin 73o17

[Use law of Sines: sin Aa = sin Cc .]

Step: 2

sin A = 11 sin 73o17

Step: 3

sin A = 0.62

Step: 4

∠A = 38^o (or) 142^o

Step: 5

The measure of 142^o is not possible, since 142^o + 73^o = 215^o and 215^o is greater than 180^o.

Step: 6

So, ∠A = 38^o.

Step: 7

∠B = 180 - (38^o + 73^o)

[Sum of the angle measures in a triangle is 180^o.]

Step: 8

∠B = 69^o

Correct Answer is : 69^o

Q12In triangle DEF, ∠D = θ = 35°44′, e = 12.5 units, and f = 17.4 units. What is the length d to four significant digits?

A. 15.42
B. 10.29
C. 10.2637
D. 20.412

Solutions

Step: 1

d2 = 12.52 + 17.42 - 2(12.5)(17.4) cos 35°44′

[Use law of cosines:
d2 = e2 + f2 - 2ef cos D.]

Step: 2

d2 ≈ 105.901

Step: 3

d = 10.29, to four significant digits

Correct Answer is : 10.29

Solved Examples and Worksheet for Law of Sines and Cosines to Solve Triangles

Related Worksheet

Related Topic

HighSchool Math