Solved Examples and Worksheet for Application of the Pythagorean Theorem

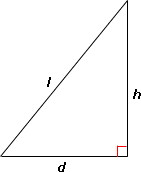
Q1One end of a wire with a length of 20 feet is tied to the top of the pole and the other end is fixed on the ground at a distance of 12 feet from the foot of the pole. What is the height of the pole?

A. 48 feet
B. 16 feet
C. 28 feet
D. 36 feet

Solutions
Share 
Step: 1
d2 + h2 = l2
  [Apply Pythagorean theorem.]
Step: 2
h2 = l2 - d2
  [Subtract d2 from both sides.]
Step: 3
h2 = 202 - 122
  [Substitute l and d.]
Step: 4
= 400 - 144
  [Apply exponents and simplify.]
Step: 5
= 256
  
Step: 6
⇒ h = 256
  [Take square root of both sides.]
Step: 7
= 16
  
Step: 8
Therefore, the height of the pole is 16 feet.
Correct Answer is :   16 feet
Q2Justin walked diagonally across a square garden of side 12 ft from one corner to the opposite corner. How far did he walk?

A. 17.09 ft
B. 18.09 ft
C. 15.85 ft
D. 16.97 ft

Solutions
Share 
Step: 1
Let s be the side of the square garden and d be the distance Justin walked.
Step: 2
All the angles of a square are right angles. So, the diagonal of the square will be the hypotenuse of the right triangle formed by two adjacent sides and the diagonal.
Step: 3
d2 = s2 + s2
  [Apply Pythagorean theorem.]
Step: 4
d2 = 122 + 122
  [Substitute s = 16.]
Step: 5
d2 = 144 + 144 = 288
  [Apply exponents and simplify.]
Step: 6
d = √288 = 16.97
  [Take square root on both sides.]
Step: 7
The total distance Justin walked is 16.97 ft.
Correct Answer is :   16.97 ft
Q3A ladder which is 10 feet long is placed on a wall such that the top of the ladder touches the top of the wall. The bottom of the ladder is 6 feet away from the wall. What is the height of the wall?
A. 11 feet
B. 5 feet
C. 8 feet
D. 14 feet

Solutions
Share 
Step: 1
The length of the ladder l = 10 feet.
Step: 2
The distance from the foot of the ladder to the wall, d = 6 feet.
Step: 3
Let h be the height of the wall.
Step: 4
d2 + h2 = l2
  [Write Pythagorean theorem.]
Step: 5
h2 = l2 - d2
  [Subtract d2 from both sides.]
Step: 6
= 102 - 62
  [Substitute l and h.]
Step: 7
= 100 - 36
  [Apply exponents and simplify.]
Step: 8
= 64
  
Step: 9
h = √64
  [Take square root of both sides.]
Step: 10
= 8
  
Step: 11
Height of the wall = 8 feet.
Correct Answer is :   8 feet
Q4Jim walked diagonally across a square garden with each side measuring 25 ft in length (from one corner to the opposite corner). How far did he walk?
A. 35.47 ft
B. 33.23 ft
C. 35.35 ft
D. 37.47 ft

Solutions
Share 
Step: 1
Let s be the side of the square garden and d be the distance Jim walked.
Step: 2
All the angles of a square are right angles. So, the diagonal of the square will be the hypotenuse of the right triangle formed by two adjacent sides and the diagonal.
Step: 3
d2 = s2 + s2
  [Apply Pythagorean theorem.]
Step: 4
d2 = 252 + 252
  [Substitute s = 25.]
Step: 5
d2 = 625 + 625 = 1250
  [Apply exponents and simplify.]
Step: 6
d = √1250 = 35.35
  [Take square root on both sides.]
Step: 7
The total distance Jim walked is 35.35 ft.
Correct Answer is :   35.35 ft
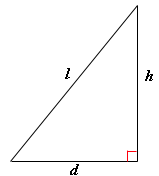
Q5One end of a wire with a length of 26 feet is tied to the top of the pole and the other end is fixed to the ground at a distance of 10 feet from the foot of the pole. What is the height of the pole?


A. 24 feet
B. 34 feet
C. 16 feet
D. 50 feet

Solutions
Share 
Step: 1
Let h be the height of the pole.
Step: 2
d2 + h2 = l2
  [Apply Pythagorean theorem.]
Step: 3
h2 = l2 - d2
  [Subtract d2 from both sides.]
Step: 4
h2 = 262 - 102
  [Substitute l and d.]
Step: 5
= 676 - 100
  [Apply exponents and simplify.]
Step: 6
= 576
  
Step: 7
h = 576
  [Take square root of both sides.]
Step: 8
= 24
  
Step: 9
The height of the pole is 24 feet.
Correct Answer is :   24 feet
Q6Wilma went to an open field to fly a kite. She let out all 150 ft of string and tied it to a stake. Then she walked out on the field until she was directly under the kite, 90 ft from the stake. How high was the kite?
A. 150 ft.
B. 90 ft
C. 100 ft.
D. 120 ft.

Solutions
Share 
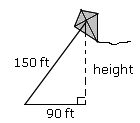
Step: 1
Draw the figure using the data in the question.
Step: 2
Length of the kite string = hypotenuse of a right triangle = 150 ft.
Step: 3
Distance between Wilma and the stake = One leg of the triangle = 90 ft.
Step: 4
Let height of the kite = another leg of the triangle = x ft.
Step: 5
902 + x2 = 1502
  [Apply Pythagorean theorem.]
Step: 6
8100 + x2 = 22500
Step: 7
x2 = 14400
  [Subtract 8100 from each side.]
Step: 8
x = 120
  [Take square roots on both sides.]
Step: 9
Height of the kite = 120 ft.
Correct Answer is :   120 ft.
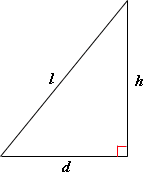
Q7One end of a 20 feet long wire is tied to the top of a pole and the other end is fixed on to the ground at a distance of 12 feet from the foot of the pole. What is the height of the pole?

A. 28 feet
B. 16 feet
C. 36 feet
D. 20 feet

Solutions
Share 
Step: 1
Let h be the height of the pole.
Step: 2
d2 + h2 = l2
  [Apply Pythagorean theorem.]
Step: 3
h2 = l2 - d2
  [Subtract d2 from both sides.]
Step: 4
h2 = 202 - 122
  [Substitute l and d.]
Step: 5
= 400 - 144
  [Apply exponents and simplify.]
Step: 6
= 256
  
Step: 7
h = 256
  [Take square root on both sides.]
Step: 8
= 16
  
Step: 9
The height of the pole is 16 feet.
Correct Answer is :   16 feet
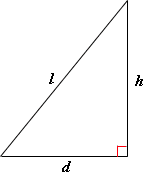
Q8One end of a 10 foot long wire is tied to the top of a pole and the other end is fixed on to the ground at a distance of 6 feet from the foot of the pole. What is the height of the pole?


A. 10 feet
B. 8 feet
C. 14 feet
D. 18 feet

Solutions
Share 
Step: 1
Let h be the height of the pole.
Step: 2
d2 + h2 = l2
  [Apply Pythagorean theorem.]
Step: 3
h2 = l2 - d2
  [Subtract d2 from both sides.]
Step: 4
h2 = 102 - 62
  [Substitute l and d.]
Step: 5
= 100 - 36
  [Apply exponents and simplify.]
Step: 6
= 64
  
Step: 7
h = 64
  [Take square root of both sides.]
Step: 8
= 8
  
Step: 9
The height of the pole is 8 feet.
Correct Answer is :   8 feet
Q9Latif walked diagonally across a square garden with each side measuring 25 m long (from one corner to the opposite corner). How far did he walk?

A. 35.47 m
B. 37.47 m
C. 35.35 m
D. 33.23 m

Solutions
Share 
Step: 1
Let s be the side of the square garden and d be the distance Latif walked.
Step: 2
All the angles of a square are right angles. So, the diagonal of the square will be the hypotenuse of the right triangle formed by two adjacent sides and the diagonal.
Step: 3
d2 = s2 + s2
  [Use Pythagorean theorem.]
Step: 4
d2 = 252 + 252
  [Substitute s = 25.]
Step: 5
d2 = 625 + 625 = 1250
  [Simplify.]
Step: 6
d = 1250 = 35.35
  [Take square root on both sides.]
Step: 7
Hence, the total distance Latif walked is 35.35 m.
Correct Answer is :   35.35 m
Q10Chris walked diagonally across a square garden with each side measuring 27 ft in length (from one corner to the opposite corner). How far did he walk?
A. 33.23 ft
B. 38.18 ft
C. 35.47 ft
D. 37.47 ft

Solutions
Share 
Step: 1
Let s be the side of the square garden and d be the distance Chris walked.
Step: 2
All the angles of a square are right angles. So, the diagonal of the square will be the hypotenuse of the right triangle formed by two adjacent sides and the diagonal.
Step: 3
d2 = s2 + s2
  [Apply Pythagorean theorem.]
Step: 4
d2 = 272 + 272
  [Substitute s = 27.]
Step: 5
d2= 729 + 729 = 1458
  [Simplify.]
Step: 6
d = √1458 = 38.18
  [Take square root on both sides.]
Step: 7
The total distance Chris walked is 38.18 ft.
Correct Answer is :   38.18 ft

HighSchool Math