Solved Examples and Worksheet for Volume of Cones

Q1The height of a right circular cone is 9 cm. If its volume is 432π cm.3, what is the slant height of the cone?

A. 15 cm
B. 24 cm
C. 11 cm
D. 20 cm

Solutions
Share 
Step: 1
Volume of a cone = 13πr2h
  [Formula.]
Step: 2
432π = 13 x π x r2 x 9
  [Substitute the values.]
Step: 3
r2 = 144
  [Simplify.]
Step: 4
Slant height of cone (l) = √(r2 + h2).
Step: 5
= √ (144 + 92)
  [Substitute the values.]
Step: 6
= √ (225) = 15
  [Simplify.]
Step: 7
Slant height of the cone = 15 cm.
Correct Answer is :   15 cm
Q2The circumference of the base of a cone of height 15 in. is 132 in. Find the volume of the cone. [Use π = 227]
A. 6944. in.3
B. 6925. in.3
C. 6930 in.3
D. 6934. in.3

Solutions
Share 
Step: 1
Circumference of the base of a cone = 2πr
  [Formula.]
Step: 2
2πr = 132 in.
  [Since circumference of a cone is 132 in.]
Step: 3
2 x 227 x r = 132
  
Step: 4
r = 21 in.
  [Simplify.]
Step: 5
Volume of the cone = 13πr2h
  [Formula.]
Step: 6
= 13 x 227 x 212 x 15
  [Substitute the values.]
Step: 7
= 6930
  [Simplify.]
Step: 8
Volume of the cone = 6930 in.3.
Correct Answer is :   6930 in.3
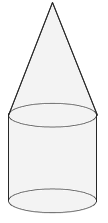
Q3A tent is in the shape of a cylinder with a conical top. The radius of the base of the tent is 8 m. The height of the cylindrical part is 15 m. and that of the conical part is 24 m. Find the volume of air that occupies the tent. (Round the answer to one decimal place.)

A. 4607.1 m3
B. 4637.1 m3
C. 4627.1 m3
D. 4622.1 m3

Solutions
Share 
Step: 1
Volume of cylindrical part = πr2h
  [Formula.]
Step: 2
= 3.14 x 82 x 15
  [Substitute the values.]
Step: 3
= 3014.40
  [Simplify.]
Step: 4
Volume of the cylindrical part = 3014.40 m.3.
Step: 5
Volume of Conical part = 13πr2h
  [Formula.]
Step: 6
= 13 x 3.14 x 82 x 24
  [Substitute the values.]
Step: 7
= 1607.68
  [Simplify.]
Step: 8
Volume of the cone = 1607.68 m.3.
Step: 9
Volume of air that occupies the tent = volume of cylindrical part + volume of conical part
= (1607.68 + 3014.40) m.3 = 4622.08 m.3
  
Step: 10
≈ 4622.1 m.3
  [Round the answer to one decimal place.]
Step: 11
Volume of air that occupies the tent = 4622.1 m.3.
Correct Answer is :   4622.1 m3
Q4The area of the base of a cone is 14 in.2 Its volume is 154 in.3 What is the height of the cone?

A. 43 in.
B. 38 in.
C. 33 in.
D. 28 in.

Solutions
Share 
Step: 1
Volume of a cone = 13πr2h
  [Formula.]
Step: 2
= 13 x πr2 x h
  
Step: 3
Volume of cone = 13 x base area of cone x h
  [The base of a cone is a circle.]
Step: 4
154 = 13 x 14 x h
  [Substitute the values.]
Step: 5
h = 33 in.
  [Multiply each side with 314 .]
Step: 6
Height of the cone = 33 in.
Correct Answer is :   33 in.
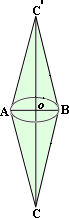
Q5Find the volume of the figure shown, if AB = 8 ft and CO = C′O = 18 ft.


A. 96π ft3
B. 94π ft3
C. 190π ft3
D. 192π ft3

Solutions
Share 
Step: 1
From the figure, the base diameter of each cone, d = AB = 8 ft
and the height of each cone, h = CO = 18 ft.
Step: 2
The base radius of the cone, r = diameter2
= 82
  [Substitute diameter = 8 ft.]
Step: 3
= 4 ft
  
Step: 4
Volume of each cone, V = 13πr2h
  [Formula.]
Step: 5
= 13 × π × 42 × 18
  [Substitute r = 4 and h = 18.]
Step: 6
= 96π ft3
  [Simplify.]
Step: 7
The volume of the figure = 2 × V
  [Since the figure contains two identical cones.]
Step: 8
= 2 × 96π ft3
  [Substitute, V = 96π ft3.]
Step: 9
= 192π ft3
  
Step: 10
The volume of the figure is 192π ft3.
Correct Answer is :   192π ft3
Q6Find the height of the cone whose volume is 720π cm3 and base radius is 12 cm.[Volume of a cone, V = (13)πr2h, where r, h are the radius and height of the cone]

A. 18 cm
B. 13 cm
C. 25 cm
D. 15 cm

Solutions
Share 
Step: 1
Let h be the height of the cone and r be the base radius of the cone.
Step: 2
Volume of the cone, v = (13)πr2h
  [Volume formula.]
Step: 3
The height of the cone, h = 3vπr2
Step: 4
= 3 × 720ππ×122
  [Substitute v = 720π and r = 12.]
Step: 5
= 15 cm
  [Simplify.]
Step: 6
The height of the cone is 15 cm.
Correct Answer is :   15 cm
Q7Find the height of the cone whose volume is 180π cm3 and base radius is 6 cm.

A. 3 cm
B. 15 cm
C. 90 cm
D. 5 cm

Solutions
Share 
Step: 1
Let h be the height of the cone and r be the base radius of the cone.
Step: 2
Volume of the cone, v = (13)πr2h
  [Volume formula.]
Step: 3
The height of the cone, h = 3vπr2
Step: 4
= 3 × 180ππ×62
  [Substitute v = 180π and r = 6.]
Step: 5
= 15 cm
  [Simplify.]
Step: 6
The height of the cone is 15 cm.
Correct Answer is :   15 cm
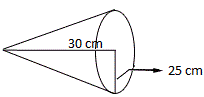
Q8What is the volume of a cone shown below ? (Round the answer to the nearest whole unit)

A. 15872 cm3
B. 19632 cm3
C. 12635 cm3
D. 19631 cm3

Solutions
Share 
Step: 1
Volume of a cone, V = 13πr2h
  [Formulae]
Step: 2
13 × 3.141 × 25 × 25 × 30
  [π = 3.141, r = 25, h = 30 and substituting the values]
Step: 3
19631.25 = 19631 cm 3
  [Simplify and round the answer to the nearest whole]
Step: 4
Therefore, volume of the cone to the nearest whole unit is 19631 cm3.
Correct Answer is :   19631 cm3
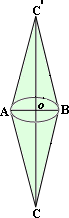
Q9Find the volume of the figure shown, if AB = 8 cm and CO = C'O = 18 cm.

A. 94π cm3
B. 192π cm3
C. 190π cm3
D. 96π cm3

Solutions
Share 
Step: 1
From the figure, the base diameter of each cone, d = AB = 8 cm
and the height of each cone, h = CO = 18 cm.
Step: 2
The base radius of the cone, r = diameter2
= 82
  [Substitute diameter = 8 cm.]
Step: 3
= 4 cm
  [Divide numerator and denominator by 3.]
Step: 4
Volume of each cone, V = 13πr2h
  [Formula.]
Step: 5
= 13 × π × 42 × 18
  [Substitute r = 4 and h = 18.]
Step: 6
= 96π cm3
  [Simplify.]
Step: 7
The volume of the figure = 2 × V
  [Since the figure contains two identical cones.]
Step: 8
= 2 × 96π cm3
  [Substitute, V = 96π cm3.]
Step: 9
= 192π cm3
  
Step: 10
The volume of the figure is 192π cm3.
Correct Answer is :   192π cm3
Q10Find the height of the cone whose volume is 720π cm3 and base radius is 12 cm.


A. 20 cm
B. 25 cm
C. 15 cm
D. 18 cm

Solutions
Share 
Step: 1
Let h be the height of the cone and r be the base radius of the cone.
Step: 2
Volume of the cone, v = (13)πr2h
  [Volume formula.]
Step: 3
The height of the cone, h = 3vπr2
Step: 4
= 3×720ππ×122
  [Substitute v = 720π and r = 12.]
Step: 5
= 15 cm
  [Simplify.]
Step: 6
The height of the cone is 15 cm.
Correct Answer is :   15 cm

HighSchool Math