Solved Examples and Worksheet for Transformations

Q1Translate point A(-3, 2) right 4 units. What are the coordinates of its image A'?


A. (-3, -2)
B. (-1, 2)
C. (0, 3)
D. (1, 2)

Solutions
Share 
Step: 1
Count to the right 4 units from point A(-3, 2).
Step: 2
Graph A'.
Step: 3
The coordinates of A' are (1, 2).
Correct Answer is :   (1, 2)
Q2Translate the point A(- 2, 2) down 4 units and left 2 units. What are the coordinates of its image A′?


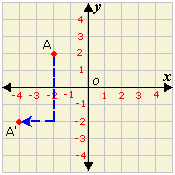
A. (4, - 2)
B. (- 4, 2)
C. (- 4, - 4)
D. (- 4, - 2)

Solutions
Share 
Step: 1
Count down 4 units and left 2 units from the point A.
Step: 2
Graph A′.
Step: 3
The coordinates of the image A′are (- 4, - 2).
Correct Answer is :   (- 4, - 2)
Q3A point P (x, y) is translated 3 units left and 2 units down. Identify a rule for the translation of P.

A. (x, y) → (3, 2)
B. (x, y) → (x + 3, y + 2)
C. (x, y) → (x - 3, y - 2)
D. None of the above

Solutions
Share 
Step: 1
The x and y coordinates of its image P′ become (x - 3) and (y - 2), respectively.
  [The point P (x, y) is moved 3 units to left and 2 units down.]
Step: 2
So, the rule for the translation is (x, y) → (x - 3, y - 2).
Correct Answer is :   (x, y) → (x - 3, y - 2)
Q4Identify a rule for the translation, P (5, 5) → P′(- 2, 9).
A. (x, y) → (7, 4)
B. (x, y) → (x + 7, y - 4)
C. (x, y) → (x - 7, y + 4)
D. None of the above

Solutions
Share 
Step: 1
The x-coordinate of the image P′ is negative.
Step: 2
So, the point P has been translated to the left.
Step: 3
Number of units, it has been translated left = 5 - (- 2) = 7 units
Step: 4
The y-coordinate of the image P′ is greater than that of the point P.
Step: 5
So, the point P has been translated up.
Step: 6
Number of units, it has been translated up = 9 - 5 = 4 units
Step: 7
So, the rule for the translation is (x, y) → (x - 7, y + 4).
Correct Answer is :   (x, y) → (x - 7, y + 4)
Q5What is the equation of the image of line y = 6x + 5, if it has been translated 3 units to the left and 3 units up?

A. y = 26
B. y = 6x + 26
C. y = 6x - 26
D. y = 6x

Solutions
Share 
Step: 1
y = 6x + 5
  [Original line equation.]
Step: 2
The line has been translated 3 units left and 3 units up.
Step: 3
Since the line has translated left 3 units and up 3 units, the rule for the translation is (x, y) → (x + 3, y - 3).
Step: 4
(y - 3) = 6(x + 3) + 5
  [Replace x with (x + 3) and y with (y - 3).]
Step: 5
y - 3 = 6x + 18 + 5
  [Distribute.]
Step: 6
y - 3 = 6x + 23
  
Step: 7
y = 6x + 26
  [Simplify.]
Step: 8
So, equation of the image of the line is y = 6x + 26.
Correct Answer is :   y = 6x + 26
Q6What is the rule to describe the translation, P (5, 3) → P′ (7, - 2)?
A. (x, y) → (x - 2, y - 5)
B. (x, y) → (x + 2, y - 5)
C. (x, y) → (x - 2, y + 5)
D. (x, y) → (x + 2, y + 5)

Solutions
Share 
Step: 1
The x-coordinate of the image P′ is greater than that of the point P.
Step: 2
So, the point P has been translated to the right.
Step: 3
Number of units, it has been translated right = 7 - 5 = 2 units.
Step: 4
The y-coordinate of the image P′ is less than that of the point P.
Step: 5
So, the point P has been translated down.
Step: 6
Number of units, it has been translated down = 3 - (- 2) = 5 units.
Step: 7
So, the rule is (x, y) → (x + 2, y - 5).
Correct Answer is :   (x, y) → (x + 2, y - 5)
Q7Translate the point C (- 1, 2), 3 units down and 5 units right. What are the coordinates of its image C′ ?

A. (- 1, 2)
B. (4, - 1)
C. (2, 1)
D. (1, - 2)

Solutions
Share 
Step: 1
When (- 1, 2) is translated 3 units down, the y-coordinate becomes - 1, but the x-coordinate remains same.Then the point C(- 1,2) is translated to the point(- 1,- 1).
Step: 2
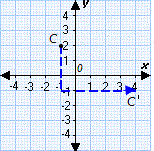
After translating (- 1,- 1) to 5 units right, the x-coordinate of the point becomes 4, but the y-coordinate remains same.
Step: 3
So, the coordinates of the new point C′ are (4, - 1).
Correct Answer is :   (4, - 1)
Q8The coordinates of a point are (- 2, 3) and they are moved to coordinates (2, 3). Identify the steps that can be used for the translation.
A. Move 4 units left.
B. Move 2 units right.
C. Move 4 units right.
D. none of these

Solutions
Share 
Step: 1
The coordinates before translation and after translation are (- 2, 3) and (2, 3).
Step: 2
The x-coordinate after translation is greater than that before translation but the y-coordinate is not changed. So, the translation is towards right.
Step: 3
Translation = 2 - (- 2) = 2 + 2 = 4 units right.
Step: 4
So, move 4 units right from (- 2, 3) to reach (2, 3).
Correct Answer is :   Move 4 units right.
Q9What are the coordinates of the point P (- 2, - 4) when reflected over the line x = 4?

A. (- 6, 4)
B. (6, 4)
C. (10, - 4)
D. None of the above

Solutions
Share 
Step: 1
When a point is reflected over a vertical line the y-coordinate remains the same.
Step: 2
The point P(- 2, - 4) is reflected over the line x = 4.
Step: 3
The distance of the point from the line x = 4 is 2 + 4 = 6.
Step: 4
So, the image of the point will be 6 units away from the line x = 4.
Step: 5
The x-coordinate of the image of the point with respect to the coordinate axes = 6 + 4 = 10.
Step: 6
So, the coordinates of the image of the point P(- 2, - 4) along x = 4 are (10, - 4).
Correct Answer is :   (10, - 4)
Q10What are the coordinates of a point W (- 2, - 2) when reflected over the line y = 5?

A. (2, 7)
B. (- 2, - 7)
C. (2, 12)
D. (- 2, 12)

Solutions
Share 
Step: 1
When a point is reflected over a horizontal line, the x-coordinate remains the same.
  [The line y = 5 will be parallel to the x-axis.]
Step: 2
The point W (- 2, - 2) is reflected over the line y = 5.
Step: 3
The distance of the point (- 2, - 2), from the line y = 5 is 2 + 5 = 7 units
Step: 4
So, the image of the point will be 7 units away from the line y = 5.
Step: 5
The y-coordinate of the image = 7 + 5 = 12
Step: 6
So, the coordinates of the image are (- 2, 12).
Correct Answer is :   (- 2, 12)
Q11What are the coordinates of point C(2, 4) after rotating 180o about the origin in the counter clockwise direction?
A. (-2, 4)
B. (2, 4)
C. (4, 2)
D. (-2, -4)

Solutions
Share 
Step: 1
When point is rotated by 180o, only the signs of the x and the y-coordinates will be interchanged.
Step: 2
Represent the horizontal and the vertical distances of the point P(2, 4) as a rectangle.
Step: 3
Now tilt the rectangle by 180o as the point has to be rotated by 180o.
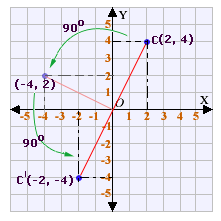
Step: 4
The coordinates of point C after rotating 180o are C'(-2, -4).
  [Observe that the signs of the x and the y-coordinates are interchanged.]
Correct Answer is :   (-2, -4)
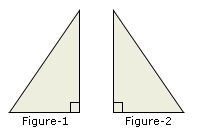
Q12Which transformation should be used to change the Figure-1 to Figure-2?

A. Reflection
B. Translation
C. Rotation
D. Dilation

Solutions
Share 
Step: 1
Figure-2 represents the mirror image of Figure-1.
Step: 2
The transformation used in the Figure-1 to change as Figure-2 is 'reflection'.
Step: 3
So, the correct choice is reflection.
Correct Answer is :   Reflection
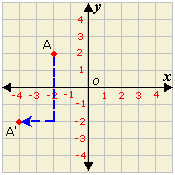
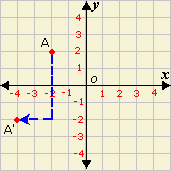
Q13Translate the point A (- 2, 2) down 4 units and left 2 units. What are the coordinates of its image A′?


A. (- 4, - 4)
B. (- 4, - 2)
C. (4, - 2)
D. (- 4, 2)

Solutions
Share 
Step: 1
Count down 4 units and left 2 units from the point A.
Step: 2
Graph A′.
Step: 3
The coordinates of the image A′ are (- 4, - 2).
Correct Answer is :   (- 4, - 2)
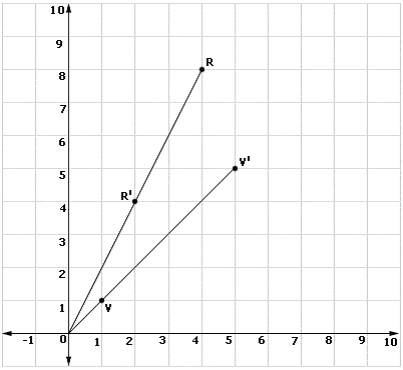
Q14Explain the dilations of R and V in the picture.

A. R dilated by scale factor 12, V dilated by scale factor 5, center of dilation (0, 0)
B. R dilated by scale factor 5, V dilated by scale factor 12, center of dilation (0, 0)
C. R increased by 5 times, V reduced by 5 times
D. None of the above

Solutions
Share 
Step: 1
R (4, 8) is mapped to R′ (2, 4). Scale factor is 12and center (0, 0).
Step: 2
V (1, 1) is mapped to V′(5, 5). Scale factor is 5 and center (0, 0).
Correct Answer is :   R dilated by scale factor 12, V dilated by scale factor 5, center of dilation (0, 0)
Q15What are the coordinates of the point P (3, 4) when rotated by 180° in the counter clockwise direction about the origin?

A. P (- 3, 4)
B. P (3, 4)
C. P (- 3, - 4)
D. P (3, - 4)

Solutions
Share 
Step: 1
Represent the point P (3, 4) on the coordinate plane.
Step: 2
The point P (3, 4) is rotated counter clockwise by 180° as shown in the figure.
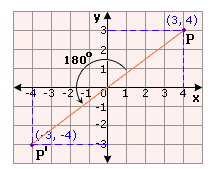
Step: 3
The coordinates of the point P after rotating 180° are P' (- 3, - 4).
Correct Answer is :   P (- 3, - 4)

HighSchool Math