Angle Sum Theorem of a Triangle-Gr 8-Solved Examples

Solved Examples and Worksheet for Angle Sum Theorem of a Triangle

Q1What are the angles of a triangle which are in the ratio 4 : 5 : 6?
A. 58^o, 81^o, 77^o
B. 38^o, 55^o, 72^o
C. 48^o, 60^o, 72^o
D. 96^o, 60^o, 97^o

Solutions

Step: 1

Let 4x, 5x and 6x be the angles.

Step: 2

4x + 5x + 6x = 180^o

[Triangle angle sum theorem.]

Step: 3

15x = 180^o
x = 180°15
x = 12^o

[Divide each side by 15.]

Step: 4

So, 4x = 4 × 12^o = 48^o
5x = 5 × 12^o = 60^o
6x = 6 × 12^o = 72^o

[Substitute x = 12^o.]

Step: 5

The angles of the triangle are 48^o, 60^o and 72^o .

Correct Answer is : 48^o, 60^o, 72^o

Q2If m∠A + m∠B = 90, then what all can be concluded from this?
(i) One arm of ∠A and one arm of ∠B are perpendicular
(ii). ∠A and ∠B are complementary.
(iii). m∠A = 90 - m∠B
(iv) m∠B = 90 - m∠A
(v). ∠A and ∠B cannot be the angles of the same triangle.

A. (i), (ii) and (v)
B. (ii), (iii), (iv) and (v)
C. All statements
D. (ii), (iii) and (iv)

Solutions

Step: 1

The two angles can be with two different arms. Statement (i) need not be correct.

Step: 2

The two angles can be the angles of the same triangle since sum of the angles of a triangle is 180 degrees.

Step: 3

(ii), (iii) and (iv) are correct.

Correct Answer is : (ii), (iii) and (iv)

Q3Find the value of 2y + 3z.

A. 200
B. 300
C. 350
D. 250

Solutions

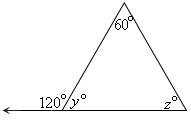
Step: 1

y + 120 = 180

[Linear pair.]

Step: 2

y = 180 - 120 = 60

[Simplify.]

Step: 3

The sum of the measures of the angles of a triangle is 180.

[Triangle angle sum theorem.]

Step: 4

60 + y + z = 180

[From step 3.]

Step: 5

60 + 60 + z = 180

[Substitute 60 for y.]

Step: 6

z = 180 - 120 = 60

[Simplify.]

Step: 7

So, 2y + 3z = 120 + 180 = 300

[Substitute 60 for y and z.]

Correct Answer is : 300

Q4Find the values of x and y.

A. 72 and 36
B. 36 and 72
C. 36 and 36
D. 72 and 72

Solutions

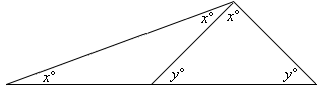
Step: 1

The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles.

[Exterior angle theorem.]

Step: 2

y = 2x

[From step 1.]

Step: 3

The sum of the measure of the angles of a triangle is 180.

[Triangle angle-sum theorem.]

Step: 4

x + y + y = 180

[From step 3.]

Step: 5

x + 2x + 2x = 180

[Substitute y = 2x.]

Step: 6

5x = 180 ⇒ x = 36

[Simplify.]

Step: 7

y = 2x ⇒ 2(36) = 72

[From step 2.]

Step: 8

Hence the value of x is 36 and y is 72.

Correct Answer is : 36 and 72

Q5If the angles of a triangle are in the ratio of 2 : 4 : 6, find the largest angle.

A. 90°
B. 120°
C. 60°
D. 100°

Solutions

Step: 1

Since the measures of the angles of the triangle are in the ratio 2: 4: 6, the measures of the angles of triangle can be taken as 2x, 4x and 6x.

Step: 2

The sum of the measure of angles of a triangle is 180.

[Triangle angle sum theorem.]

Step: 3

2x + 4x + 6x =180

[ From steps 1 and 2 ]

Step: 4

12x= 180

[Simplify]

Step: 5

x = 15

[solve for x]

Step: 6

The measures of the angles of triangle are,

Step: 7

2x = 2(15) = 30,

Step: 8

4x=4(15) = 60 and

Step: 9

6x = 6(15) = 90

Step: 10

Therefore, the largest angle of a triangle = 90°.

Correct Answer is : 90°

Q6The measures of angles of a triangle are perfect squares. Find the difference between the largest and the smallest angles.
A. 84°
B. 6°
C. 36°
D. 48°

Solutions

Step: 1

The sum of all the three angles in a triangle is 180°.

[Angle sum theorem of a triangle.]

Step: 2

The measures of angles of a triangle are perfect squares.

[Given.]

Step: 3

If the angles of a triangle are a°, b°, and c°, then a + b + c = 180°, where a, b, and c are perfect squares.

Step: 4

Let the angles be a = 16°, b = 64°, and c = 100°.

Step: 5

⇒ 16 + 64 + 100 = 180

[16 = 4², 64 = 8², and 100 = 10².]

Step: 6

Here, the largest angle is 100 and the smallest angle is 16.

Step: 7

So, the difference between the largest and the smallest angles = 100 - 16 = 84°.

Correct Answer is : 84°

Q7If x = 62°, then find the missing angle shown in the figure.

A. 28°
B. 45°
C. 36°
D. cannot be determined

Solutions

Step: 1

The sum of all the angle measures of a triangle is 180°.

Step: 2

90° + 62° + y° = 180°

[Equate the sum of angles of the triangle to 180°.]

Step: 3

152° + y° = 180°

[Add.]

Step: 4

y° = 28°

[Subtract 152° from each side.]

Correct Answer is : 28°

Q8What are the measures of the angles of a triangle, if they are in the ratio 5 : 6 : 7 ?

A. 100°, 60°, 95°
B. 40°, 55°, 70°
C. 60°, 81°, 75°
D. 50°, 60°, 70°

Solutions

Step: 1

Let 5x, 6x and 7x be the angles.

Step: 2

Sum of the measures of the angles in a triangle = 180°

Step: 3

5x + 6x + 7x = 180°
18x = 180°
x = 180°18
x = 10°

[Divide each side by 18.]

Step: 4

5x = 5 × 10° = 50°
6x = 6 × 10° = 60°
7x = 7 × 10° = 70°

[Substitute x = 10° .]

Step: 5

The measures of the angles are 50°, 60° and 70° .

Correct Answer is : 50°, 60°, 70°

Q9Find the value of x.

A. 32
B. 42
C. 29
D. 34

Solutions

Step: 1

The sum of the measures of the angles of a triangle is 180°.

[Triangle angle sum theorem.]

Step: 2

x° + (2x + 4)°+ (3x + 2)° = 180°.

Step: 3

6x = 174.

[Simplify.]

Step: 4

x = 29.

[Solve for x.]

Correct Answer is : 29

Q10The measures of angles of ΔPQR are 2x, 3x and 4x. Find the value of x.
A. 324°
B. 400°
C. 256°
D. 200°

Solutions

Step: 1

The measures of angles of ΔPQR are 2x, 3x and 4x.

[Given.]

Step: 2

The sum of the measure of angles of a triangle is 180°.

[Triangle angle sum theorem.]

Step: 3

2x + 3x + 4x = 180°

Step: 4

9x = 180°

[Simplify.]

Step: 5

x = 1809 = 20°

[Simplify.]

Step: 6

x = (20)² = 400°

[Squaring on both sides.]

Step: 7

Therefore, x = 400°.

Correct Answer is : 400°

Q11The ratio of the angle measures in a triangle is 2 : 3 : 5. The triangle is ______.
A. an obtuse angled triangle
B. a right triangle
C. an equilateral triangle
D. an isosceles triangle

Solutions

Step: 1

Since the measures of the angles of the triangle are in the ratio 2 : 3 : 5, the measures of the angles of it can be taken as 2x, 3x and 5x.

Step: 2

The sum of the measure of angles of a triangle is 180°.

[Triangle angle sum theorem.]

Step: 3

2 x + 3 x + 5 x = 180 °

Step: 4

10x = 180°

[Simplify.]

Step: 5

x = 18010 = 18°

[Simplify.]

Step: 6

2 x = 2 × 18° = 36°,
3 x = 3 × 18× = 54° and 5 x = 5 × 18° = 90°

Step: 7

So, the measures of the angles of the triangle are 36° , 54° and 90° and hence the triangle is right triangle.

Correct Answer is : a right triangle

Q12Find the value of x in the figure shown.

A. 48°
B. 42°
C. 46°
D. 36°

Solutions

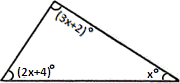
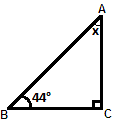
Step: 1

The sum of all the angle measures of a triangle is 180°.

Step: 2

90° + 44° + x = 180°

[Equate the sum of angles of the triangle to 180°.]

Step: 3

134° + x = 180°

[Add.]

Step: 4

x = 180° - 134°

[Simplify.]

Step: 5

Therefore, x = 46°.

Correct Answer is : 46°

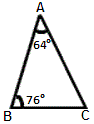
Q13In triangle ABC, ∠BAC = 64° and ∠ABC = 76°. What is the measure of ∠BCA?

A. 46°
B. 30°
C. 50°
D. 40°

Solutions

Step: 1

The sum of all the angle measures of a triangle is 180° .

Step: 2

So, ∠BAC + ∠ABC + ∠BCA = 180°.

Step: 3

∠BCA + 64° + 76° = 180°

[Substitute the given values of ∠BAC and ∠ABC.]

Step: 4

∠ BCA + 140° = 180°

Step: 5

∠BCA = 180° - 140°

[Simplify.]

Step: 6

Therefore, the measure of ∠BCA is 40°.

Correct Answer is : 40°

Q14In triangle ABC, ∠BAC = 64° and ∠ABC = 76°. What is the measure of ∠BCA?

A. 50°
B. 40°
C. 30°
D. 46°

Solutions

Step: 1

The sum of all the angle measures of a triangle is 180°.

Step: 2

∠BCA + 64° + 76° = 180°

Step: 3

∠BCA + 140° = 180°

Step: 4

∠BCA = 180° - 140°

[Simplify.]

Step: 5

Therefore, the measure of ∠BCA is 40°.

Correct Answer is : 40°

Solved Examples and Worksheet for Angle Sum Theorem of a Triangle

Related Worksheet

Related Topic

HighSchool Math