Solved Examples and Worksheet for Exterior Angle Theorem
Step: 1
[Sum of the interior angles of a triangle is 180°.]
Step: 2
55° + 65° + ∠
[Substitute.]
Step: 3
120° + ∠
[Add.]
Step: 4
[Subtract 120 on both the sides.]
Step: 5
[Angle made by a straight line is 180°.]
Step: 6
[Substitute.]
Step: 7
[Subtract 60 on both the sides.]
Step: 8
So, the value of x
Correct Answer is : 120°
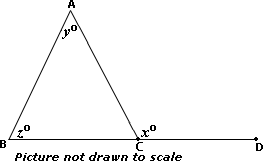
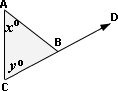
Step: 1
[Linear pair.]
Step: 2
Step: 3
The sum of the measures of the angles of a triangle is 180.
[Triangle angle sum theorem.]
Step: 4
[From step 3.]
Step: 5
[Simplify.]
Step: 6
So, z y
Correct Answer is : 150
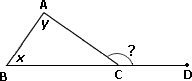
A. 40
B. 126
C. 140
D. 94
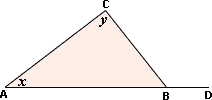
Step: 1
In ΔA B C m ∠ A B C m ∠ B A C
Step: 2
Since side B C D ∠ A C B ∠ A C D
Step: 3
The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles.
[Exterior angle theorem.]
Step: 4
[From step 3.]
Step: 5
54 + 86 = m ∠ A C D
[Substitute the values of ∠ ∠
Step: 6
[Simplify.]
Step: 7
So, the measure of the marked exterior angle of the triangle is 140.
Correct Answer is : 140
A. 108°
B. 18°
C. 92°
D. 72°
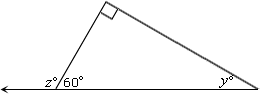
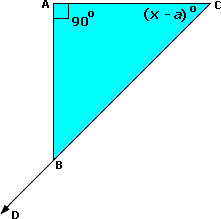
Step: 1
From the figure, ∠ B A C ∠ A B D
Step: 2
The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles.
[Exterior angle theorem.]
Step: 3
[From step 2.]
Step: 4
90° + (x
[Substitute.]
Step: 5
36° + x
Step: 6
[Subtract 36 from both sides.]
Step: 7
So, the value of x
Correct Answer is : 72°
A. 73°
B. 136°
C. 44°
D. 63°
Step: 1
From the figure, ∠ ∠
Step: 2
The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles.
[Exterior Angle Theorem.]
Step: 3
[From step 2.]
Step: 4
63° + y
[Substitute.]
Step: 5
[Subtract.]
Step: 6
So, the measure of y
Correct Answer is : 73°
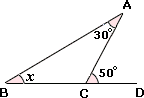
Step: 1
If one side of a triangle is produced, then the exterior angle so formed is equal to the sum of the interior opposite angles.
Step: 2
Step: 3
Step: 4
50° = 30° + x
Step: 5
Step: 6
Step: 7
Therefore, the measure of x
Correct Answer is : 20°
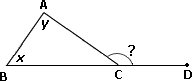
A. 37°
B. 144°
C. 141°
D. 91°
Step: 1
In ΔABC, ∠ ∠
Step: 2
Since side BC is extended to the point D, exterior angle of ∠ ∠
Step: 3
The measure of each exterior angle of a triangle equals the sum of the measures of its two remote interior angles.
[Exterior angle theorem.]
Step: 4
[From step 3.]
Step: 5
52° + 89° = ∠
[Substitute the values of ∠ ∠
Step: 6
[Simplify.]
Step: 7
So, the measure of the marked exterior angle of the triangle is 141°.
Correct Answer is : 141°
- Parallel Lines and Transversals-Gr 8-Solved Examples
- Angle Sum Theorem of a Triangle-Gr 8-Solved Examples
- Pythagorean Theorem-Gr 8-Solved Examples
- Distance Between Two Points-Gr 8-Solved Examples
- Transformations-Gr 8-Solved Examples
- Volume of Cylinders-Gr 8-Solved Examples
- Volume of Cones-Gr 8-Solved Examples
- Volume of a Sphere-Gr 8-Solved Examples
Related Worksheet
- Exterior Angle