Solved Examples and Worksheet for Parallel Lines and Transversals
Step: 1
[Alternate Interior Angles
Theorem.]
Step: 2
[Simplify.]
Step: 3
[Same-Side Interior Angles Theorem.]
Step: 4
35° + x
[Substitute.]
Step: 5
[Simplify.]
Correct Answer is : 145°
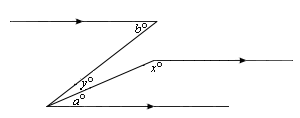
Step: 1
[∠
Step: 2
[Angle Addition Postulate.]
Step: 3
140° + m ∠
[Substitute.]
Step: 4
[Simplify.]
Step: 5
[Alternate Interior Angles Theorem.]
Step: 6
[Substitute.]
Correct Answer is : 40°
A. 13
B. 52
C. 106
D. 117
E. 128
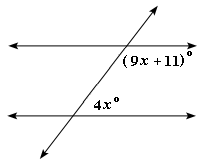
Step: 1
The two labeled angles are supplementary angles and hence their sum is equal to 180o.
Step: 2
4x x
Step: 3
13x
Step: 4
13x ⇒ x
Correct Answer is : 13
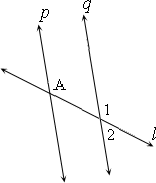
A.
B.
C.
D.
Step: 1
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
[Corresponding angles postulate.]
Step: 2
[Corresponding angles.]
Step: 3
[Linear Pair.]
Step: 4
125° + ∠
Step: 5
Step: 6
Step: 7
Hence m ∠ m ∠
Correct Answer is : m ∠ m ∠
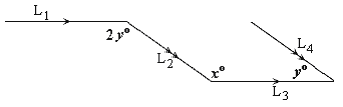
Step: 1
From the figure, x y ⇒ 1 2 x y
[Alternate angles.]
Step: 2
From the figure, x y
[Supplementary angles.]
Step: 3
[From step 1 and step 2.]
Step: 4
[Solve for x
Correct Answer is : 120
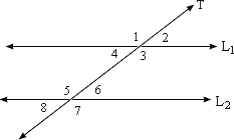
A. complementary.
B. congruent.
C. supplementary.
D. none of the above
Step: 1
[Same-Side Interior Angles Theorem.]
Step: 2
[Step 1.]
Correct Answer is : supplementary.
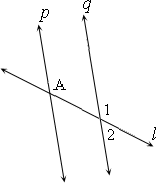
A.
B.
C.
D.
Step: 1
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
[Corresponding angles postulate.]
Step: 2
[Corresponding angles.]
Step: 3
[Adjacent angles.]
Step: 4
135° + ∠
Step: 5
Step: 6
Step: 7
Hence m ∠ m ∠
Correct Answer is : m ∠ m ∠
Step: 1
[∠
Step: 2
[Angle Addition Postulate.]
Step: 3
130 + m ∠
[Substitute.]
Step: 4
[Simplify.]
Step: 5
[Alternate Interior Angles Theorem.]
Step: 6
[Substitute.]
Correct Answer is : 50
Step: 1
[∠
Step: 2
[Angle Addition Postulate.]
Step: 3
160 + m ∠
[Substitute.]
Step: 4
[Simplify.]
Step: 5
[Alternate Interior Angles Theorem.]
Step: 6
[Substitute.]
Correct Answer is : 20
A.
B.
C.
D.
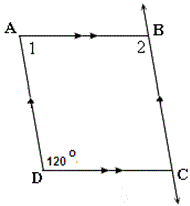
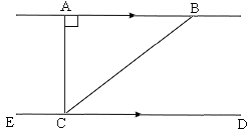
Step: 1
If two parallel lines are cut by a transversal, then the pairs of Same-side interior angles are supplementary.
[AB ¯ DC ¯ AD ¯
Step: 2
∠1 + 120° = 180°
[Same - side interior angles theorm.]
Step: 3
∠1 = 180° - 120° = 60°
[Simplify.]
Step: 4
[Same - side interior angles theorm.]
Step: 5
60 + m
[From step 3.]
Step: 6
[Simplify.]
Step: 7
So, m m
Correct Answer is : m m
A.
B.
C.
D.
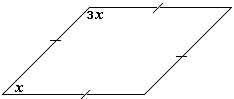
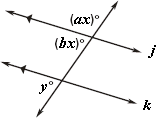
Step: 1
10x x
[Adjacent angles.]
Step: 2
12x
Step: 3
Step: 4
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
[Corresponding angles postulate .]
Step: 5
[From step 4.]
Step: 6
Step: 7
So, x y
Correct Answer is : x y
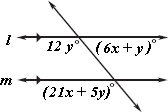
A.
B.
C.
D.
Step: 1
If two parallel lines are cut by a transversal, then the corresponding angles are congruent.
[Corresponding angles postulate.]
Step: 2
12y x y
[Corresponding angles.]
Step: 3
7y x ⇒ y x
[Simplify.]
Step: 4
12y x y
[Adjacent angles.]
Step: 5
13y x
[Simplify.]
Step: 6
13(3x x ⇒ x
[Substitute y x
Step: 7
[Simplify.]
Step: 8
[From step 3.]
Step: 9
So, the values of x y
Correct Answer is : x y
A.
B.
C.
D.
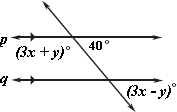
Step: 1
From the data, one of the large angles is (3x y
Step: 2
From the data, two of the small angles are 40° and (3x y
Step: 3
If a transversal intersects two or more parallel lines, all small angles are equal.
Therefore, 3x y
Therefore, 3
Step: 4
If a transversal intersects two or more parallel lines, then sum of small angle and large angle equals straight angle.
Therefore, 3x y
3x y
Therefore, 3
3
Step: 5
Now, add equation (1) and equation (2) and solve for x
6x
x
6
Correct Answer is : x
A. 30
B. 150
C. 330
D. 105
Step: 1
m∠
[∠
Step: 2
m∠ ∠
[Angle Addition Postulate.]
Step: 3
150 + m∠
[Substitute.]
Step: 4
m∠
[Simplify.]
Step: 5
m∠ ∠
[Alternate Interior Angles Theorem.]
Step: 6
m∠
[Substitute.]
Correct Answer is : 30
- Angle Sum Theorem of a Triangle-Gr 8-Solved Examples
- Exterior Angle Theorem-Gr 8-Solved Examples
- Pythagorean Theorem-Gr 8-Solved Examples
- Distance Between Two Points-Gr 8-Solved Examples
- Transformations-Gr 8-Solved Examples
- Volume of Cylinders-Gr 8-Solved Examples
- Volume of Cones-Gr 8-Solved Examples
- Volume of a Sphere-Gr 8-Solved Examples