Solved Examples and Worksheet for Distance Between Two Points

Q1In a coordinate plane, L is at (-5, -4) and M is at (-8, -5). Find the distance between L and M.
A. 3.16 units
B. 4.16 units
C. 6.16 units
D. 5.16 units

Solutions
Share 
Step: 1
Distance, d = √[(x2 - x1)2 + (y2 - y1)2]
  [Use the distance formula.]
Step: 2
d = √[(-8 - (-5))2 + (-5 - (-4))2]
  [Replace (x2, y2) with (-8, -5) and (x1, y1) with (-5, -4).]
Step: 3
d = √[(-3)2 + (-1)2]
  [Subtract.]
Step: 4
d = √10
  [Simplify.]
Step: 5
d ≈ 3.16
  [Find the positive square root.]
Step: 6
So, distance between L and M = 3.16 units.
Correct Answer is :   3.16 units
Q2The distance between A and B is 10 units. Which among the following can be the ordered pair for B, if A is at (-5, 2)?

A. (5, 2)
B. (6, 2)
C. (5, 3)
D. None of the above

Solutions
Share 
Step: 1
The distance between A and B is 10 units.
Step: 2
Distance d = √[(x2 - x1)2 + (y2 - y1)2]
  [Use the distance formula.]
Step: 3
Distance between (-5, 2) and (6, 2) is √[(6 - (-5))2 + (2 - 2)2] = √(112 + 02) = √(121 + 0) =√121 ≠ 10
Step: 4
Distance between (-5, 2) and (5, 3) is √[(5 - (-5))2 + (3 - 2)2] = √(102 + (1)2) = √(100 + 1) =√101 ≠ 10
Step: 5
Distance between (-5, 2) and (5, 2) is √[(5 - (-5))2 + (2 - 2)2] = √(102 + 02) = √(100 + 0) =√100 = 10.
Step: 6
The coordinates in choices B and C are at a distance other than 10 units from the point A.
Step: 7
The point (5, 2) is at a distance of 10 units from A.
Step: 8
So, the coordinates of B are (5, 2).
Correct Answer is :   (5, 2)
Q3The distance between A(5, 6) and B(3, x) is 2√2 units. Find the coordinates of B.
A. (3, 4)
B. (3, 8)
C. Either A or B
D. None of the above

Solutions
Share 
Step: 1
The distance between (x1, y1) and (x2, y2) = d = √[(x2 - x1)2 + (y2 - y1)2]
  [Use the distance formula.]
Step: 2
Distance between AB, d = √[(3 - 5)2 + (x - 6)2)]
  [Replace (x1, y1) with (5, 6) and (x2, y2) with (3, x).]
Step: 3
d = √[(-2)2 + (x - 6)2]
  [Subtract.]
Step: 4
d = √[4 + (x - 6)2]
  [Simplify.]
Step: 5
d = √[4 + x2 + 36 - 12x]
  [Apply exponents.]
Step: 6
= √(x2 - 12x + 40)
  
Step: 7
The distance between A and B is 2√2 units.
Step: 8
√(x2 - 12x + 40) = 2√2
  [Equate distances.]
Step: 9
x2 - 12x + 40 = (2√2)2 = 8
  [Squaring on both sides.]
Step: 10
x2 - 12x + 32 = 0
  [Write in general form.]
Step: 11
(x - 4)(x - 8) = 0
  [Factorize.]
Step: 12
x = 4 or x = 8
  
Step: 13
The coordinates of B are either (3, 4) or (3, 8)
  [Substitute x values.]
Correct Answer is :   Either A or B
Q4Find the distance between P (3, 4) and Q (5, 5).

A. 3.23 units
B. 5.23 units
C. 4.23 units
D. 2.23 units

Solutions
Share 
Step: 1
Distance d = √[(x2 - x1) 2 + (y2 - y1) 2]
  [Use the distance formula.]
Step: 2
d = √[(5 - 3)2 + (5 - 4)2]
  [Replace (x2, y2) with (5, 5) and (x1, y1) with (3, 4).]
Step: 3
d = √[22 + 12]
  [Subtract.]
Step: 4
d = √5
  [Simplify.]
Step: 5
d ≈ 2.23
  [Find the positive square root.]
Step: 6
The distance between, P (3, 4) and Q (5, 5) is 2.23 units.
Correct Answer is :   2.23 units
Q5Find the distance between A (5, -3) and B (8, -5).

A. 6.60 units
B. 4.60 units
C. 3.60 units
D. 5.60 units

Solutions
Share 
Step: 1
Distance between two points d = √[(x2 - x1) 2 + (y2 - y1) 2]
  [Use the distance formula.]
Step: 2
d = √[(8 - 5)2 + (-5 - (-3))2]
  [Replace (x2, y2) with (8, -5) and (x1, y1) with (5, -3).]
Step: 3
d = √[(3)2 + (-2)2]
  [Subtract.]
Step: 4
d = √13
  [Simplify.]
Step: 5
d ≈ 3.60
  [Find the positive square root.]
Step: 6
The distance between, A and B is 3.60 units.
Correct Answer is :   3.60 units
Q6Find the distance between A (-3, 6) and B (-4, 5) and round the solution to the nearest tenth.
A. 2.4 units
B. 3.4 units
C. 4.4 units
D. 1.4 units

Solutions
Share 
Step: 1
The distance between (x1, y1) and (x2, y2) = d = √[(x2 - x1)2 + (y2 - y1)2]
  [Use the distance formula.]
Step: 2
d = √[(-4 - (-3))2 + (5 - 6)2]
  [Replace (x1, y1) with (-3, 6) and (x2, y2) with (-4, 5).]
Step: 3
d = √[(-1)2 + (-1)2]
  [Subtract.]
Step: 4
d = √[1 + 1] = √2
  
Step: 5
d ≈ 1.414
  
Step: 6
The distance between A and B is 1.4 units.
  [Round the distance to the nearest tenth.]
Correct Answer is :   1.4 units
Q7Which of the following ordered pairs is at a distance of 5 units from (3, 4)?

A. (8, 4)
B. (9, 4)
C. (8, 5)
D. (10, 4)

Solutions
Share 
Step: 1
Distance d = √[(x2 - x1) 2 + (y2 - y1) 2]
  [Use the distance formula.]
Step: 2
Consider choice A, the distance between (3, 4) and (8, 4),
Step: 3
d = √[(8 - 3) 2 + (4 - 4) 2]
  [Replace (x1, y1) with (3, 4) and (x2, y2) with (8, 4).]
Step: 4
d = √(52 + 0)
  [Subtract.]
Step: 5
d = √25
  [Simplify.]
Step: 6
d = 5
  [Find the positive square root.]
Step: 7
Checking with the choices B, C and D, we find that those are not at a distance of 5 units from (3, 4).
Step: 8
thus the point (8, 4) is at a distance of 5 units from (3, 4).
Correct Answer is :   (8, 4)
Q8The coordinates of A are (2, 2). The first coordinate of B is 4 and the second coordinate is twice the second coordinate of A. Find the distance between A and B.

A. 5√2 units
B. 3√2 units
C. 2√2 units
D. 4√2 units

Solutions
Share 
Step: 1
The coordinates of A are (2, 2).
Step: 2
The first coordinate of B is 4 and the second coordinate is twice the second coordinate of A.
Step: 3
The second coordinate of B = 2 x second coordinate of A = 2 x 2 = 4
  [Substitute the second coordinate of A = 2.]
Step: 4
The coordinates of B are (4, 4)
Step: 5
Distance between the line-segment with endpoints (x1, y1) and (x2, y2) is √[(x2 - x1)2 + (y2 - y1)2]
Step: 6
Distance between A and B = √[(4 - 2)2 + (4 - 2)2]
  [Replace (x1, y1) with (2, 2) and (x2, y2) with (4, 4).]
Step: 7
= √(22 + 22)
  [Subtract.]
Step: 8
= √(4 + 4)
  [Evaluate powers.]
Step: 9
= √8
  
Step: 10
= 2√2
  [Simplify.]
Step: 11
The distance between A and B is 2√2 units.
Correct Answer is :   2√2 units
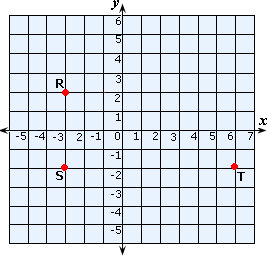
Q9The points R(- 3, 2), S(- 3, - 2) and T(6, - 2) represents the positions of Andrew, Roger and Peter respectively, playing in a playground. Find the distance between Andrew and Peter.


A. 9 units
B. 9.85 units
C. 10 units
D. 8.75 units

Solutions
Share 
Step: 1
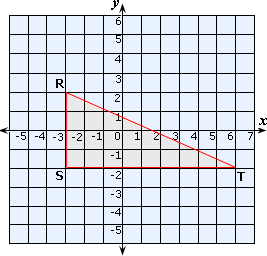
Plot the points R(- 3, 2), S(- 3, - 2) and T(6, - 2) in a Cartesian plane and join them.
Step: 2
Distance between the point R and the point S = 2 - (-2) = 4 units
  [Difference between the y-coordinates.]
Step: 3
Distance between the point S and the point T = 6 - (-3) = 9 units
  [Difference between the x-coordinates.]
Step: 4
Distance between Andrew and Peter = Distance between the point R and the point T
Step: 5
Since ΔRST is a right-angled triangle,
RT2 = RS2 + ST2
  [Pythagoras′ theorem.]
Step: 6
RT2 = 42 + 92
  [Substitute the values.]
Step: 7
RT2 = 16 + 81 = 97
  [Add.]
Step: 8
RT = 97 = 9.85 units
  [Take square root on both sides.]
Step: 9
Therefore, the distance between Andrew and Peter is 9.85 units.
Correct Answer is :   9.85 units
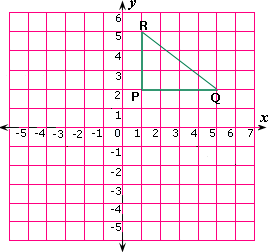
Q10The Cartesian plane shows the positions of Mary′s house P(1, 2), a library Q(5, 2) and a park R(1, 5). Find the distance between the park and the library.


A. 12 units
B. 25 units
C. 5 units
D. 10 units

Solutions
Share 
Step: 1
Distance between Mary′s house P and the park R = 5 - 2 = 3 units
  [Distance between the y-coordinates.]
Step: 2
Distance between Mary′s house P and the library Q = 5 - 1 = 4 units
  [Distance between the x-coordinates.]
Step: 3
The distance between the park R and the library Q = Length of RQ
Step: 4
Since ΔRPQ is a right-angled triangle,
RQ2 = PQ2 + PR2
  [Pythagoras′ theorem.]
Step: 5
RQ2 = 42 + 32
  [Substitute the values.]
Step: 6
RQ2 = 16 + 9 = 25
  [Add.]
Step: 7
RQ = 25 = 5 units
  [Take square root on both sides.]
Step: 8
Therefore, the distance between the park and the library is 5 units.
Correct Answer is :   5 units
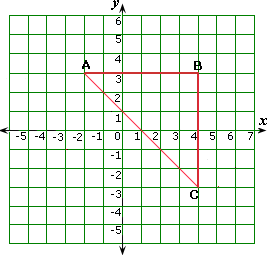
Q11Michael started from his house A(- 2, 3) and walked to the east to B(4, 3) and then towards the south to C(4, - 3). How far is he from his house now?


A. 7.45 units
B. 8.12 units
C. 8.49 units
D. 7.87 units

Solutions
Share 
Step: 1
Distance between the point A and the point B = 4 - (-2) = 4 + 2 = 6 units
  [Difference between the x-coordinates.]
Step: 2
Distance between the point B and the point C = 3 - (- 3) = 3 + 3 = 6 units
  [Difference between the y-coordinates.]
Step: 3
Distance between Michael′s house A and the point C = Length of AC
Step: 4
Since ΔABC is a right-angled triangle, AC2 = AB2 + BC2
  [Pythagoras′ theorem.]
Step: 5
AC2 = 62 + 62
  [Substitute the values.]
Step: 6
AC2 = 36 + 36 = 72
  [Add.]
Step: 7
AC = 72 = 8.49 units
  [Take square root on both sides.]
Step: 8
So, length of AC = 8.49 units
Step: 9
Therefore, Michael is at a distance of 8.49 units from his house now.
Correct Answer is :   8.49 units
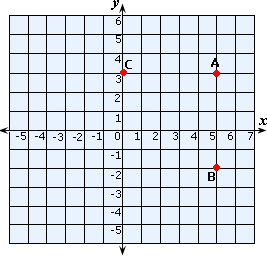
Q12The Cartesian plane shows the positions of three schools, A(5, 3), B(5, - 2) and C(0, 3), in a locality. How far is school B from school C?


A. 5.2 units
B. 7.07 units
C. 7 units
D. 50 units

Solutions
Share 
Step: 1
Plot the points A(5, 3), B(5, - 2) and C(0, 3) in a Cartesian plane and join them.
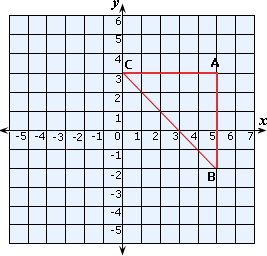
Step: 2
Distance between school A and C = 5 - 0 = 5 units
  [Difference between the x-coordinates.]
Step: 3
Distance between the school A and school B = 3 - (- 2) = 3 + 2 = 5 units
  [Difference between the y-coordinates.]
Step: 4
Since ΔBAC is a right-angled triangle,
BC2 = AB2 + AC2
  [Pythagoras′ theorem.]
Step: 5
BC2 = 52 + 52
  [Substitute the values.]
Step: 6
BC2 = 25 + 25 = 50
  [Add.]
Step: 7
BC = 50 = 7.07 units
  [Take square root on both sides.]
Step: 8
Therefore, school B is 7.07 units far from school C.
Correct Answer is :   7.07 units
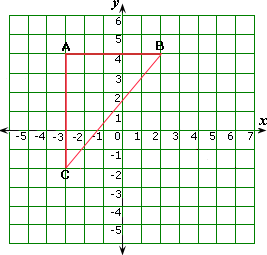
Q13Use Pythagorean theorem to find the length of BC¯.


A. 61 units
B. 67 units
C. 11 units
D. 61 units

Solutions
Share 
Step: 1
From the figure, AB = 2 - (- 3) = 2 + 3 = 5 units.
Step: 2
AC = 4 - (- 2) = 4 + 2 = 6 units.
Step: 3
From ΔABC, BC2 = AB2 + AC2
  [Apply Pythagorean theorem.]
Step: 4
BC2 = 52 + 62
  [Replace AB with 5 and AC with 6.]
Step: 5
BC2 = 25 + 36 = 61
  [Simplify.]
Step: 6
BC = 61
  [Take square root on both sides.]
Step: 7
The length of BC = 61 units.
Correct Answer is :   61 units

HighSchool Math