Solved Examples and Worksheet for Transformations-Translations
A. (
B. (
C. (
D. None of the above
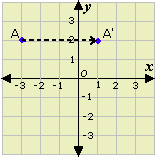
Step: 1
The x y x y
[The point P (x y
Step: 2
So, the rule for the translation is (x y x y
Correct Answer is : (x y x y
A. (
B. (
C. (
D. None of the above
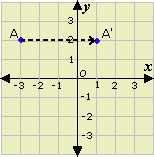
Step: 1
The x
Step: 2
So, the point P has been translated to the left.
Step: 3
Number of units, it has been translated left = 5 - (- 2) = 7 units
Step: 4
Step: 5
So, the point P has been translated up.
Step: 6
Number of units, it has been translated up = 9 - 5 = 4 units
Step: 7
So, the rule for the translation is (x y → x y
Correct Answer is : (x y → x y
A. Move 4 units left.
B. Move 2 units right.
C. Move 4 units right.
D. none of these
Step: 1
The coordinates before translation and after translation are (- 2, 3) and (2, 3).
Step: 2
The x y
Step: 3
Translation = 2 - (- 2) = 2 + 2 = 4 units right.
Step: 4
So, move 4 units right from (- 2, 3) to reach (2, 3).
Correct Answer is : Move 4 units right.
A. (0, -6) and (-4, -8)
B. (0, 6) and (-4, -8)
C. (0, 6) and (-4, 8)
D. None of the above
Step: 1
The coordinates of the line segment are (7, 6) and (3, -8).
Step: 2
The translation is done by 7 units left.
Step: 3
Since, the translation is done to left, the y
Step: 4
7 - 7 = 0 and 3 - 7 = -4.
[x
Step: 5
The new coordinates of the line segment are (0, 6) and (-4, -8).
Correct Answer is : (0, 6) and (-4, -8)
A. (3, - 8)
B. (2, 8)
C. (3, 8)
D. none of these
Step: 1
After the first translation, 2 units right and 5 units up, the x y
Step: 2
The coordinates after the first translation is (5, 9).
Step: 3
Again the image is translated, 2 units left and 1 unit down, the x y
Step: 4
The coordinates of the point after translation is (3, 8).
Correct Answer is : (3, 8)
A. Move 5 units left.
B. Move 5 units right.
C. Move 5 units up.
D. none of these
Step: 1
The two points are (4, 5) and (9, 5).
Step: 2
As the y x
Step: 3
The translation of the point is 9 - 4 = 5 units to the right.
Step: 4
So, to translate the point D(4, 5), to coordinates D′(9, 5), move 5 units right.
Correct Answer is : Move 5 units right.
A. (3, - 1)
B. (- 1, 3)
C. (- 1, 2)
D. (1, -3)
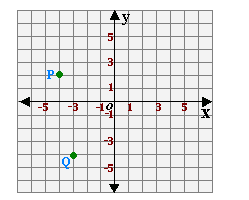
Step: 1
The point P is at (- 4, 2).
[From the coordinate plane.]
Step: 2
When the point is translated 3 units to the right the x y
Step: 3
After translation the x
[As the point is translated to the right.]
Step: 4
The new coordinates of the point P after translation is (- 1, 2)
Correct Answer is : (- 1, 2)
A. 10 units up
B. 10 units down
C. 10 units to the right
D. 10 units to the left
Step: 1
The horizontal change is the change in x
Step: 2
The horizontal change is 10.
Step: 3
Since the x x
Correct Answer is : 10 units to the left
A. (- 1, 4)
B. (4, 1)
C. (4, - 1)
D. (- 4, 1)
Step: 1
When (- 2, 2) is translated down 3 units, the y x
Step: 2
After translating (- 2, - 1) to 6 units right, the x y
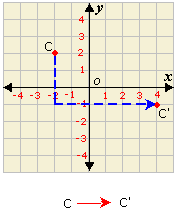

Step: 3
So, the coordinates of the new point C′ are (4, - 1).
Correct Answer is : (4, - 1)
A. (5, - 2)
B. (- 2, 0)
C. (- 2, 5)
D. (2, 0)
Step: 1
Plot the point O (0, 0).
Step: 2
Count down 2 units and right 5 units from the point O.
Step: 3
Graph O′.
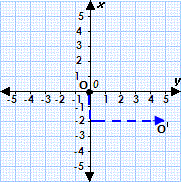

Step: 4
The coordinates of the image O′ are (5, - 2).
Correct Answer is : (5, - 2)
A. (
B. (
C. (
D. None of the above
Step: 1
The x
Step: 2
So, the point P has been translated to the left.
Step: 3
Number of units, it has been translated left = 8 - (- 3) = 11 units
Step: 4
The y
Step: 5
So, the point P has been translated up.
Step: 6
Number of units it has been translated up = 13 - 7 = 6 units
Step: 7
So, the rule for the translation is (x y → x y
Correct Answer is : (x y → x y
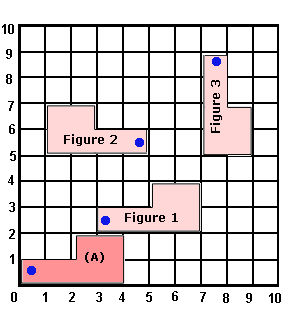
A. Figure 3
B. Figure 2
C. Figure 1
D. Figure 1 and Figure 2
Step: 1
A transformation in which every point of the figure moves the same distance and in the same direction is called translation or sliding.
Step: 2
Among the 3 figures, Figure 1 represents the slide of the figure(A).
[Figure 1 is 2 units up and 3 units to the right of figure (A).]
Correct Answer is : Figure 1
A. (- 5, 8)
B. (4, 8)
C. (8, 12)
D. (6, 10)
Step: 1
Plot the point B (3, 5).
Step: 2
Count 3 units right and 5 units up from the point B.
Step: 3
Graph the points.
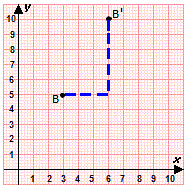

Step: 4
Therefore, the coordinates of the image of point B = (6, 10 )
Correct Answer is : (6, 10)
A. (5, -12)
B. (5, 12)
C. (4, 12)
D. None of the above
Step: 1
After the first translation, 3 units right and 7 units up, the x y
Step: 2
The coordinates after the first translation is (7, 13).
Step: 3
Again the image is translated 2 units left and 1 unit down, the x y
Step: 4
The coordinates of the point after translation is (5, 12).
Correct Answer is : (5, 12)
- Points, Rays, Angles, Lines and Line Segments-Geometry-Solved Examples
- Parallel Lines and Transversals-Geometry-Solved Examples
- Angle Sum Theorem and Medians in a Triangle-Geometry-Solved Examples
- Properties of Isosceles Triangles-Geometry-Solved Examples
- Proving Quadrilateral is a Parallelogram-Geometry-Solved Examples
- ASA and AAS Postulates -Triangle Congruence-Geometry-Solved Examples
- SSS and SAS Postulates-Triangle Congruence-Geometry-Solved Examples
- Transformations-Reflections-Geometry-Solved Examples
- Transformations-Rotations-Geometry-Solved Examples