Solved Examples and Worksheet for Proving Quadrilateral is a Parallelogram
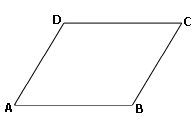
A. m
B. length of BC
C. length of CD
D. m
Step: 1
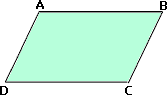
If one angle of the parallelogram is known, we can find all other angles and if length of one side is known, we can find the measure of opposite side since opposite sides of parallelogram are equal in measures.
Step: 2
Length of side AB = 3 in., therefore, CD = 3 in.
[Since AB and CD are opposite sides.]
Step: 3
We cannot find the length of the sides BC and AD.
Correct Answer is : length of BC
A. ABCD is not a parallelogram
B. ABCD is a kite
C. ABCD is a parallelogram
D. ABCD is a trapezoid
Step: 1
Mid point of diagonal AC ¯ 1 1 + 7 2 1 6 + 1 0 2
[Use mid point formula.]
Step: 2
Mid point of diagonal BD ¯ 4 + 1 4 2 1 7 + 9 2
[Use mid point formula.]
Step: 3
So, the diagonals of the quadrilateral bisect each other, and hence ABCD is a parallelogram.
Correct Answer is : ABCD is a parallelogram
A.
B.
C.
D.
Step: 1
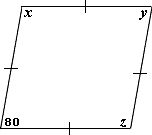
Since opposite angles of a parallelogram are congruent, we have y x z
Step: 2
Since adjacent angles of a parallelogram are supplementary, x y
Step: 3
[Substitute y
Step: 4
[Solve for x
Step: 5
So, z x
Correct Answer is : x y z
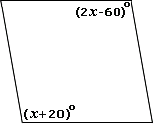
A.
B.
C.
D.
Step: 1
The opposite angles in a parallelogram are equal.
Step: 2
[∠ ∠
Step: 3
Let ∠ ∠ x
[∠ ∠
Step: 4
The sum of all the four angles in a parallelogram = 360°
Step: 5
Step: 6
83° + x x
[Substitute ∠ ∠ x
Step: 7
166° + 2x
[Combine like terms.]
Step: 8
2x
[Subtract 166° on both sides.]
Step: 9
2x
Step: 10
[Divide by 2 on both sides.]
Step: 11
Therefore, ∠ ∠ ∠
Correct Answer is : ∠ ∠ ∠
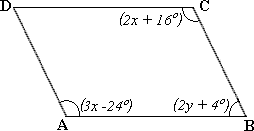
A.
B.
C.
D.
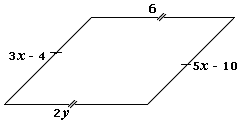
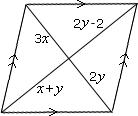
Step: 1
[Supplementary angles.]
Step: 2
3x y
Step: 3
3x y
[Simplify.]
Step: 4
[Supplementary angles.]
Step: 5
2y x
Step: 6
2x y
[Simplify.]
Step: 7
[Subtract (2) from (1).]
Step: 8
3(40) + 2y
[Substitute the value of x
Step: 9
2y ⇒ y
[Simplify.]
Step: 10
Hence the value of x y
Correct Answer is : x y
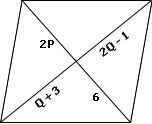
A.
B.
C.
D.
Step: 1
[Since, the diagonal bisects each other.]
Step: 2
[Simplify.]
Step: 3
3x y ⇒ y y
[Substitute the value of x
Step: 4
[Simplify.]
Step: 5
Step: 6
[Subtracting value of y
Step: 7
[Simplify.]
Correct Answer is : x y
- Points, Rays, Angles, Lines and Line Segments-Geometry-Solved Examples
- Parallel Lines and Transversals-Geometry-Solved Examples
- Angle Sum Theorem and Medians in a Triangle-Geometry-Solved Examples
- Properties of Isosceles Triangles-Geometry-Solved Examples
- ASA and AAS Postulates -Triangle Congruence-Geometry-Solved Examples
- SSS and SAS Postulates-Triangle Congruence-Geometry-Solved Examples
- Transformations-Reflections-Geometry-Solved Examples
- Transformations-Rotations-Geometry-Solved Examples
- Transformations-Translations-Geometry-Solved Examples
Related Worksheet
- Parallelogram Rule