Solved Examples and Worksheet for Transformations-Reflections
A. (3, - 6)
B. (3, 6)
C. (- 3, 6)
D. (- 3, - 6)
Step: 1
Reflection is the mirror image formed when the point is flipped over the line of reflection.
Step: 2
Plot the point K(- 3, 6).
Step: 3
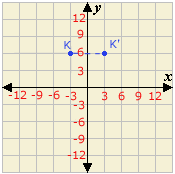
Step: 4
So, the coordinates of the image are K′(3, 6).
Correct Answer is : (3, 6)
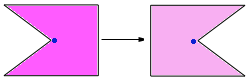
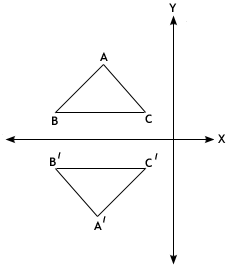
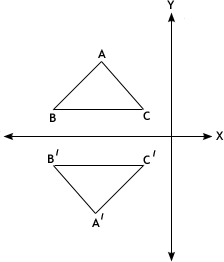
A. reflection
B. translation
C. rotation
D. rotation and reflection
Step: 1
A reflection flips a figure over a line of reflection. The reflected figure, or image, is the same as the original figure.
Step: 2
From the figure, it is clear that the figure is flipped over a line of reflection (the vertical line) and the reflected figure is the same as the original figure.
Step: 3
So, the transformation illustrated in the figure is reflection.
Correct Answer is : reflection
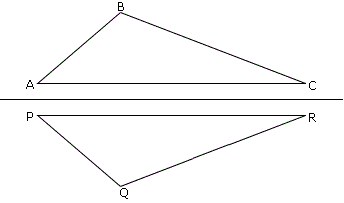
A.
B.
C.
D.
Step: 1
From the figure, PQ ¯ AB ¯ y ⇒ y
[Solve for y
Step: 2
From the figure, RQ ¯ CB ¯ x ⇒ x
[Solve for x
Correct Answer is : x y
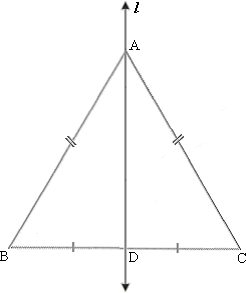
A. 2.3 cm2
B. 4.6 cm2
C. 5.3 cm2
D. 3.3 cm2
Step: 1
ΔABC is an equilateral triangle in which D is the mid point of BC ¯ AD ¯ BC ¯
Step: 2
Since medians are the perpendicular bisectors of the sides in an equilateral triangle, line l BC ¯
Step: 3
So, the reflection of ΔABD in line l
[Steps 1, 2.]
Step: 4
ΔABD and ΔADC are congruent
[Reflection is an isometry.]
Step: 5
So, area of ΔABD = area of ΔADC = 2.3 cm2
[Reflection does not change area.]
Correct Answer is : 2.3 cm2
A. (
B. (
C. (-
D. (-
Step: 1
Given point is (x y y y x y x y
Step: 2
So, the reflection image of P(x y y x y
Correct Answer is : (-x y
A. (- 2, - 2)
B. (2, 2)
C. (3, 2)
D. (2, - 2)
Step: 1
Since the triangle is reflected on the x x
Step: 2
Since A is 2 units up from the x x
Step: 3
The coordinates of point A′ are (-2 , -2)
Correct Answer is : (- 2, - 2)
A. (2, 4)
B. (- 2, - 4)
C. (3, 2)
D. None of the above
Step: 1
Since the triangle is reflected on the x x
Step: 2
Since A is 4 units up from the x x
Step: 3
The coordinates of point A′ are (-2, -4).
Correct Answer is : (- 2, - 4)
A. (4, 3)
B. (- 4, 3)
C. (4, - 3)
D. (3, - 4)
Step: 1
When a point is reflected over a horizontal line, the x y
Step: 2
The coordinates of the point after the reflection on x
Step: 3
When a point is reflected over a vertical line, the y x
Step: 4
The coordinate of the point when reflected over the y

Step: 5
The coordinates of the final image of point C' are (- 4, 3).
Correct Answer is : (- 4, 3)
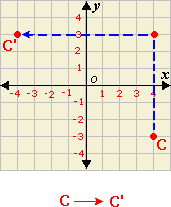
A. (5, 4)
B. (-5, 4)
C. (8, -4)
D. None of the above
Step: 1
When a point is reflected over a vertical line the y
Step: 2
The point P(-2, -4) is reflected over the line x
Step: 3
The distance of the point from the line x
Step: 4
So, the image of the point will be 5 units away from the line x
Step: 5
The x
Step: 6
So, the coordinates of the image of the point P(-2, -4) along x
Correct Answer is : (8, -4)
A. (5, 8)
B. (5, - 8)
C. (- 5, 8)
D. (- 5, - 8)
Step: 1
To find the image of any point P(a b x x y
Step: 2
So, the image of the point P(- 5, - 8) in x
Correct Answer is : (- 5, 8)
- Points, Rays, Angles, Lines and Line Segments-Geometry-Solved Examples
- Parallel Lines and Transversals-Geometry-Solved Examples
- Angle Sum Theorem and Medians in a Triangle-Geometry-Solved Examples
- Properties of Isosceles Triangles-Geometry-Solved Examples
- Proving Quadrilateral is a Parallelogram-Geometry-Solved Examples
- ASA and AAS Postulates -Triangle Congruence-Geometry-Solved Examples
- SSS and SAS Postulates-Triangle Congruence-Geometry-Solved Examples
- Transformations-Rotations-Geometry-Solved Examples
- Transformations-Translations-Geometry-Solved Examples
Related Worksheet
- Reflection