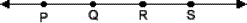Solved Examples and Worksheet for Points, Rays, Angles, Lines and Line Segments

Q1PQ is a line segment with a length of 20 units. R is a point on PQ such that PR is (34)th of PQ. Find the measures of PR and RQ.


A. 13 units and 7 units
B. 16 units and 4 units
C. 14 units and 6 units
D. 15 units and 5 units

Solutions
Share 
Step: 1
The length of PQ = 20 units.
Step: 2
PR = (34)(PQ)
  
Step: 3
PR = (34)(20) = 3 x 5 = 15
  
Step: 4
RQ = PQ - PR = 20 - 15 = 5
  [Substitute PQ = 20 and PR = 15]
Step: 5
PR = 15 units and RQ = 5 units.
Correct Answer is :   15 units and 5 units
Q2The points which do not lie on the same line are known as ______ points.

A. non-collinear
B. similar
C. collinear
D. congruent

Solutions
Share 
Step: 1
The points which do not lie on the same line are known as non-collinear points.
Correct Answer is :   non-collinear
Q3How many rays are there in the figure?


A. 8
B. 6
C. 10
D. 7

Solutions
Share 
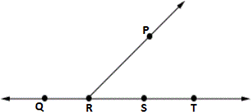
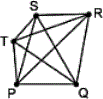
Step: 1
A ray is a part of a line. It has one end point and any number of points on one side of the end point.
Step: 2
A ray is named by the end point and any other point on the ray.
Step: 3
The rays in the figure, with Q as the end point are QP→, QR→ and QS→.
Step: 4
The rays in the figure, with P as the end point are PQ→ and PR→.
Step: 5
The rays in the figure, with R as the end point are RQ→ and RP→.
Step: 6
The rays in the figure, with S as the end point are SQ→ and ST→.
Step: 7
The ray in the figure, with T as the end point is TS→.
Step: 8
So, the total number of rays in the figure is 10.
  [3 + 2 + 2 + 2 + 1 = 10.]
Correct Answer is :   10
Q4How many lines can be drawn passing through a single point?

A. Three
B. Only one
C. Two
D. Infinite

Solutions
Share 
Step: 1
An infinite number of lines can be drawn through any given point.
Correct Answer is :   Infinite
Q5Identify the collinear points from the diagram?

A. A, C, D
B. A, B, C
C. B, C, D
D. A, B, C, D

Solutions
Share 
Step: 1
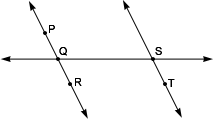
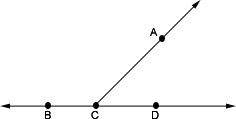
'If the points lie on the same line, then the points are called collinear points.'
Step: 2
From the figure, B, C and D lie on the same line.
Step: 3
So, B, C and D are the three collinear points.
Correct Answer is :   B, C, D
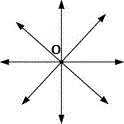
Q6How many line segments can be drawn using five non-collinear points?

A. 5
B. 10
C. infinite
D. 20

Solutions
Share 
Step: 1
Let P, Q, R, S and T be the five non-collinear points.
Step: 2
Join PQ¯, QR¯, RS¯, ST¯, TP¯, PR¯, PS¯, QT¯, QS¯ and RT¯ as shown in the figure.
Step: 3
So, the number of segments that can be drawn using five non-collinear points is 10.
Correct Answer is :   10
Q7How many line segments are there in the figure?

A. 5
B. 8
C. 3
D. 6

Solutions
Share 
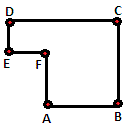
Step: 1
A line segment is a part of a line. It is made up of two points and all the points of the line that joins the two points.
Step: 2
In the figure, PQ¯, QR¯, RS¯, PR¯, QS¯ and PS¯ are the line segments.
Step: 3
So, the number of line segments in the figure is 6.
Correct Answer is :   6
Q8How many line segments can be drawn using six non-collinear points?
A. 36
B. 30
C. 15
D. 18

Solutions
Share 
Step: 1
Let A, B, C, D, E and F be the six non-collinear points.
Step: 2
Join AB¯, BC¯, CD¯, DE¯, EF¯, FA¯, AC¯, AD¯, AE¯, BD¯, BE¯, BF¯, CE¯, CF¯ and DF¯ as shown in the figure.
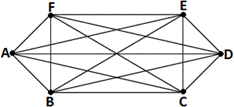
Step: 3
So, the number of segments that can be drawn using six non-collinear points is 15.
Correct Answer is :   15
Q9How many line segments are there in the figure?

A. 5
B. 7
C. 6
D. 8

Solutions
Share 
Step: 1
A line segment is a part of a line having exactly two end points.
Step: 2
The line segments in the figure are PR¯, QR¯, RS¯, ST¯, QS¯, RT¯, and QT¯.
  [Identify the parts of line with exactly two end points.]
Step: 3
So, there are 7 segments in the figure.
Correct Answer is :   7
Q10How many line segments are there in the figure shown?


A. 6
B. 5
C. 8
D. 7

Solutions
Share 
Step: 1
A line segment is a line or part of a line having exactly two end points.
Step: 2
The line segments in the figure are AB, BC, CD, DE, EF, and FA.
Step: 3
Therefore, there are 6 line segments in the given figure.
Correct Answer is :   6

HighSchool Math