SSS and SAS Postulates-Triangle Congruence-Geometry-Solved Examples

Solved Examples and Worksheet for SSS and SAS Postulates-Triangle Congruence

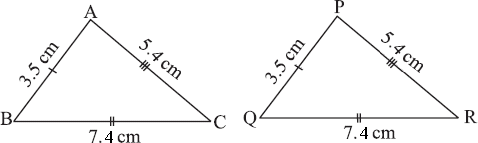
Q1In triangles ABC and PQR, AB = 3.5 cm, BC = 7.4 cm, AC = 5.4 cm, PQ = 3.5. cm, QR = 7.4 cm and PR = 5.4 cm. Examine whether the two triangles are congruent or not. If yes, what is the congruence rule and congruence relation in symbolic form ?

A. ΔABC ≅ ΔPQR (SSS Congruence Rule/Criterion)
B. ΔABC ≅ ΔPQR (SAS Congruence Rule/Criterion)
C. ΔABC ≅ ΔPQR (ASA Congruence Rule/Criterion)
D. ΔABC ≅ ΔPQR (RHS Congruence Rule/Criterion)

Solutions

Step: 1

: If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.

[SSS postulate.]

Step: 2

In the given triangles, three sides of first triangle are congruent to the corresponding three sides of second triangle.

Step: 3

So, ΔABC ≅ ΔPQR by the SSS congruence condition.

Correct Answer is : ΔABC ≅ ΔPQR (SSS Congruence Rule/Criterion)

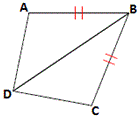
Q2What additional information is needed to prove that ΔADB ≅ ΔCDB by the SAS Postulate ?

A. ∠ABD = ∠CBD
B. AD¯ ≅ DC¯
C. ∠ABD = ∠CDB
D. ∠ADB = ∠CBD

Solutions

Step: 1

AB¯ ≅ CB¯

[Given.]

Step: 2

BD¯ ≅ BD¯

[Reflexive property of congruence.]

Step: 3

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.

[SAS Postulate.]

Step: 4

If ∠ABD = ∠CBD, then by the SAS Postulate, ΔADB ≅ ΔCDB.

Correct Answer is : ∠ABD = ∠CBD

Q3Which of the following can be applied directly to prove that ΔABC ≅ ΔEDC ?

A. SAS postulate
B. SSS postulate
C. ASA postulate
D. SAA postulate

Solutions

Step: 1

AC¯ ≅ CE¯

[Given.]

Step: 2

BC¯ ≅ CD¯

[Given.]

Step: 3

∠ACB = ∠EDC

[Vertical angles are congruent.]

Step: 4

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.

Step: 5

Thererfore, ΔABC ≅ ΔEDC by using SAS postulate.

Correct Answer is : SAS postulate

Q4Which of the following can be applied directly to prove that ΔABD ≅ ΔCBD ?

A. ASA postulate
B. SAA postulate
C. SSS postulate
D. SAS postulate

Solutions

Step: 1

AB¯ ≅ BC¯

[Given.]

Step: 2

AD¯ ≅ CD¯

[Given.]

Step: 3

BD¯ ≅ BD¯

[Reflexive property of congruence.]

Step: 4

If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.

Step: 5

Therefore, ΔABD ≅ ΔCBD by using SSS postulate.

Correct Answer is : SSS postulate

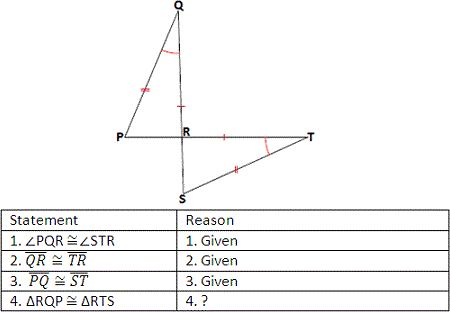
Q5Supply the reason to complete the proof below:

A. AAS postulate
B. SSS postulate
C. ASA postulate
D. SAS postulate

Solutions

Step: 1

If two sides and the included angle of one triangle are congruent to the two sides and the included angle of another triangle, then the two triangles are congruent.

Step: 2

As QR¯ ≅ TR¯, PQ¯ ≅ ST¯ and ∠PQR = ∠STR, by SAS theorem, we have ΔRQP ≅ ΔRTS.

Correct Answer is : SAS postulate

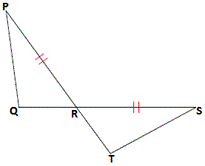
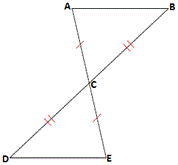
Q6What additional information is needed to prove that ΔQRP ≅ ΔTRS by the SAS Postulate ?

A. QR¯ ≅ ST¯
B. QR¯ ≅ TR¯
C. ∠PQR = ∠RTS
D. PQ¯ ≅ RS¯

Solutions

Step: 1

PR¯ ≅ SR¯

[Given.]

Step: 2

∠PRQ = ∠SRT

[Vertical angles congruent.]

Step: 3

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.

Step: 4

If QR¯ ≅ TR¯, then by the SAS Postulate, ΔQRP ≅ ΔTRS.

Correct Answer is : QR¯ ≅ TR¯

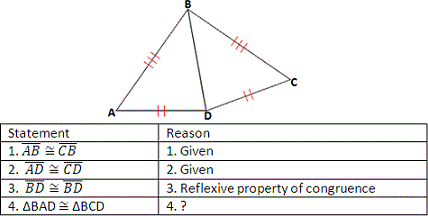
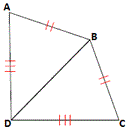
Q7Supply the reason to complete the proof below:

A. ASA postulate
B. SSS postulate
C. SAS postulate
D. AAS postulate

Solutions

Step: 1

If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.

[SSS Postulate.]

Step: 2

As AB¯ ≅ CB¯, AD¯ ≅ CD¯ and BD¯ ≅ BD¯, by SSS theorem, we have ΔBAD ≅ΔBCD.

Correct Answer is : SSS postulate

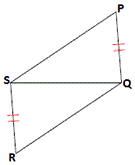
Q8What additional information is needed to prove that ΔPQS ≅ΔRSQ by the SSS Postulate ?

A. PS¯ ≅ QS¯
B. PQ¯ ≅ QR¯
C. ∠PQS = ∠RSQ
D. PS¯ ≅ QR¯

Solutions

Step: 1

PQ¯ ≅ RS¯

[Given.]

Step: 2

QS¯ ≅ QS¯

[Reflexive property of congruence.]

Step: 3

If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.

[SSS Postulate.]

Step: 4

If PS¯ ≅ RQ¯, then by the SSS postulate, ΔPQS ≅ΔRSQ.

Correct Answer is : PS¯ ≅ QR¯

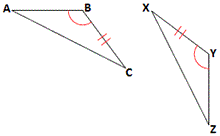
Q9What additional information is needed to prove that ΔABC ≅ ΔZYX by the SAS Postulate ?

A. AB¯ ≅ XZ¯
B. ∠CAB = ∠XZY
C. AB¯ ≅ ZY¯
D. AC¯ ≅ XZ¯

Solutions

Step: 1

BC¯ ≅ YX¯

[Given.]

Step: 2

∠ABC = ∠ZYX

[Given.]

Step: 3

If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.

Step: 4

If AB¯ ≅ ZY¯, then by the SAS Postulate, ΔABC ≅ ΔZYX.

Correct Answer is : AB¯ ≅ ZY¯

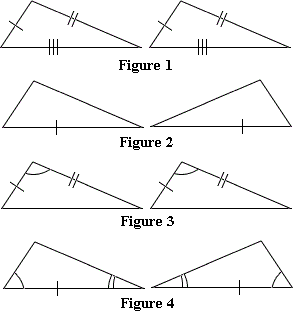
Q10Which of the following pair of triangles are congruent by the SAS congruence condition?

A. Figure 1
B. Figure 4
C. Figure 3
D. Figure 2

Solutions

Step: 1

If two sides and the included angle in one triangle are congruent to two sides and the included angle in another triangle, then the two triangles are congruent

[SAS postulate.]

Step: 2

In Figure 3, two sides and the included angle of first triangle are congruent to the corresponding two sides and the included angle of second triangle.

Step: 3

So, the pair of triangles in Figure 3 are congruent by the SAS congruence condition.

Correct Answer is : Figure 3

Solved Examples and Worksheet for SSS and SAS Postulates-Triangle Congruence

Related Worksheet

Related Topic

HighSchool Math