Solved Examples and Worksheet for Solving Problems Using Rate of Change

Q1The table shows the number of girls admitted in a school in two consecutive years. Assuming the same rate of change for the students admitted in subsequent years, estimate the number of girls admitted in the year 2003.
YearNumber of girls
19982400
19993000

A. 4800
B. 5400
C. 6000
D. 4200

Solutions
Share 
Step: 1
Average rate of change = Change in the number of girls admitted in schoolChange in time
Step: 2
= 3000-24001999-1998
Step: 3
= 600 per year
Step: 4
So, the number of girls admitted in the year 2003 is 2400 + 5(600) = 5400
Correct Answer is :   5400
Q2The annual income of Jeff in 1996 was $30,000. His income rose to $36,000 in 1998. At this rate what would be the annual income of Jeff in 2004?

A. $42,000
B. $54,000
C. $60,000
D. $57,000

Solutions
Share 
Step: 1
Average rate of change = Change in the annual incomeChange in time
Step: 2
= 36000-300001998-1996
Step: 3
= 60002 = $3000 per year
Step: 4
So, the annual income of Jeff in the year 2004 is $(30,000 + 8(3,000)) = $54,000
Correct Answer is :   $54,000
Q3A telephone service charges $10 per month plus 15 cents per minute. The table shows the relationship between the number of minutes and the cost. Use the rate of change to identify a linear equation for the data shown in the table.
Number of Minutes (x)1020304050
Cost in Dollars (y)11.501314.501617.50


A. y = 0.15x + 10
B. x = 0.15y + 10
C. y = 0.15x - 10
D. x = 0.15y - 10

Solutions
Share 
Step: 1
Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.
Step: 2
The input variable x is the number of minutes and the output variable y gives the total cost.
Step: 3
Change in output values = 1.50.
Step: 4
Change in input values =10.
Step: 5
Rate of change= Change in output valuesChange in input values = 1.5010 = 0.15
Step: 6
Working backwards with the values in the table, we get (0, 10).
Step: 7
So, the linear equation that satisfies the table is y = 0.15x+10.
  [Substitute rate of change and y - intercept values.]
Correct Answer is :   y = 0.15x + 10
Q4A water tank contains 30 litres of water. A pipe fills the tank with 10 litres of water every half an hour. The table shows the relationship between the number of minutes and water level in the tank. Use the rate of change to identify a linear equation for the data shown in the table.
Number of Minutes (x)306090120150
Water Level (y)4050607080


A. y = 13x - 30
B. x = 13y - 30
C. x = 13y + 30
D. y = 13x + 30

Solutions
Share 
Q5Holly earns $70 everyday by working for 7 hours. She gets $20 for every extra hour worked. The table shows the relationship between the number of extra hours and Holly's total earnings per day. Use the rate of change to identify a linear equation for the data shown in the table.
Number of Extra Hours (x)123
Total Earnings (y)90110130

A. x = 20y + 70
B. y = 20x - 70
C. y = 20x + 70
D. x = 20y - 70

Solutions
Share 
Step: 1
Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.
Step: 2
The input variable x is the number of extra hours and the output variable y gives the total earnings of John per day.
Step: 3
Change in output values = 20
Step: 4
Change in input values = 1
Step: 5
Rate of change = chnage in output valueschange in input values = 201 = 20
Step: 6
Working backwards with the values in the table, we get (0, 70).
Step: 7
So, the linear equation that satisfies the table is y = 20x + 70.
  [Substitute rate of change and y - intercept values.]
Correct Answer is :   y = 20x + 70
Q6A company spends $100 per month on its workers plus 7% commission on its sales.The table shows the relationship between the sales and expenditure of the company. Use the rate of change to identify a linear equation for the data shown in the table.
Sales Worth (x)100200300400
Expenditure in Dollars (y)107114121128


A. x = 0.07y + 100
B. y = 0.07x - 100
C. x = 0.07y - 100
D. y = 0.07x + 100

Solutions
Share 
Step: 1
Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.
Step: 2
The input variable x is the sales worth and the output variable y is the expenditure.
Step: 3
Change in output values = 7
Step: 4
Change in input values = 100
Step: 5
Rate of change = change in output valueschange in input values = 7100 = 0.07
Step: 6
Working backwards with the values in the table, we get (0, 100).
Step: 7
So, the linear equation that satisfies the table is y = 0.07x + 100.
  [Substitute rate of change and y - intercept values.]
Correct Answer is :   y = 0.07x + 100
Q7The graph shows the relationship between Sam′s wages and the number of hours he worked. Interpret the meaning of the slope as a rate of change.


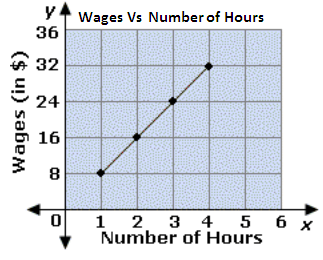
A. Sam earns $7 per hour.
B. Sam earns $8 per hour.
C. Sam earns $9 per hour.
D. Sam earns $6 per hour.

Solutions
Share 
Step: 1
The slope of the line = riserun = $hour =y2-y1x2-x1 = 32 - 244 - 3 , where any of the points on the line could be selected.
Step: 2
32 - 244 - 3 = 81 = 8
Step: 3
Since the slope of the line is 8, Sam earns $8 per hour.
Correct Answer is :   Sam earns $8 per hour.
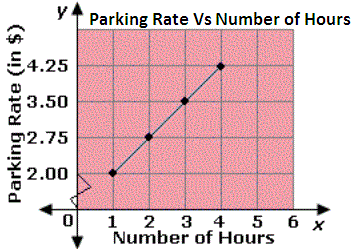
Q8The graph shows the relationship between parking rate and the number of hours. Interpret the meaning of the slope as a rate of change.


A. Parking rate for every additional hour increases by $2.
B. Parking rate for every additional hour increases by $0.75.
C. Parking rate for every vehicle increases by $0.75.
D. Parking rate for every additional hour decreases by $2.

Solutions
Share 
Step: 1
The slope of the line = riserun = $hour= y2-y1x2-x1= 4.25 - 3.504 - 3 , where any of the points on the line could be selected.
Step: 2
4.25 -3.504 - 3 = 0.751 = 0.75
Step: 3
Since the slope of the line is 0.75, the parking rate increases $0.75 per hour.
Correct Answer is :    Parking rate for every additional hour increases by $0.75.
Q9From 1985 to 1997, the number of schools in a state is increased by about 150 per year. In 1985, there were 1000 schools. Find the number of schools in the year 1991.

A. 1050
B. 12000
C. 3050
D. 1900

Solutions
Share 
Step: 1
The rate of increase is 150 per year.
Step: 2
Let t = 0 represent the year 1985.
Step: 3
The year 1991 is represented by t = 6.
Step: 4
This situation is represented by the linear equation y = 150t + 1000.
Step: 5
At t = 6, y = 150(6) + 1000 = 900 + 1000 = 1900
Step: 6
So, the number of schools in the year 1991 is 1900.
Correct Answer is :   1900
Q10Find the value of y when x = 4.46 using the relation between x and y given in the following data.
Input- 1.200.61.52.43.33.6
Output5.243.42.51.60.70.4

A. - 0.46
B. 8.46
C. 0.46
D. - 8.46

Solutions
Share 
Step: 1
Rate of change = change in output valueschange in input values
Step: 2
InputOutputChange in input valuesChange in output valuesRate of change
- 1.25.2
041.2 -1.2- 1
0.63.40.6- 0.6- 1
1.52.50.9- 0.9- 1
2.41.60.9- 0.9- 1
3.3 0.70.9-0.9- 1
3.6 0.40.3- 0.3- 1
Step: 3
The rate of change = - 1
Step: 4
The linear equation that represents the data is y = 4 + (- 1) x.
Step: 5
y = 4 - x
Step: 6
When x = 4.46, y = - 0.46
Correct Answer is :   - 0.46
Q11The following table shows Joseph's earnings for the number of extra cell phones he sold. How many extra cell phones did he sell, if he earned $96?
Cell phones123
Earnings728088


A. 14
B. 5
C. 4
D. 3

Solutions
Share 
Step: 1
Rate of change = 80 - 722 - 1 = 8
Step: 2
This situation can be modeled by the linear equation y = 8t + 64
Step: 3
96 = 8t + 64 gives t = 4
Step: 4
Joseph needs to sell 4 cell phones.
Correct Answer is :   4
Q12The table shows the weight of a baby for different months. Find the rate of change in weight?
Months24273033
Weight (pounds)30313233


A. 9 pounds per year
B. 4 pounds per year
C. 3 pounds per year
D. 13 pounds per year

Solutions
Share 
Step: 1
Rate of change = Change in weightChange in time
Step: 2
= 31-3027-24 = 13 pounds per month
Step: 3
So, the rate of change in weight of a child is 13 × 12 = 4 pounds per year.
Correct Answer is :   4 pounds per year

HighSchool Math