Solved Examples and Worksheet for Representing Exponential Functions Using Tables or Graphs
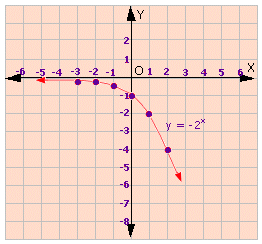
A. Domain is set of all positive numbers and the range is set of all real numbers.
B. Domain is set of all negative numbers and the range is set of all negative numbers.
C. Domain is set of all real numbers and the range is set of all positive numbers.
D. Domain is set of all real numbers and the range is set of all negative numbers.
Step: 1
From the graph of the function, y x x y
Step: 2
The domain of y x
Correct Answer is : Domain is set of all real numbers and the range is set of all negative numbers.
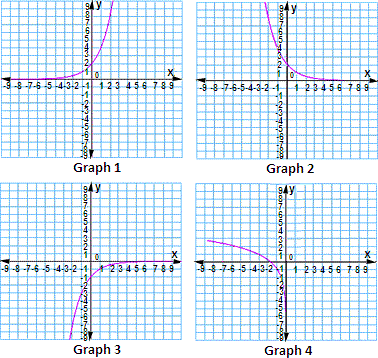
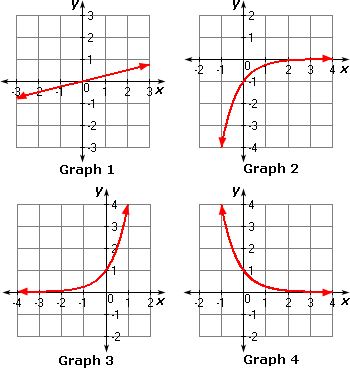
A. Graph 4
B. Graph2
C. Graph 3
D. Graph 1
Step: 1
Make a table of values that includes both positive and negative x
Step: 2
[Original exponential function.]
Step: 3
Substitute the values - 2, - 1, 0, 1, 2 and 3 for x y ( 2 ) x
Step: 4
[Replace x
Step: 5
= 2(1 4
[Use definition of negative exponent.]
Step: 6
[Replace x
Step: 7
= 2(1 2
[Use definition of negative exponent.]
Step: 8
[Replace x
Step: 9
= 2 × 1 = 2
[20 = 1.]
Step: 10
[Replace x
Step: 11
[Replace x
Step: 12
[Replace x
Step: 13

Step: 14
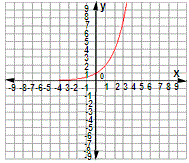
Draw a coordinate plane and plot the six points given by the table. Then draw a smooth curve through the points.

Step: 15
So, the graph of the exponential function y ( 2 ) x
Correct Answer is : Graph 1
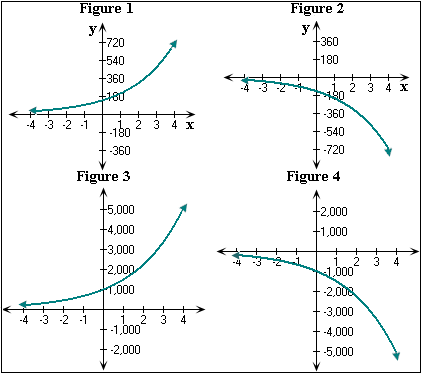
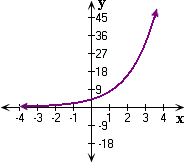
A. Figure 1
B. Figure 3
C. Figure 4
D. Figure 2
Step: 1
Draw a table for the number of viewers of a sports channel in 1996, 1997, 1998, 1999, 2000, 2001, 2002. x
| - 2 | - 1 | 0 | 1 | 2 | 3 | 4 | |
| 62.2 | 93.3 | 140 | 210 | 315 | 472.5 | 708.8 |
Step: 2
Draw a coordinate plane and plot the points given by table. Then draw a smooth curve through the points.
Step: 3
Notice that the graph has y x x
Step: 4
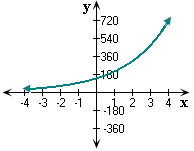
Step: 5
So, the graph of the number of viewers of the sports channel y = 140(1.5)x matches with the Figure 1.
Correct Answer is : Figure 1
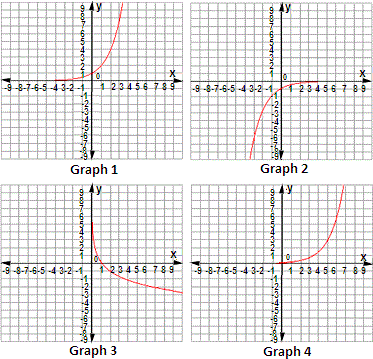
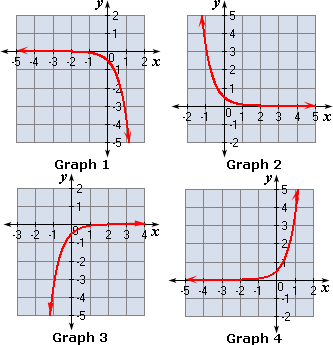
A. Graph 4
B. Graph 2
C. Graph 1
D. Graph 3
Step: 1
Make a table of values that includes both positive and negative x
Step: 2
[Original exponential function.]
Step: 3
Substitute the values - 2, - 1, 0, 1, 2 and 3 for x y 1 2 - x
Step: 4
[Replace x
Step: 5
= 1 4
Step: 6
[Replace x
Step: 7
= 1 2
Step: 8
[Replace x
Step: 9
= 1
[(1 2
Step: 10
[Replace x
Step: 11
= 1 ( 1 2 )
[Use definition of negative exponent.]
Step: 12
[Replace x
Step: 13
[Replace x
Step: 14
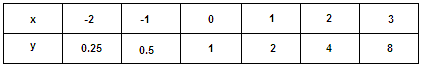
Step: 15
Draw a coordinate plane and plot the six points given by the table. Then draw a smooth curve through the points.

Step: 16
So, the graph 1 matches with given exponential function.
Correct Answer is : Graph 1
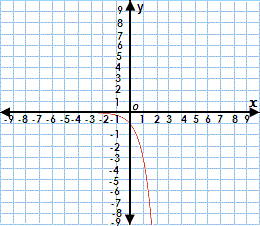
A. The domain is all positive real numbers and the range is all real numbers.
B. The domain is all real numbers and the range is all positive real numbers.
C. The domain is all real numbers and the range is all negative real numbers.
D. The domain is all negative real numbers and the range is all negative real numbers.
Step: 1
From the graph of the function, y x x y
Step: 2
The domain of y x
Correct Answer is : The domain is all real numbers and the range is all negative real numbers.
A. Positive
B. Positive
C. Negative
D. Negative
Step: 1
Make the table of values for the equation y x
| - 3 | - 2 | - 1 | 0 | 1 | 2 | |
| 2 | 6 | 18 | 54 |
Step: 2
Draw a coordinate plane and plot the six points given by the table.
Step: 3
Draw a smooth curve through the plotted points.
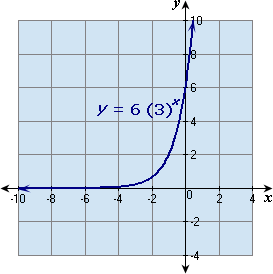

Step: 4
The graph gets closer to the negative side of the x x
Correct Answer is : Negative x
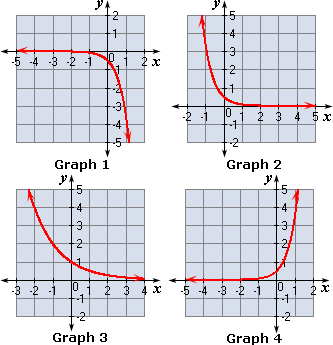
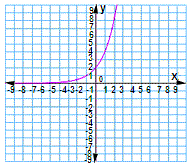
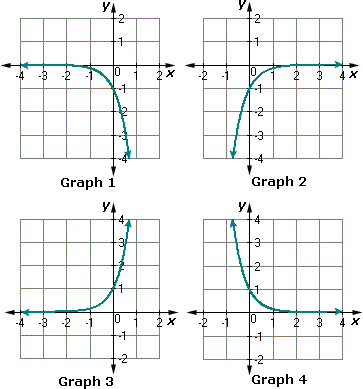
A. Graph 2
B. Graph 3
C. Graph 4
D. Graph 1
Step: 1
[Original function.]
Step: 2
Take some values for x
Step: 3
[Substitute - 3 for x
Step: 4
= - 0.001
[Simplify.]
Step: 5
[Substitute - 2 for x
Step: 6
= - 0.01
[Simplify.]
Step: 7
[Substitute - 1 for x
Step: 8
= - 0.07
[Simplify.]
Step: 9
[Substitute 0 for x
Step: 10
= - 0.5
[Simplify.]
Step: 11
[Substitute 1 for x
Step: 12
= - 3.5
[Simplify.]
Step: 13
Plot these values in a graph.
Step: 14
Among the graphs, Graph 1 represents the exponential function f x 1 2 x
Correct Answer is : Graph 1
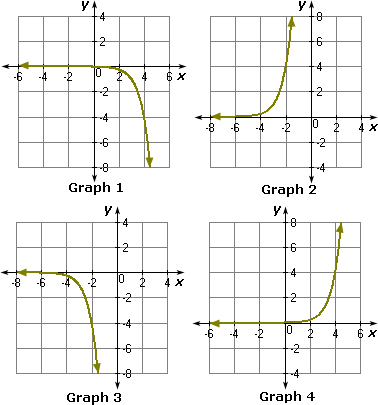
A. Graph 2
B. Graph 4
C. Graph 1
D. Graph 3
Step: 1
Make a table of values that includes both positive and negative x
| - 1 | 0 | 1 | 2 | 3 | 4 | |
| 0.004 | 0.016 | 0.0625 | 0.25 | 1 | 4 |
Step: 2
Graph the ordered pairs in the table shown and connect the points with a smooth curve.
Step: 3
Then the graph obtained is as shown in Graph 4.
Step: 4
So, Graph 4 represents the equation y x
Correct Answer is : Graph 4
A. Graph 1
B. Graph 2
C. Graph 4
D. Graph 3
Step: 1
Make a table of values that includes both positive and negative x
| - 1 | 0 | 1 | 2 | 3 | |
| - 4 | - 1 | - 0.25 | - 0.0625 | - 0.016 |
Step: 2
Graph the ordered pairs in the table shown and connect the points with a smooth curve.
Step: 3
Then the graph obtained matches with Graph 2.
Step: 4
So, Graph 2 represents the equation y 1 4 x
Correct Answer is : Graph 2
A. Graph 2
B. Graph 3
C. Graph 1
D. Graph 4
Step: 1
[Original function.]
Step: 2
Take some values for x
Step: 3
[Substitute - 3 for x
Step: 4
= 171.5
[Simplify.]
Step: 5
[Substitute - 2 for x
Step: 6
= 24.5
[Simplify.]
Step: 7
[Substitute - 1 for x
Step: 8
= 3.5
[Simplify.]
Step: 9
[Substitute 0 for x
Step: 10
= 0.5
[Simplify.]
Step: 11
[Substitute 1 for x
Step: 12
= 0.07
[Simplify.]
Step: 13
Plot these values in a graph.
Step: 14
Among the graphs, Graph 2 represents the exponential function f x 1 2 x
Correct Answer is : Graph 2
A. domain is all real numbers and the range is all positive real numbers.
B. domain is all negative numbers and the range is all negative real numbers.
C. domain is all real numbers and the range is all real numbers.
D. domain is all positive real numbers and the range is all real numbers.
Step: 1
The graph of the function, y ( 2 ) x x y
Step: 2
So, the domain of y ( 2 ) x
Correct Answer is : domain is all real numbers and the range is all positive real numbers.
A. Graph 1
B. Graph 2
C. Graph 4
D. Graph 3
Step: 1
Make a table of values that includes both positive and negative x
| - 3 | - 2 | - 1 | 0 | |
| 0.003 | 0.02 | 0.143 | 1 |
Step: 2
Graph the ordered pairs in the table shown and connect the points with a smooth curve.
Step: 3
Then the graph obtained matches with Graph 3.
Step: 4
So, Graph 3 represents the equation y x
Correct Answer is : Graph 3
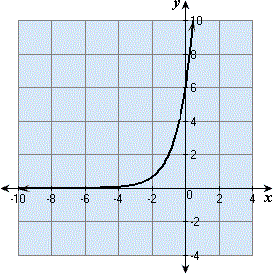
A.
B.
C.
D.
Step: 1
Let the exponential equation be y y r x
Step: 2
6 = y r y
[From the graph, substitute the point (0,6) in the general equation]
Step: 3
( 1 + r 2 y 0
Step: 4
= y r
[From the graph,substitute the point ( - 1,2) in the general equation]
Step: 5
(1 + r 2 6
[ From step 2, y
Step: 6
1 + r
[Simplify]
Step: 7
Therefore, the equation is y x
[Step 1, 2 and 5]
Correct Answer is : y x
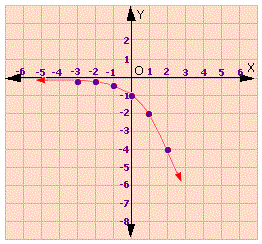
A.
B.
C.
D.
Step: 1
Let the exponential equation be y y r x
Step: 2
- 1 = y r y
[ From the graph, substitute the point ( 0 , -1 ) in the general equation]
Step: 3
- 2 = y r
[From the graph, substitute the point ( 1,- 2 ) in the general equation]
Step: 4
(1 + r - 2 y 0
Step: 5
(1 + r - 2 - 1
[From step 2, y
Step: 6
1 + r
[Simplify]
Step: 7
Therefore , the equation is y x
[Step 1,2 and 5]
Correct Answer is : y x
- Determining Whether a given Relation is a Function-Gr 8-Solved Examples
- Classifying Relations as Linear or Nonlinear-Gr 8-Solved Examples
- Identifying Functions-Gr 8-Solved Examples
- Graphing Linear Functions for a Given Domain-Gr 8-Solved Examples
- Graphing Linear Functions based on an x/y Table-Gr 8-Solved Examples
- Graphing Linear Equations-Gr 8-Solved Examples
- Finding the Rule of a Function Table-Gr 8-Solved Examples
- Solving Problems Using Rate of Change-Gr 8-Solved Examples
Related Worksheet
- Exponential Function