Determining Whether a given Relation is a Function-Gr 8-Solved Examples

Solved Examples and Worksheet for Determining Whether a given Relation is a Function

Q1Determine whether the relation represented by the set of ordered pairs is a function. Give the domain and range, if it is a function.
(- 3, - 3), (- 3, - 4), (2, 5), (3, 6).

A. It is not a function
B. It is a function, domain: - 3, 4 and 6, range: - 3, - 4, 5 and 6
C. It is a function, domain: - 3, 2 and 3, range: - 3, - 4, 5 and 6
D. It is a function, domain: - 3, 2 and 3, range: 2, - 3, - 4, 5 and 6

Step: 1

A relation is a function if every input has exactly one output.

Step: 2

The relation is not a function because the input - 3 has two outputs: - 3 and - 4.

Correct Answer is : It is not a function

Q2Determine whether the relation represented by the set of ordered pairs below is a function. Give the domain and range, if it is a function.
(27, - 29), (27, - 30), (28, - 31), (29, - 32).
A. It is a function and the domain is 27, 28 and 29, range: - 29, - 30, - 31 and - 32
B. It is a function and the domain is 27, 28 and 29, range: 28, - 29, - 30, - 31 and - 32
C. It is not a function
D. It is a function and the domain is 27, 30 and 32, range: - 29, - 30, - 31 and - 32

Step: 1

A relation is a function, if, every input, has exactly one output.

Step: 2

The relation is not a function because the input 27 has two outputs: - 29 and - 30.

Correct Answer is : It is not a function

Q3Choose the formula which is not a function.
A. x = 2 + y
B. y = x + 5
C. y = x²
D. x = 2 y²

Step: 1

For the choice A: x = 2 + y ⇒ y = x - 2
The graph has unique y value for a unique value of x. Hence, it is a function. In other words, no vertical line intersects the graph in more than one point.

[Vertical line test.]

Step: 2

For the choice B: y = x + 5
The graph has unique y value for a unique value of x. Hence, it is a function. In other words, no vertical line intersects the graph in more than one point.

[Vertical line test.]

Step: 3

For the choice C: y = x²
Here, the graph has two y values for every positive value of x. Hence, it is a function. In other words, no vertical line intersects the graph in more than one point.

[Vertical line test.]

Step: 4

For the choice D: x = 2y² ⇒ y = ± x2
Here, the graph has two x values for every positive value of y. Hence, it is not a function. In other words, the vertical line intersects the graph in more than one point.

[Vertical line test.]

Correct Answer is : x = 2 y²

Q4Draw the mapping diagram for the relation and determine whether it is a function or not.
{(5, 3), (6, - 3), (- 6, 2)}

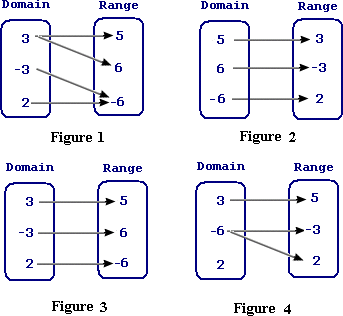
A. Figure 3, Relation is not a function
B. Figure 4, Relation is a function
C. Figure 1, Relation is not a function
D. Figure 2, Relation is a function

Step: 1

Draw the mapping diagram for the given relation.

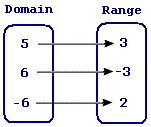
Step: 2

A relation is a function if each element in the domain is paired with one and only one element in the range.

Step: 3

From the mapping diagram, it can be observed that figuire 2 matches with the given relation and it also represents that given relation is a function.

Correct Answer is : Figure 2, Relation is a function

Q5Determine whether the relation represented by the set of ordered pairs below is a function. Give the domain and range, if it is a function.
(2, - 4), (2, 5), (2, - 6), (4, 7).
A. It is a function, domain: 2 and 4, range: 3, - 4, 5, - 6 and 7
B. It is not a function
C. It is a function, domain: 2, 5 and 7, range: - 4, 5, - 6 and 7
D. It is a function, domain: 2 and 4, range: - 4, 5, - 6 and 7

Step: 1

A relation is a function if every input has exactly one output.

Step: 2

The relation is not a function because the input 2 has three outputs: - 4, 5 and - 6.

Correct Answer is : It is not a function

Q6Determine whether the relation is a function. If so, find its domain and range.
(1, - 2), (2, - 2), (- 4, - 2), (1, 3)

A. It is a function, domain: 1, 4, - 2, and 1, range: - 2.
B. It is a function, domain: 1, 4, - 2, and 1, range: - 2 and 3.
C. It is not a function.
D. It is a function, domain: - 1, 2, - 4, and 1, range: - 2 and 3.
E. It is a function, domain: - 2 and 3, range: - 1, 2, - 4, and 1.

Step: 1

A relation is a function if for every input there is exactly one output.

Step: 2

The relation given is not a function because the input 1 has two outputs - 2 and 3.

Correct Answer is : It is not a function.

Q7Determine whether the relation represented by the set of ordered pairs is a function. Identify the domain and range, if it is a function.
(5, 14), (6, 16), (7, 18), (8, 20)

A. it is not a function
B. it is a function
domain: {6, 7, 8} range: {16, 18, 20}
C. it is a function
domain: {5, 6, 7, 8} range: {14, 16, 18, 20}
D. it is a function
domain: {5, 6, 7} range: {14, 16, 18}

Step: 1

A relation is a function if every input has exactly one output.

Step: 2

The given relation has exactly one output for each input. So, the relation is a function.

Step: 3

The domain is {5, 6, 7, 8} and range is {14, 16, 18, 20}.

Correct Answer is : it is a function
domain: {5, 6, 7, 8} range: {14, 16, 18, 20}

Q8Determine whether the relation represented by the set of ordered pairs below is a function. Give the domain and range, if it is a function.
(18, - 20), (18, - 21), (19, - 22), (20, - 23).

A. It is a function and the domain is 18, 19 and 20; range: 19, - 20, - 21, - 22 and - 23
B. It is a function and the domain is 18, 19 and 20; range: - 20, - 21, - 22 and - 23
C. It is a function and the domain is 18, 21 and 23; range: - 20, - 21, - 22 and - 23
D. It is not a function

Step: 1

A relation is a function, if, every input, has exactly one output.

Step: 2

The relation is not a function because the input 18 has two outputs: - 20 and - 21.

Correct Answer is : It is not a function

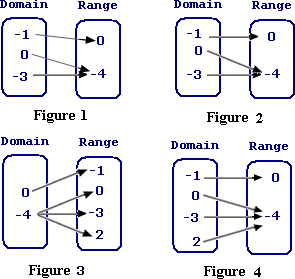
Q9Draw the mapping diagram for the relation and determine whether it is a function or not.
{(- 1, 0), (0, - 4), (- 3, - 4), (2, - 4)}

A. Figure 1, Relation is not a function
B. Figure 4, Relation is a function
C. Figure 2, Relation is a function
D. Figure 3, Relation is not a function

Step: 1

Draw the mapping diagram for the given relation.

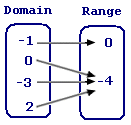
Step: 2

A relation is a function if each element in the domain is paired with one and only one element in the range.

Step: 3

From the mapping diagram, it can be observed that the given relation is a function.

Correct Answer is : Figure 4, Relation is a function

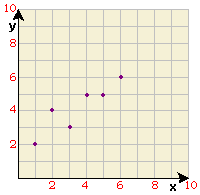
Q10Determine whether the relation represented in the graph is a function or not.

A. It is a function, domain: 2, 3, 4, 5 and 6; range: 1, 2, 3, 4, 5 and 6.
B. It is not a function.
C. cannot be determined
D. It is a function.

Step: 1

A relation is a function if every input has exactly one output.

Step: 2

In the plot, for each x-coordinate, there is only one y-coordinate.

[No two points have same y-coordinates.]

Step: 3

So, the relation is a function.

Correct Answer is : It is a function.

Q11A relation is observed between the number of days of preparation by a student for math, science and statistics tests and the points he scored. The relation is: {(4, 66), (5, 96), (3, 50)}. Determine if this relation is a function or not.

A. cannot be determined
B. It is a function with same domain and range.
C. It is not a function.
D. It is a function.

Step: 1

The given ordered pairs are: {(4, 66), (5, 96), (3, 50)}

Step: 2

A relation is a function if each input corresponds to one and only one output.

Step: 3

So, the given relation is a function.

Correct Answer is : It is a function.

Q12Determine whether the relation is a function or not. If so, find its domain and range.
{(2, - 3), (3, - 3), (- 4, - 3), (2, 1)}

A. It is not a function.
B. It is a function, domain: - 3 and 1, range: - 2, 3, - 4, and 2.
C. It is a function, domain: - 2, 3, - 4, and 2, range: - 3 and 1.
D. It is a function, domain: 2, 4, - 3, and 2, range: - 3 and 1.

Step: 1

A relation is a function if for every input there is exactly one output.

Step: 2

The relation given is not a function because the input 2 has two outputs - 3 and 1.

Correct Answer is : It is not a function.

Q13Determine whether the relation is a function or not. Identify the domain and range, if it is a function.

Input	Output
- 3	- 5
- 4	- 7
- 9	- 19
- 6	- 11

A. It is a function, domain: - 5, - 7, - 19 and - 11, range: - 3, - 4, - 9 and - 6.
B. It is a function, domain: - 3, - 4, - 9 and - 6, range: - 5, - 7, - 19 and - 11.
C. It is not a function.
D. It is a function, domain: 3, 4, 9 and 6, range: 5, 7, and 11.

Step: 1

A relation is a function if every input has exactly one output.

Step: 2

The relation given is a function.

Step: 3

The domain is - 3, - 4, - 9 and - 6, range is - 5, - 7, - 19 and - 11

Correct Answer is : It is a function, domain: - 3, - 4, - 9 and - 6, range: - 5, - 7, - 19 and - 11.

Q14Determine whether the relation represented by the set of ordered pairs below is a function. Give the domain and range, if it is a function.
(5, - 7), (5, 8), (5, - 9), (7, 10).

A. It is a function, domain: 5, 8, and 10, range: - 7, 8, - 9 and 10
B. It is a function, domain: 5 and 7, range: - 7, 8, - 9 and 10
C. It is not a function
D. It is a function, domain: 5 and 7, range: 6, - 7, 8, - 9 and 10

Step: 1

A relation is a function if every input has exactly one output.

Step: 2

The relation is not a function because the input 5 has three outputs: - 7, 8, and - 9.

Correct Answer is : It is not a function

Q15Determine whether the relation represented in the graph is a function or not. Find the domain and range, if it is a function.

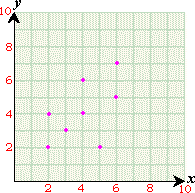
A. It is a function, domain: 2, 3, 4, 5, and 6 range: 2, 3, 4, 6, and 7.
B. It is a function, domain: 2, 4, and 6 range: 4, 6, and 8.
C. It is not a function.
D. It is a function, domain: 2, 3, 4, 5, and 6 range: 2, 3, 4, 5, and 7.

Step: 1

A relation is said to be a function if every input has exactly one output.

Step: 2

The inputs 2, 4, and 6 have more than one output.

Step: 3

So, the relation is not a function.

Correct Answer is : It is not a function.

Related Worksheet

Related Topic

Relation