Solved Examples and Worksheet for Representing Exponential Functions Using Tables or Graphs

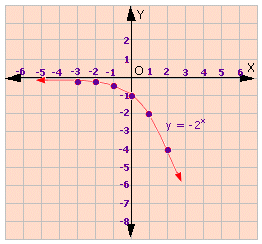
Q1Using the graph, find the domain and the range of the function y = - 2x.


A. Domain is set of all positive numbers and the range is set of all real numbers.
B. Domain is set of all negative numbers and the range is set of all negative numbers.
C. Domain is set of all real numbers and the range is set of all positive numbers.
D. Domain is set of all real numbers and the range is set of all negative numbers.

Solutions
Share 
Step: 1
From the graph of the function, y = -2x is defined for all x-values but only has y values that are less than 0.
Step: 2
The domain of y = -2x is the set of all real numbers and the range is the set of all negative numbers.
Correct Answer is :   Domain is set of all real numbers and the range is set of all negative numbers.
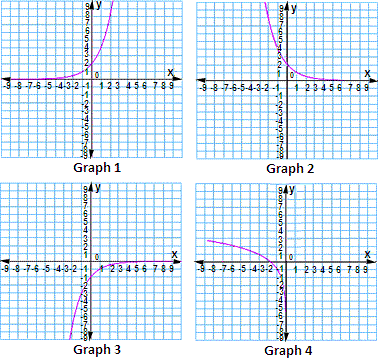
Q2Which of the following graphs represent the exponential function
y = 2(2)x?


A. Graph 4
B. Graph2
C. Graph 3
D. Graph 1

Solutions
Share 
Step: 1
Make a table of values that includes both positive and negative x values. Be sure to follow the order of operations when evaluating the function.
Step: 2
y = 2(2)x
  [Original exponential function.]
Step: 3
Substitute the values - 2, - 1, 0, 1, 2 and 3 for x in the function y = 2(2)x.
Step: 4
y = 2(2)-2
  [Replace x with -2.]
Step: 5
= 2(14) = 0.5
  [Use definition of negative exponent.]
Step: 6
y = 2(2)-1
  [Replace x with -1.]
Step: 7
= 2(12) = 1
  [Use definition of negative exponent.]
Step: 8
y = 2(2)0
  [Replace x with 0.]
Step: 9
= 2 × 1 = 2
  [20 = 1.]
Step: 10
y = 2(2)1 = 2 × 2 = 4
  [Replace x with 1.]
Step: 11
y = 2(2)2 = 2 × 4 = 8
  [Replace x with 2.]
Step: 12
y = 2(2)3 = 2 ×8 = 16
  [Replace x with 3.]
Step: 13

Step: 14
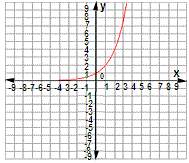
Draw a coordinate plane and plot the six points given by the table. Then draw a smooth curve through the points.
Step: 15
So, the graph of the exponential function y = 2(2)x matches with the Graph 1.
Correct Answer is :   Graph 1
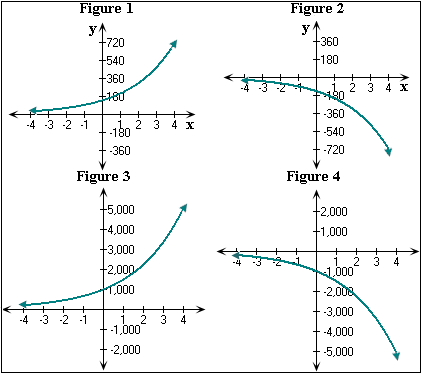
Q3The number of viewers Y(in millions) of a sports channel can be modeled by Y = 140(1.5)x where x = 0 represents the year 1998. Choose the graph that represents the model.

A. Figure 1
B. Figure 3
C. Figure 4
D. Figure 2

Solutions
Share 
Step: 1
Draw a table for the number of viewers of a sports channel in 1996, 1997, 1998, 1999, 2000, 2001, 2002. x value for these years will be - 2, - 1, 0, 1, 2, 3, 4.
x- 2- 101234
y62.293.3140210315472.5708.8
Step: 2
Draw a coordinate plane and plot the points given by table. Then draw a smooth curve through the points.
Step: 3
Notice that the graph has y-intercept of 140, and that it gets closer to negative side of the x-axis as the x values decrease.
Step: 4

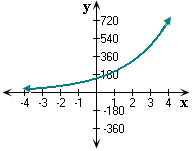
Step: 5
So, the graph of the number of viewers of the sports channel y = 140(1.5)x matches with the Figure 1.
Correct Answer is :   Figure 1
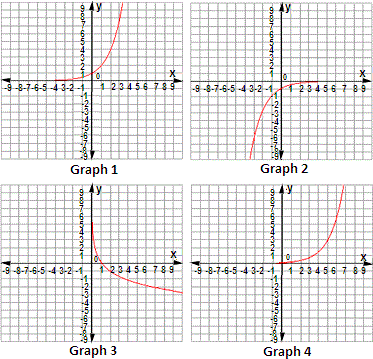
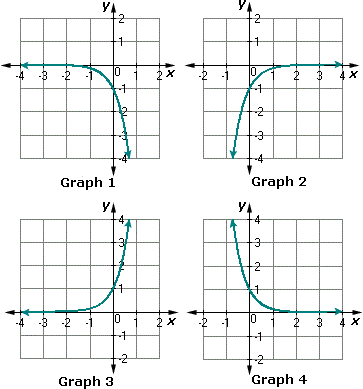
Q4Which of the graphs represents the exponential function y = (12)- x?


A. Graph 4
B. Graph 2
C. Graph 1
D. Graph 3

Solutions
Share 
Step: 1
Make a table of values that includes both positive and negative x values. Be sure to follow the order of operations when evaluating the function.
Step: 2
y = (12) - x
  [Original exponential function.]
Step: 3
Substitute the values - 2, - 1, 0, 1, 2 and 3 for x in the function y = (12) - x
Step: 4
y = (12)2
  [Replace x with -2.]
Step: 5
= 14 = 0.25
Step: 6
y = (12) 1
  [Replace x with -1.]
Step: 7
= 12 = 0.5
Step: 8
y = (12) 0
  [Replace x with 0.]
Step: 9
= 1
  [(12)0 = 1.]
Step: 10
y = (12)- 1
  [Replace x with 1.]
Step: 11
= 1(12) = 2
  [Use definition of negative exponent.]
Step: 12
y = (12) -2 = 1(12)2 = 1(14) = 4
  [Replace x with 2 and use definition of negative exponent.]
Step: 13
y = (12) - 3 = 1(12) 3 = 1(18) = 8
  [Replace x with 3 and use definition of negative exponent.]
Step: 14

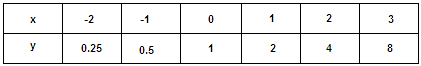
Step: 15
Draw a coordinate plane and plot the six points given by the table. Then draw a smooth curve through the points.
Step: 16
So, the graph 1 matches with given exponential function.
Correct Answer is :   Graph 1
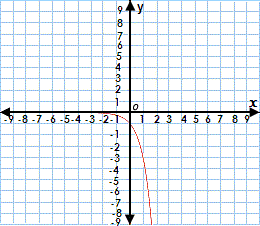
Q5Use the graph shown to find the domain and the range of the function. y = - (4x).

A. The domain is all positive real numbers and the range is all real numbers.
B. The domain is all real numbers and the range is all positive real numbers.
C. The domain is all real numbers and the range is all negative real numbers.
D. The domain is all negative real numbers and the range is all negative real numbers.

Solutions
Share 
Step: 1
From the graph of the function, y = - (4x) is defined for all x values but only has y values that are less than 0.
Step: 2
The domain of y = - (4x) is the set of all real numbers and the range is the set of all negative numbers.
Correct Answer is :   The domain is all real numbers and the range is all negative real numbers.
Q6To which axis does the graph of the exponential function y = 6 (3)x gets closer as the x-values decrease?

A. Positive y-axis
B. Positive x-axis
C. Negative y-axis
D. Negative x-axis

Solutions
Share 
Step: 1
Make the table of values for the equation y = 6 (3)x.
x- 3- 2- 1012
y29 23 261854
Step: 2
Draw a coordinate plane and plot the six points given by the table.
Step: 3
Draw a smooth curve through the plotted points.
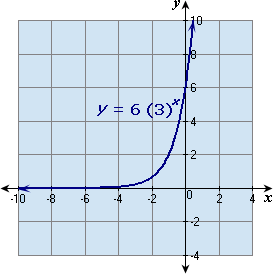
Step: 4
The graph gets closer to the negative side of the x-axis as the x-values decrease.
Correct Answer is :   Negative x-axis
Q7Which of the graphs represents the exponential function y = - 12(7)x?

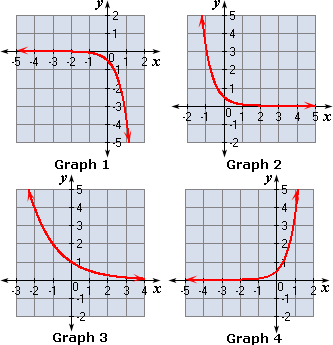
A. Graph 2
B. Graph 3
C. Graph 4
D. Graph 1

Solutions
Share 
Step: 1
y = - 12 (7)x
  [Original function.]
Step: 2
Take some values for x, such as - 3, - 2, - 1, 0, 1 and substitute in the given function to get the coordinates.
Step: 3
f(- 3) = - 12 (7)- 3
  [Substitute - 3 for x.]
Step: 4
= - 0.001
  [Simplify.]
Step: 5
f(- 2) = - 12 (7)- 2
  [Substitute - 2 for x.]
Step: 6
= - 0.01
  [Simplify.]
Step: 7
f(- 1) = - 12 (7)- 1
  [Substitute - 1 for x.]
Step: 8
= - 0.07
  [Simplify.]
Step: 9
f(0) = - 12 (7)0
  [Substitute 0 for x.]
Step: 10
= - 0.5
  [Simplify.]
Step: 11
f(1) = - 12 (7)1
  [Substitute 1 for x.]
Step: 12
= - 3.5
  [Simplify.]
Step: 13
Plot these values in a graph.
Step: 14
Among the graphs, Graph 1 represents the exponential function f(x) = - 12 (7)x.
Correct Answer is :   Graph 1
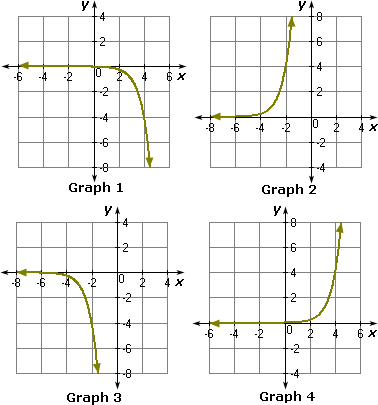
Q8Find the graph representing the equation y = 4x - 3.


A. Graph 2
B. Graph 4
C. Graph 1
D. Graph 3

Solutions
Share 
Step: 1
Make a table of values that includes both positive and negative x values.
x- 101234
y0.0040.0160.06250.2514
Step: 2
Graph the ordered pairs in the table shown and connect the points with a smooth curve.
Step: 3
Then the graph obtained is as shown in Graph 4.
Step: 4
So, Graph 4 represents the equation y = 4x - 3.
Correct Answer is :   Graph 4
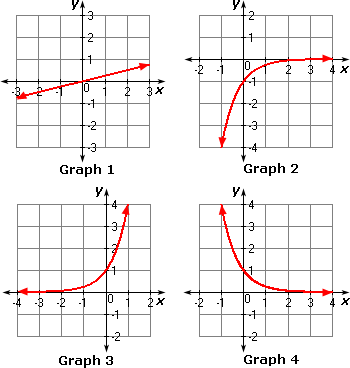
Q9Which graph represents the equation y = - (14 )x?

A. Graph 1
B. Graph 2
C. Graph 4
D. Graph 3

Solutions
Share 
Step: 1
Make a table of values that includes both positive and negative x values.
x- 10123
y- 4- 1- 0.25- 0.0625- 0.016
Step: 2
Graph the ordered pairs in the table shown and connect the points with a smooth curve.
Step: 3
Then the graph obtained matches with Graph 2.
Step: 4
So, Graph 2 represents the equation y = - (14 )x.
Correct Answer is :   Graph 2
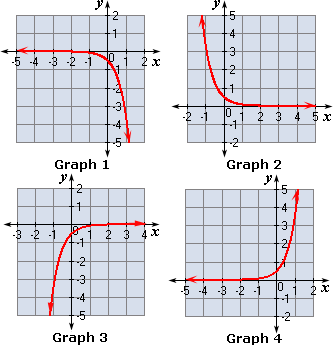
Q10Which of the graphs represents the exponential function y =   12(7)-x?

A. Graph 2
B. Graph 3
C. Graph 1
D. Graph 4

Solutions
Share 
Step: 1
y =   12 (7)-x
  [Original function.]
Step: 2
Take some values for x, such as - 3, - 2, - 1, 0, 1 and substitute in the given function to get the coordinates.
Step: 3
f(- 3) =   12 (7)3
  [Substitute - 3 for x.]
Step: 4
= 171.5
  [Simplify.]
Step: 5
f(- 2) =   12 (7)2
  [Substitute - 2 for x.]
Step: 6
= 24.5
  [Simplify.]
Step: 7
f(- 1) =   12 (7)1
  [Substitute - 1 for x.]
Step: 8
= 3.5
  [Simplify.]
Step: 9
f(0) =   12 (7)0
  [Substitute 0 for x.]
Step: 10
= 0.5
  [Simplify.]
Step: 11
f(1) =   12 (7)-1
  [Substitute 1 for x.]
Step: 12
= 0.07
  [Simplify.]
Step: 13
Plot these values in a graph.
Step: 14
Among the graphs, Graph 2 represents the exponential function f(x) =   12 (7)-x.
Correct Answer is :   Graph 2
Q11Use the graph shown to find the domain and range of the function y = 4(2)x.


A. domain is all real numbers and the range is all positive real numbers.
B. domain is all negative numbers and the range is all negative real numbers.
C. domain is all real numbers and the range is all real numbers.
D. domain is all positive real numbers and the range is all real numbers.

Solutions
Share 
Step: 1
The graph of the function, y = 4(2)x is defined for all x values, but only has y values that are greater than 0.
Step: 2
So, the domain of y = 4(2)x is all real numbers and the range is all positive real numbers.
Correct Answer is :   domain is all real numbers and the range is all positive real numbers.
Q12Find the graph representing the equation y = 7x.


A. Graph 1
B. Graph 2
C. Graph 4
D. Graph 3

Solutions
Share 
Step: 1
Make a table of values that includes both positive and negative x values.
x- 3- 2- 10
y0.0030.020.1431
Step: 2
Graph the ordered pairs in the table shown and connect the points with a smooth curve.
Step: 3
Then the graph obtained matches with Graph 3.
Step: 4
So, Graph 3 represents the equation y = 7x.
Correct Answer is :   Graph 3
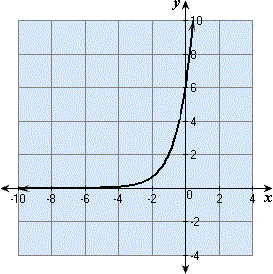
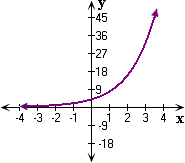
Q13Choose the equation that represents the given graph.


A. y = 6(2x)
B. y = 6(3x)
C. y = 2(3x)
D. y = 3(3x)

Solutions
Share 
Step: 1
Let the exponential equation be y = y0( 1 + r)x
Step: 2
6 = y0(1 + r)0 and hence y0 = 6
  [From the graph, substitute the point (0,6) in the general equation]
Step: 3
( 1 + r) -1 = 2y0
Step: 4
= y0(1 + r) - 1
  [From the graph,substitute the point ( - 1,2) in the general equation]
Step: 5
(1 + r) -1 = 26
  [ From step 2, y0 = 6]
Step: 6
1 + r = (0.3333) -1 = 3.000 = 3
  [Simplify]
Step: 7
Therefore, the equation is y = 6(3) x
  [Step 1, 2 and 5]
Correct Answer is :   y = 6(3x)
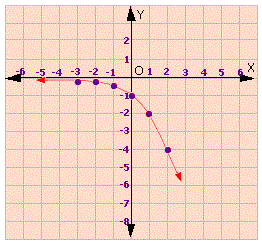
Q14Choose the equation which represents the given graph.


A. y = - (3x)
B. y = (2x)
C. y = - (2x)
D. y = (3x)

Solutions
Share 
Step: 1
Let the exponential equation be y = y 0 (1 + r)x
Step: 2
- 1 = y0(1 + r)0 and hence y0 = -1
  [ From the graph, substitute the point ( 0 , -1 ) in the general equation]
Step: 3
- 2 = y 0(1 + r)1
  [From the graph, substitute the point ( 1,- 2 ) in the general equation]
Step: 4
(1 + r)1 = - 2y0
Step: 5
(1 + r)1 = - 2- 1
  [From step 2, y0 = - 1]
Step: 6
1 + r = 2
  [Simplify]
Step: 7
Therefore , the equation is y = - (2x)
  [Step 1,2 and 5]
Correct Answer is :   y = - (2x)

HighSchool Math