Solved Examples and Worksheet for Comparing Properties of Two Functions

Q1Which function has a negative slope?
XY
030
127
224
321
418
i.) The table shows the amount of money left from each week. Initially Mary has $30 with her. She spends $3 per week.
ii.) The function whose input and output are related by Y = 2x + 4
A. (i)
B. Neither (i) nor (ii)
C. (ii)
D. Both (i) and (ii)

Solutions
Share 
Step: 1
From function1, Mary has $30 and spends money each week. The amount of money left from her and $3 decreases each week.
Step: 2
So, the graph has a negative slope of -3.
Step: 3
From function 2, y = 2x +4 which is in the form of y = mx + c. This function has a positive slope of 2.
Step: 4
Function 1 has a negative slope.
Correct Answer is :   (i)
Q2Which of the following functions has a greater rate of change?
(i) The school book store rents graphing calculators for $4 per month. It also collects a non- refundable fee of $5 for the school year. The total cost y of renting a calculator is modeled by function 1 where x denotes the number of months.
(ii) The graph of function 2 is as shown.


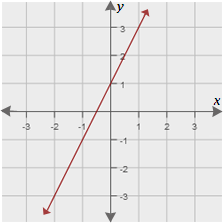
A. Both functions have equal rate of change
B. Function 1
C. Function 2

Solutions
Share 
Step: 1
The graph of function 2 contains (0, 1) and (1, 3).
  [From graph]
Step: 2
So, slope of the graph that represents function 2 = 3 - 11 - 0 = 21 = 2
  [m = y2 - y1x2 - x1]
Step: 3
So, the rate of change of function 2 is 2.
Step: 4
From the description of function 1, it can be represented as y = 4x + 5, where y denotes total cost of renting and x denotes number of months.
Step: 5
So, the rate of change of function 1 is 4.
Step: 6
Therefore, function 1 has greater rate of change.
  [4 > 2]
Correct Answer is :   Function 1
Q3Which of the following function has inverse
(i) Function 1 is given by y = 3x + 10.
(ii) Function 2 is represented by the table shown.
x12345
y1491625


A. Function 1
B. Both the function have inverses
C. Function 2

Solutions
Share 
Q4Which of the following function/s is a linear function ?
(i) Function 1 is represented by the table shown.
x12345
y 34567

(ii)The graph of function 2 is a shown.


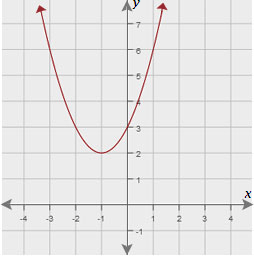
A. Both functions
B. Function 2
C. Function 1

Solutions
Share 
Step: 1
Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.
Step: 2
From the table, change in output values = 1
Step: 3
Change in input values = 1
Step: 4
Rate of change = Change in output valuesChange in input values = 11 = 1
Step: 5
Working backwards with the values in the table, we get (0, 2). So, the y-intercept is 2.
Step: 6
So, the function 1 that satisfies the table is y = x + 2, which is a linear equation. So, function 1 is linear.
Step: 7
The graph of function 2 is in the form of a parabola. So it represents a quadratic function of the form y = ax2 + bx + c.
Correct Answer is :   Function 1
Q5Which of the following function/s is an even function ?
(i) Josh counted that the number of students who participated in different sports are 2, 4, 6, 8, and 10 respectively. The situation is modeled by function 1 as y = 2x.
(ii)The graph of function 2 is as shown.


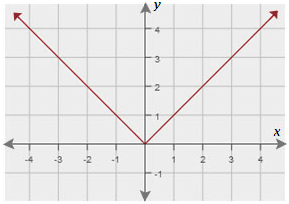
A. Function 1
B. Function 2
C. Both functions

Solutions
Share 
Step: 1
A function such that f(x) = f(- x) where the value remains unchanged if the sign of the independent variable is reversed.
Step: 2
If we observe the given functions 1 and 2, we will notice that Function 2 is an even function.
Correct Answer is :   Function 2
Q6Which of the following functions has a constant rate of change?
(i) Wilma had $8 with her. She sold x cards at $4 each and earned some money. The money she had with her finally is modeled by function 1 is y = 4x + 8.
(ii) Function 2 is given by y = x2.

A. Both functions
B. Function 2
C. Function 1

Solutions
Share 
Step: 1
Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.
Step: 2
Function 1 is given by y = 4x + 8. So, rate of change of function 1 is 4, which is a constant.
Step: 3
The function 2, y = x2 is a quadratic function. So, it has no constant rate of change.
  [Nonlinear functions are functions that do not have constant rate of change.]
Step: 4
So, function 1 has a constant rate of change.
Correct Answer is :   Function 1
Q7Which of the following function is an increasing function?
(i) Function 1 is represented by the table that shows the relationship between time and volume for a tank that is filling with water.
Time12345
Volume48121620

(ii) Function 2 is given by y = -2x + 5.

A. Function 2
B. Both functions
C. Function 1

Solutions
Share 
Step: 1
Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.
Step: 2
From the table, change in output values = 4
Step: 3
Change in input values = 1
Step: 4
Rate of change = Change in output valueschange in input values = 41 = 4
Step: 5
Working backwards with the values in the table, we get (0, 0). So, the y-intercept is 0.
Step: 6
So, the function 1 that satisfies the table is y = 4x, which is a linear equation.
Step: 7
Function 2 is given by y = -2x + 5, which is in the form y = a + bx. So, it is also a linear function.
Step: 8
If the graph of a function has positive slope, then that function is said to be an increasing function.
Step: 9
Slope of function 1 is 4(>0). So it is an increasing function.
Step: 10
Slope of function 2 is -2(<0). So it is not an increasing function.
Correct Answer is :   Function 1
Q8Which of the following function is a decreasing function?
(i) Function 1 is represented by the table that shows the relationship between the age of a mother and her child on her child's birthday.
Child's age12345
Mothers age2324252627

(ii) The graph of function 2 is as shown.


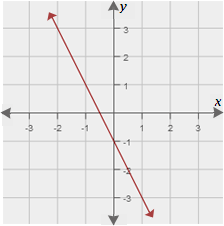
A. Function 1
B. Function 2
C. Both functions

Solutions
Share 
Step: 1
Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.
Step: 2
From the table, change in output values = 1
Step: 3
Change in input values = 1
Step: 4
Rate of change = Change in output valuesChange in input values = 11 = 1
Step: 5
Working backwards with the values in the table, we get (0, 22). So, the y-intercept is 22.
Step: 6
So, the function 1 that satisfies the table is y = x + 22, which is a linear equation.
Step: 7
The graph of function 2 contains (0, -1) and (-1, 1).
  [From graph]
Step: 8
So, slope of the graph that represents function 2 = 1-(-1)-1-0 = 2-1 = - 2.
  [m = y2 - y1x2 - x1]
Step: 9
The graph of function 2 contains (0, -1). So, the y - intercept is -1.
  [y-intercept is the y - value when x = 0]
Step: 10
So, the function 2 that satisfies the graph is y = -2x - 1, which is a linear equation. So, function 2 is linear.
Step: 11
If the graph of a function has positive slope, then that function is said to be an increasing function.
Step: 12
Slope of function 1 is 1(>0). So it is an increasing function.
Step: 13
Slope of function 2 is -2(<0). So it is a decreasing function.
Correct Answer is :   Function 2
Q9Which of the following function is an odd function?
(i) Function 1 is given by y = sin x.
(ii) The graph of function 2 is as shown.


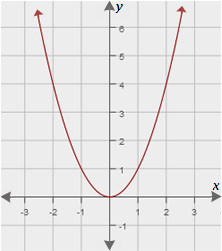
A. Both functions
B. Function 1
C. Function 2

Solutions
Share 
Step: 1
The graph of function 2 contains (-2, 4), (-1, 1), (0, 0), (1, 1) and (2, 4).
  [From graph]
Step: 2
From these points, it can be observed that y-coordinate of each point is equivalent the square of corresponding x - coordinate.
  [4 = (-2)2 = (2)2; 1 = (-1)2 = (1)2]
Step: 3
So, the function 2 that satisfies the graph is y = x2.
Step: 4
A function y = f(x) is said be an odd function, if f(-x) = -f(x), for all x in the domain of f.
Step: 5
Function 1 is given by y = f(x) = sin x
Step: 6
For function 1, f(-x) = sin(-x) = - sin x = - f(x)
Step: 7
So, function 1 is an odd function.
  [f(-x) = -f(x)]
Step: 8
For function 2, f(-x) = (-x)2 = x2 = f(x)
Step: 9
So, function 2 is an even function.
  [f(-x) = f(x)]
Correct Answer is :   Function 1
Q10Which of the following function has greatest integer function?
(i). The table shows the values of a function y = - [x]
XY
-11
00
1-1
2-2
3-3
(ii). The following linear model describes the time necessary to load a van with parcels for distribution. (Time to load the van) y = (a x number of parcels) + b→ y = 5 x + 6
Where 'a' represents the time per parcel and 'b' is a constant value representing the time for ancillary parts of the job.
A. Neither i nor ii
B. i
C. ii
D. Both i and ii

Solutions
Share 
Step: 1
From the function y = - [x] has greatest integer symbol. So this is a greatest integer function.
Correct Answer is :   i

HighSchool Math