Solved Examples and Worksheet for Graphing Linear Functions
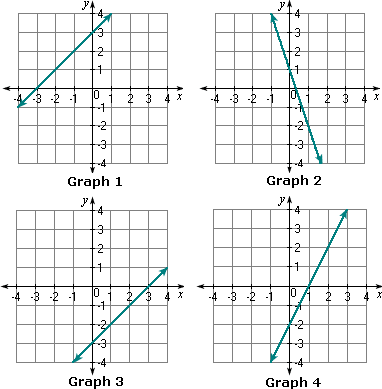
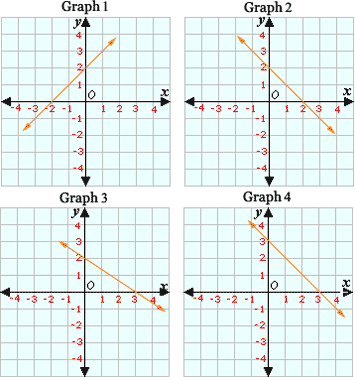
A. Graph 1
B. Graph 3
C. Graph 2
D. Graph 4
Step: 1
[Write the equation in slope- intercept form.]
Step: 2
The slope is - 3 and y
[m b
Step: 3
Plot the point (0, b b
Step: 4
Use the slope to locate a second point on line.
Step: 5
Step: 6
Draw a line through the two points.
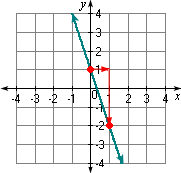

Step: 7
Graph of the equation y x
Correct Answer is : Graph 2
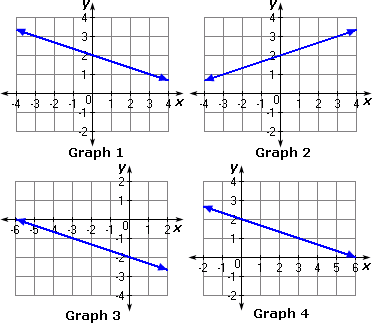
A. Graph 2
B. Graph 1
C. Graph 3
D. Graph 4
Step: 1
[Write the equation in slope-intercept form.]
Step: 2
The slope is 1 3 y
Step: 3
Plot the point (0, 2).
Step: 4
From (0, 2), move 1 unit up and 3 units right. You get another point (3, 3).
Step: 5
Draw a line through these two points.
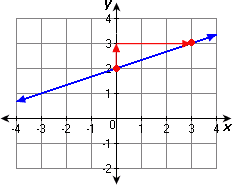

Step: 6
Graph of the equation x y
Correct Answer is : Graph 2
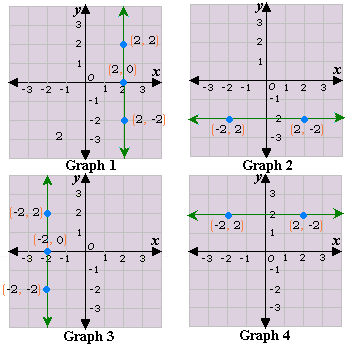
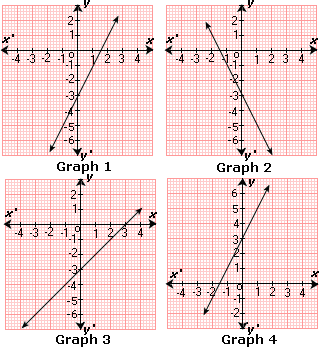
A. Graph 3
B. Graph 1
C. Graph 4
D. Graph 2
Step: 1
The x y
Step: 2
The graph of the equation x y
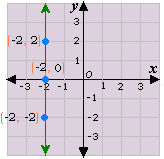

Step: 3
The above graph matches with the graph 3.
Correct Answer is : Graph 3
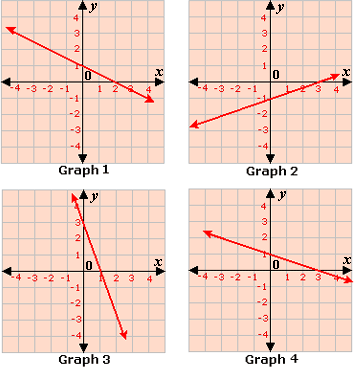
A. Graph 1
B. Graph 2
C. Graph 3
D. Graph 4
Step: 1
Step: 2
Choose values for x
Step: 3
When x y 1 3
[Substitute x
Step: 4
When x y 1 3
[Substitute x
Step: 5
When x y 1 3
[Substitute x
Step: 6
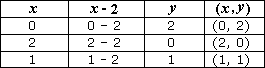
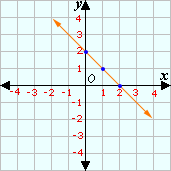
The points are, (0, - 1), (3, 0), and (- 3, - 2).
Step: 7
Draw a line passing through these points.
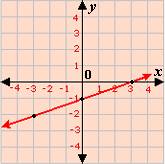

Step: 8
The above graph matches with Graph 2.
Correct Answer is : Graph 2
Step: 1
Calculate the values of y x
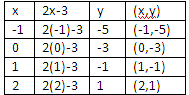
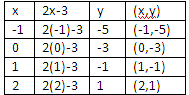
Step: 2
Plot the points on the graph.
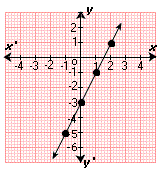

Step: 3
Therefore, Graph 1 represents the equation y x
Correct Answer is : Graph 1
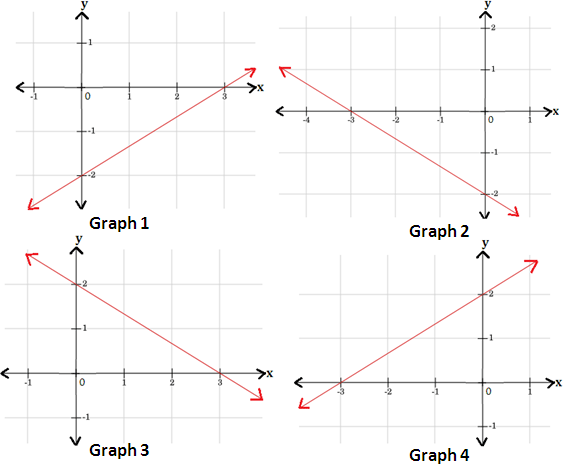
A. Graph 3
B. Graph 1
C. Graph 2
D. Graph 4
Step: 1
[Multiply by 2 on both sides of the equation.]
Step: 2
When x y 2 3
[Substitute x
Step: 3
When x y 2 3
[Substitute x
Step: 4
Thus, the points (0, -2) and (3, 0) are the solutions of the equation y 2 x 3
Step: 5
Draw a line passing through these points.
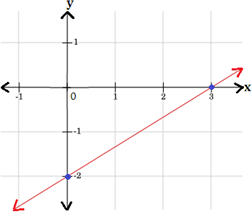

Step: 6
Therefore, graph 1, represents the equation y 2 x 3
Correct Answer is : Graph 1
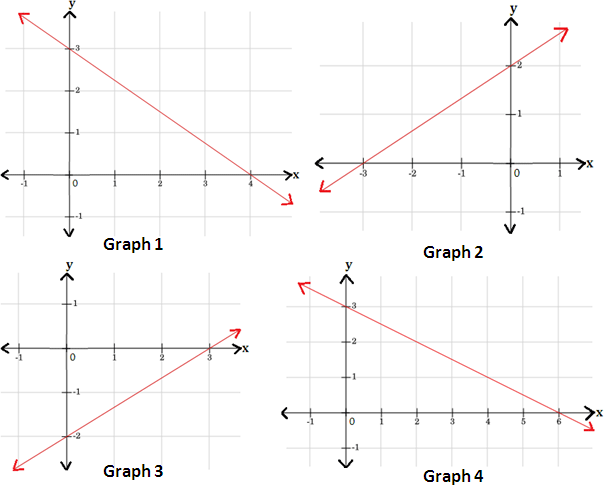
A. Graph 3
B. Graph 4
C. Graph 1
D. Graph 2
Step: 1
Step: 2
When x y 3 4
[Substitute x
Step: 3
When x y 3 4
[Substitute x
Step: 4
Thus, the points (0, 3) and (4, 0) are the solutions of the equation y 3 4 x
Step: 5
Draw a line passing through these points.
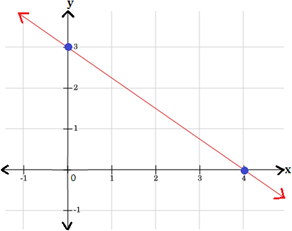

Step: 6
Therefore, graph 1 represents the equation y 3 4 x
Correct Answer is : Graph 1
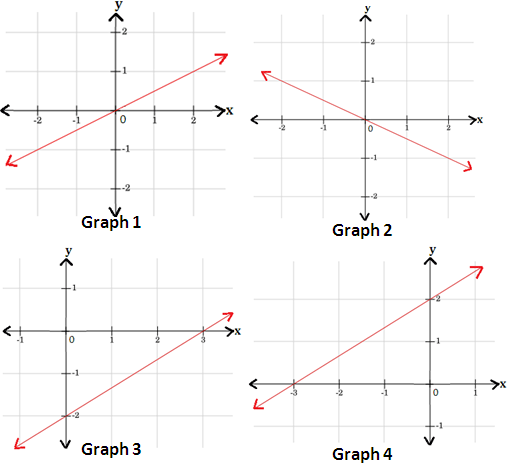
A. Graph 1
B. Graph 3
C. Graph 4
D. Graph 2
Step: 1
Step: 2
When x y 1 2
[Substitute x
Step: 3
When x y 1 2
[Substitute x
Step: 4
Thus, the points (2, - 1) and ( - 2, 1) are the solutions of the equation y 1 2 x
Step: 5
Draw a line passing through these points.
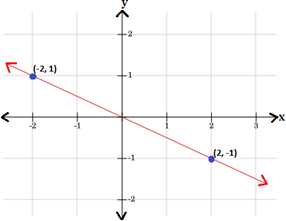

Step: 6
Therefore, graph 2 represents the equation y 1 2 x
Correct Answer is : Graph 2
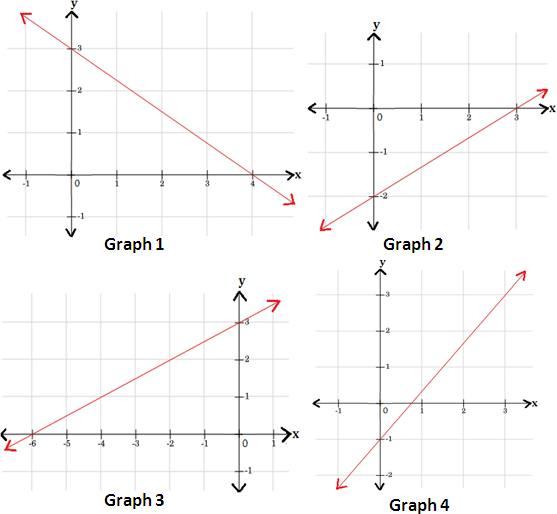
A. Graph 1
B. Graph 2
C. Graph 3
D. Graph 4
Step: 1
Step: 2
When x y 4 3
[Substitute x
Step: 3
When x y 4 3
[Substitute x
Step: 4
Thus, the points (0, - 1) and (3, 3) are the solution of the equation y 4 3 x
Step: 5
Draw a line passing through these points.
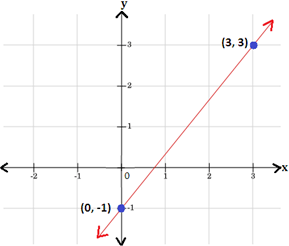

Step: 6
Therefore, graph 4, represents the equation y 4 3 x
Correct Answer is : Graph 4
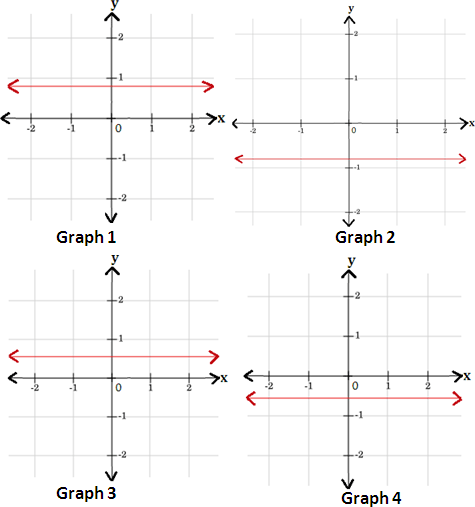
A. Graph 4
B. Graph 2
C. Graph 3
D. Graph 1
Step: 1
[Simplify the equation.]
Step: 2
The y x
Step: 3
Thus, the graph of the equation y x
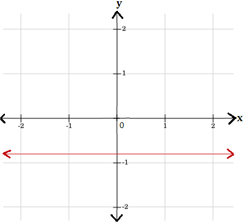

Step: 4
Therefore, graph 2 represents the equation y 4 5
Correct Answer is : Graph 2
- Determining a given Relation is a Function-Algebra1-Solved Examples
- Finding Values of a Function for a given Domain-Algebra1-Solved Examples
- Graphing Linear Functions for a Given Domain-Algebra1-Solved Examples
- Finding the Rate of Change-Algebra1-Solved Examples
- Finding Intercepts of a Linear Equation-Algebra1-Solved Examples
- Graphing Piecewise and Step Functions-Algebra1-Solved Examples
- Graphing Absolute Value Functions-Algebra1-Solved Examples
- Finding Intercepts of Quadratic Functions-Algebra1-Solved Examples
- Graphing and Analyzing Quadratic Functions-Algebra1-Solved Examples
- Identifying and Graphing Square Root Functions-Algebra1-Solved Examples
- Comparing Properties of Two Functions-Algebra1-Solved Examples
- Finding Intervals for Increasing and Decreasing Functions-Algebra1-Solved Examples
- Representing Exponential Functions Using Tables or Graphs-Algebra1-Solved Examples
- Graphing Logarithmic Functions-Algebra1-Solved Examples
- Graphing Trigonometric Functions-Algebra1-Solved Examples
- Identifying and Using Recursive Formula-Algebra1-Solved Examples
Related Worksheet
- Graph
- Linear Equation