Solved Examples and Worksheet for Finding the Rate of Change
| Year | Number of girls |
| 1998 | 2400 |
| 1999 | 3000 |
A. 4800
B. 5400
C. 6000
D. 4200
Step: 1
Average rate of change = C h a n g e i n t h e n u m b e r o f g i r l s a d m i t t e d i n s c h o o l C h a n g e i n t i m e
Step: 2
= 3 0 0 0 - 2 4 0 0 1 9 9 9 - 1 9 9 8
Step: 3
= 600 per year
Step: 4
So, the number of girls admitted in the year 2003 is 2400 + 5(600) = 5400
Correct Answer is : 5400
A. $42,000
B. $54,000
C. $60,000
D. $57,000
Step: 1
Average rate of change = C h a n g e i n t h e a n n u a l i n c o m e C h a n g e i n t i m e
Step: 2
= 3 6 0 0 0 - 3 0 0 0 0 1 9 9 8 - 1 9 9 6
Step: 3
= 6 0 0 0 2
Step: 4
So, the annual income of Jeff in the year 2004 is $(30,000 + 8(3,000)) = $54,000
Correct Answer is : $54,000
| Input( | - 1.2 | 0 | 0.6 | 1.5 | 2.4 | 3.1 | 3.6 |
| Output( | 3.2 | 2 | 1.4 | 0.5 | - 0.4 | - 1.1 | - 1.6 |
A. 0.42
B. 0.36
C. - 0.38
D. 0.38
Step: 1
Rate of change = c h a n g e i n o u t p u t v a l u e s c h a n g e i n i n p u t v a l u e s
Step: 2
| Input | Output | Change in input values | Change in output values | Rate of change |
| - 1.2 | 3.2 | |||
| 0 | 2 | 1.2 | - 1.2 | - 1 |
| 0.6 | 1.4 | 0.6 | - 0.6 | - 1 |
| 1.5 | 0.5 | 0.9 | - 0.9 | - 1 |
| 2.4 | - 0.4 | 0.9 | - 0.9 | - 1 |
| 3.1 | - 1.1 | 0.7 | - 0.7 | - 1 |
| 3.6 | - 1.6 | 0.5 | - 0.5 | - 1 |
Step: 3
The rate of change = - 1
Step: 4
The linear equation that represents the data is y x
Step: 5
Step: 6
When x y
Correct Answer is : - 0.38
A. 5000
B. 4000
C. 7000
D. 8000
Step: 1
The rate of increase is 250 per year.
Step: 2
Let t
Step: 3
The year 1995 is represented by t
Step: 4
This situation is represented by the linear equation y t
Step: 5
At t y
Step: 6
So, the number of students in the year 1995 is 5000.
Correct Answer is : 5000
| Hours | 1 | 2 | 3 | 4 | 5 |
| Earnings | 35 | 42 | 49 | 56 | 63 |
A. 10
B. 11
C. 8
D. 12
Step: 1
Rate of change = 4 2 - 3 5 2 - 1
Step: 2
This situation can be modeled by the linear equation y t
Step: 3
119 = 7 t t
Step: 4
Eddy needs to work for 13 hours.
Correct Answer is : 12
| Temperature(°C) | 10.5 | 8 | 5 | 0 |
| Altitude(in m) | 800 | 1300 | 1900 | 2900 |
A. 2
B. - 0.005
C. 0.05
D. 0.005
Step: 1
Rate of change of temperature = C h a n g e i n t e m p e r a t u r e C h a n g e i n a l t i t u d e 8 - 1 0 . 5 1 3 0 0 - 8 0 0
Step: 2
= - 2 . 5 5 0 0
Step: 3
= - 1 2 0 0
Step: 4
= - 0.005
Step: 5
So, the rate of change of temperature is - 0.005.
Correct Answer is : - 0.005
| Profit(in million $) | 59 | 71 | 83 | 95 |
| Years since 2000 | 1 | 2 | 3 | 4 |
A. 12
B. 2
C. 15
D. 5
Step: 1
Rate of change of profit = C h a n g e i n p r o f i t C h a n g e i n y e a r 7 1 - 5 9 2 - 1
Step: 2
= 1 2 1
Step: 3
= 12
Step: 4
So, the rate of change of profit is 12.
Correct Answer is : 12
| Salary(in $) | 1500 | 2100 | 2700 | 3300 |
| Years since 1997 | 1 | 2 | 3 | 4 |
A. $600
B. $150
C. $500
D. $200
Step: 1
Rate of change of salary = C h a n g e i n s a l a r y C h a n g e i n y e a r 2 1 0 0 - 1 5 0 0 2 - 1
Step: 2
= 6 0 0 1
Step: 3
= 600
Step: 4
So, the rate of change of salary is 600.
Correct Answer is : $600
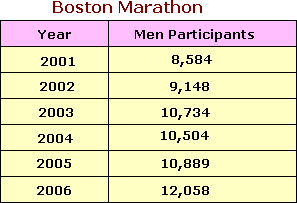
A. 500
B. 508.3
C. 608.3
D. 580.3
Step: 1
The rate that describes how one quantity changes in relation to another is called rate of change.
Step: 2
Rate of change = c h a n g e i n p a r t i c i p a n t s c h a n g e i n y e a r 1 0 8 8 9 - 9 1 4 8 2 0 0 5 - 2 0 0 2
Step: 3
= 1 7 4 1 3
Step: 4
= 580.3
Correct Answer is : 580.3
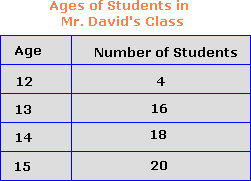
A. 3
B. 4
C. 5
D. 2
Step: 1
The rate that describes how one quantity changes in relation to another is called rate of change.
Step: 2
Rate of change = c h a n g e i n n u m b e r o f s t u d e n t s c h a n g e i n a g e 2 0 - 1 6 1 5 - 1 3
Step: 3
= 4 2
Step: 4
= 2
Correct Answer is : 2
- Determining a given Relation is a Function-Algebra1-Solved Examples
- Finding Values of a Function for a given Domain-Algebra1-Solved Examples
- Graphing Linear Functions for a Given Domain-Algebra1-Solved Examples
- Graphing Linear Functions-Algebra1-Solved Examples
- Finding Intercepts of a Linear Equation-Algebra1-Solved Examples
- Graphing Piecewise and Step Functions-Algebra1-Solved Examples
- Graphing Absolute Value Functions-Algebra1-Solved Examples
- Finding Intercepts of Quadratic Functions-Algebra1-Solved Examples
- Graphing and Analyzing Quadratic Functions-Algebra1-Solved Examples
- Identifying and Graphing Square Root Functions-Algebra1-Solved Examples
- Comparing Properties of Two Functions-Algebra1-Solved Examples
- Finding Intervals for Increasing and Decreasing Functions-Algebra1-Solved Examples
- Representing Exponential Functions Using Tables or Graphs-Algebra1-Solved Examples
- Graphing Logarithmic Functions-Algebra1-Solved Examples
- Graphing Trigonometric Functions-Algebra1-Solved Examples
- Identifying and Using Recursive Formula-Algebra1-Solved Examples
Related Worksheet
- Rate Of Change