Solved Examples and Worksheet for Factors of Whole Number to 100

Q1Find all the factors of 50.
A. 2, 5, 10 and 25
B. 1, 2, 5, 10 and 25
C. 1, 2, 5, 10, 25 and 50
D. 2, 5, 10, 25 and 50

Solutions
Share 
Step: 1
List the pairs of two numbers whose product is 50.
Step: 2
50 = 1 x 50
  
Step: 3
50 = 2 x 25
  
Step: 4
50 = 5 x 10
  
Step: 5
The factors of 50 are 1, 2, 5, 10, 25 and 50.
Correct Answer is :   1, 2, 5, 10, 25 and 50
Q2Find all the factors of 4.

A. 1, 2 and 4
B. 1, 3 and 4
C. 1, 2 and 5
D. 1, 2 and 6

Solutions
Share 
Step: 1
To find all the factors of 4, draw the rectangles that can be made from exactly 4 squares.
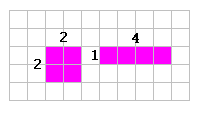
Step: 2
The dimensions of the rectangle show that the factors of 4 are 1, 2 and 4.
Correct Answer is :   1, 2 and 4
Q3Find all the factors of 6.
A. 1, 2, 3 and 7
B. 1, 3, 4 and 6
C. 1, 2, 3 and 6
D. 1, 2, 5 and 6

Solutions
Share 
Step: 1
To find all the factors of 6, draw the rectangles that can be made from exactly 6 squares.
Step: 2
For this, draw a 1 × 6 rectangle and 2 × 3 rectangle.
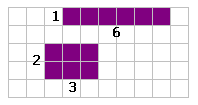
Step: 3
The dimensions of the rectangle show that the factors of 6 are 1, 2, 3 and 6.
Correct Answer is :   1, 2, 3 and 6
Q4Choose all the factors of 6.
A. 6, 12, 18
B. 1, 2, 3, 6
C. 3, 2
D. 1, 2, 3

Solutions
Share 
Step: 1
The number 6 is an even number, so it is divisible by 2.
Step: 2
It is also divisible by 3.
Step: 3
So, the factors of 6 are 1, 2, 3, 6.
Correct Answer is :   1, 2, 3, 6
Q5Choose the factors of 35.
A. 1, 5, 7, 35
B. 1, 2, 3, 4, 5, 6
C. 1, 3, 6, 10
D. 1, 2, 3, 4, 8, 10

Solutions
Share 
Step: 1
The number 35 ends with the digit 5, so it is divisible by 5.
Step: 2
So, the factors of 35 are 1, 5, 7, 35.
Correct Answer is :   1, 5, 7, 35
Q6Which of the following numbers is a factor of 18?
A. 3
B. 12
C. 8
D. 4

Solutions
Share 
Step: 1
The number 18 has digits whose sum is divisible by 3, it is divisible by 3.
Step: 2
So, 3 is a factor of 18.
Correct Answer is :   3
Q7Which of the following numbers is a factor of 26?

A. 2
B. 4
C. 5
D. 3

Solutions
Share 
Step: 1
The number 26 is an even number, so it is divisible by 2.
Step: 2
The digits of 26 do not add up to a number which is divisible by 3, so the number itself is not divisible by 3.
Step: 3
The number 26 does not end with 0 or 5, so it is not divisible by 5.
Step: 4
The number 26 is not divisible by 4.
Step: 5
So, 2 is a factor of 26.
Correct Answer is :   2
Q8Which of the following numbers is not a factor of 24?

A. 2
B. 6
C. 3
D. 5

Solutions
Share 
Step: 1
The number 24 is an even number, so it is divisible by 2.
Step: 2
The digits of 24 add up to 6, so it is also divisible by 3.
Step: 3
Therefore it must also be divisible by 6.
Step: 4
The number 24 is not divisible by 5 as it does not end with 0 or 5.
Step: 5
So, 5 is not a factor of 24.
Correct Answer is :   5
Q9Choose the list of factors of 28.
A. 2, 4, 7, 14, and 28
B. 1, 2, 14, and 28
C. 1, 2, 4, 7, 14, and 28
D. 0, 2, 4, 7, 14, and 28

Solutions
Share 
Step: 1
To find all the factors of 28, draw the rectangles that can be made from exactly 28 squares.
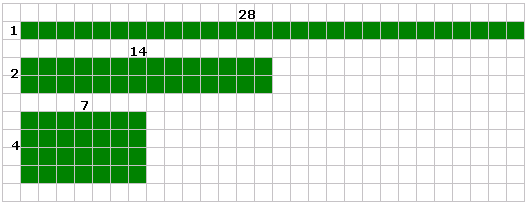
Step: 2
The number of squares along the sides of the rectangles are the factors of 28.
Step: 3
So, the factors of 28 are 1, 2, 4, 7, 14, and 28.
Correct Answer is :   1, 2, 4, 7, 14, and 28
Q10Find all the factors of 22.

A. only 2 and 11
B. only 1 and 22
C. only 1, 11, and 22
D. 1, 2, 11, and 22

Solutions
Share 
Step: 1
To find all the factors of 22, draw the rectangles that can be made from exactly 22 squares.
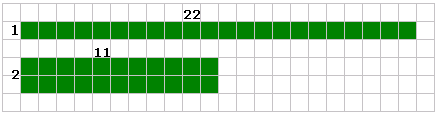
Step: 2
The number of squares along the sides of the rectangles are the factors of 22.
Step: 3
So, the factors of 22 are 1, 2, 11, and 22.
Correct Answer is :   1, 2, 11, and 22
Q11Choose all the factors of 93.

A. 1, 3, 31, 93
B. 1, 2, 4, 8, 11, 22, 44, 88
C. 1, 2, 4, 23, 46, 92
D. 93

Solutions
Share 
Step: 1
All the factors of 93 can be found by expressing the number as a product of two factors.
Step: 2
93 = 1 × 93, 3 × 31
  [Write the pairs of numbers with a product of 93.]
Step: 3
The factors of 93 are 1, 3, 31, 93.
Correct Answer is :   1, 3, 31, 93
Q12Find all the factors of 65.

A. 65
B. 1, 5, 13, 65
C. 1, 2, 4, 8, 16, 32, 64
D. 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Solutions
Share 
Step: 1
All the factors of 65 can be found by expressing the number as a product of two factors.
Step: 2
65 = 1 × 65, 5 × 13
  [Write the pairs of numbers with a product of 65.]
Step: 3
The factors of 65 are 1, 5, 13, 65.
Correct Answer is :   1, 5, 13, 65
Q13Find all the factors of 49.

A. 8, 7, 10 and 49
B. 1, 7 and 49
C. 7 and 49
D. 1, 7, 8 and 49

Solutions
Share 
Step: 1
All the factors of 49 can be found by expressing the number as a product of two factors.
Step: 2
49 = 1 × 49 = 7 × 7
Step: 3
So, the factors of 49 are 1, 7 and 49.
Correct Answer is :   1, 7 and 49
Q14Find all the factors of 83.
A. 1, 2, 41, 82
B. 83
C. 1, 2, 3, 6, 13, 26, 39, 78
D. 1, 83

Solutions
Share 
Step: 1
All the factors of 83 can be found by expressing the number as a product of two factors.
Step: 2
83 = 1 × 83
  [Write the pairs of numbers with a product of 83.]
Step: 3
So, the factors of 83 are 1, 83.
Correct Answer is :   1, 83

HighSchool Math