Solved Examples and Worksheet for Finding Areas of Rectilinear Figures
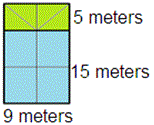
A. 205 square meters
B. 160 square meters
C. 120 square meters
D. 180 square meters
Step: 1
Divide the figure into two rectangles A and B, as shown below.
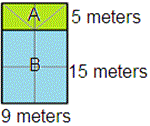

Step: 2
Rectangle A is 5 meters tall and 9 meters wide.
Therefore area of rectangle A = 5 × 9 = 45 square meters.
Therefore area of rectangle A = 5 × 9 = 45 square meters.
Step: 3
Now, rectangle B is 15 meters tall and 9 meters wide.
Therefore area of rectangle B = 15 × 9 = 135 square meters.
Therefore area of rectangle B = 15 × 9 = 135 square meters.
[Here two rectangles are of same width.]
Step: 4
Now add the areas of the two rectangles: 45 square meters + 135 square meters. = 180 square meters.
Step: 5
Therefore the total area of the window is 180 square meters. So the area of the curtain should be 180 square meters.
Correct Answer is : 180 square meters
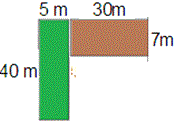
A. 360 square meters
B. 420 square meters
C. 480 square meters
D. 410 square meters
Step: 1
We can divide the figure into two rectangles. The brown colored rectangle represents
Play ground and green colored is Park.
Play ground and green colored is Park.
Step: 2
Multiply = 7 × 30
Therefore area of Play ground = 210 square meters.
Therefore area of Play ground = 210 square meters.
Step: 3
Multiply = 40 × 5
Therefore area of Park = 200 square meters.
Therefore area of Park = 200 square meters.
Step: 4
The total area of the figure = area of the Play ground + area of the Park = 210 square meters + 200 square meters.= 410 square meters.
Correct Answer is : 410 square meters
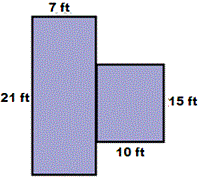
A. 295 square ft
B. 268 square ft
C. 245 square ft
D. 297 square ft
Step: 1
The given figure is a composite figure of two rectangles. Decompose the figure into two rectangles A and B.
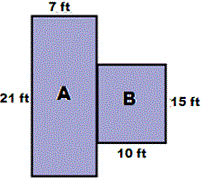

Step: 2
Start with rectangle A.
Rectangle A is 21 ft tall and 7 ft wide.
Rectangle A is 21 ft tall and 7 ft wide.
Step: 3
Multiply: 21 × 7 = 147 square ft.
Therefore the area of rectangle A is 147 square ft.
Therefore the area of rectangle A is 147 square ft.
Step: 4
Now, Look at rectangle B.
It is 15 ft tall and 10 ft wide.
It is 15 ft tall and 10 ft wide.
Step: 5
Multiply: 15 × 10 = 150 square ft.
The area of rectangle B is 150 square ft.
The area of rectangle B is 150 square ft.
Step: 6
Now add the areas of two rectangles : 147 square ft. + 150 square ft. = 297 square ft.
Therefore the total area occupied by the study room is 297 square ft.
Therefore the total area occupied by the study room is 297 square ft.
Correct Answer is : 297 square ft
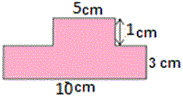
A. 25 square cm
B. 45 square cm
C. 35 square cm
D. 40 square cm
Step: 1
The given figure is a combined figure of two rectangles. Decompose the figure as two rectangles A and B, as shown below.
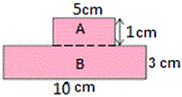

Step: 2
Length of the rectangle A is 5 cm and width is 1 cm.
Step: 3
Therefore area of the rectangle A = 5 × 1 = 5 square cm.
Step: 4
Now, length of the rectangle B is 10 cm and width is 3 cm.
Therefore area of the rectangle B = 10 × 3 = 30 square cm.
Therefore area of the rectangle B = 10 × 3 = 30 square cm.
Step: 5
The total area of the figure (A + B) = 5 + 30 = 35 square cm.
Correct Answer is : 35 square cm
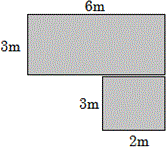
A. 24 square meters
B. 28 square meters
C. 20 square meters
D. 34 square meters
Step: 1
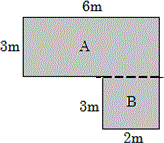
Divide the figure into two rectangles A and B, as shown below.

Step: 2
Length of the rectangle A is 6 m and width is 3 m.
Therefore area of rectangle A = 6 × 3 = 18 square meters.
Therefore area of rectangle A = 6 × 3 = 18 square meters.
Step: 3
Length of rectangle B is 3m and width is 2m.
Therefore area of rectangle B = 3 × 2 = 6 square meters.
Therefore area of rectangle B = 3 × 2 = 6 square meters.
Step: 4
Now add the areas of the two rectangles: 18 + 6 = 24 square meters.The total area of the bath room is 24 square meters.
Correct Answer is : 24 square meters

A. 15 square cm
B. 18 square cm
C. 16 square cm
D. 23 square cm
Step: 1
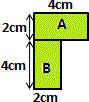
Decompose the given figure into two rectangles A and B, as shown bellow.
Step: 2
Step: 3
Start with rectangle A.
Rectangle A is 4 cm long and 2 cm wide.
Rectangle A is 4 cm long and 2 cm wide.
Step: 4
Multiply: 4 × 2 = 8 square cm.
Therefore the area of rectangle A is 8 square cm.
Therefore the area of rectangle A is 8 square cm.
Step: 5
Now, Look at rectangle B.
Rectangle B is 4 cm long and 2 cm wide.
Rectangle B is 4 cm long and 2 cm wide.
[Since the dimentions are same for both the cards.]
Step: 6
Multiply: 4 × 2 = 8 square cm.
The area of rectangle B is 8 square cm.
The area of rectangle B is 8 square cm.
Step: 7
Now add the areas of the two rectangles: 8 square cm. + 8 square cm. = 16 square cm.
Therefore the total area covered by the cards = 16 square cm.
Therefore the total area covered by the cards = 16 square cm.
Correct Answer is : 16 square cm
A. 150 square meters
B. 160 square meters
C. 180 square meters
D. 140 square meters
Step: 1
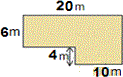
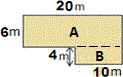
The given figure is a combined figure of two rectangles. Decompose the figure as two rectangles A and B, as shown below.

Step: 2
Here rectangle A represents the yard and B represents the pool.
Step: 3
Length of rectangle A is 20 m long and 6 m wide.
Therefore area of rectangle A = 20 × 6 = 120 square meters.
Therefore area of rectangle A = 20 × 6 = 120 square meters.
Step: 4
Length of rectangle B is 10 m long and 4 m wide.
Therefore area of rectangle B = 10 × 4 = 40 square meters.
Therefore area of rectangle B = 10 × 4 = 40 square meters.
Step: 5
Now add the areas of the two rectangles: 120 + 40 = 160 square meters. The total area of the yard and pool is 160 square meters.
Correct Answer is : 160 square meters
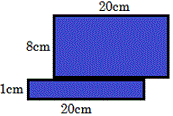
A. 160 square cm
B. 280 square cm
C. 180 square cm
D. 150 square cm
Step: 1
The given figure is a combined figure of two rectangular card boards. Decompose the figure as two rectangles A and B, as shown below.
Step: 2
Length of rectangle A is 20 cm and width is 8 cm.Therefore area of rectangle A = 20 × 8 = 160 square cm.
Step: 3
Now, length of rectangle B is 20 cm and width is 1 cm .Therefore area of rectangle B = 20 × 1 = 20 square cm.
Step: 4
The total area of the figure (A + B) = 160 + 20 = 180 square cm.
Correct Answer is : 180 square cm
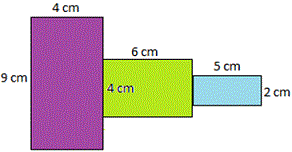
A. 83 square meters
B. 91 square meters
C. 70 square meters
D. 65 square meters
Step: 1
Divide the given figure into 3 rectangles; purple, green and blue.
Step: 2
Start with the purple colored rectangle. Length is 9 cm and width is 4 cm.
Therefore area = 9 × 4 = 36 square cm.
Therefore area = 9 × 4 = 36 square cm.
Step: 3
Take green colored rectangle. Length is 6 cm and width is 4 cm.
Therefore area = 6 × 4 = 24 square cm.
Therefore area = 6 × 4 = 24 square cm.
Step: 4
Now look at the blue rectangle. Length is 5 cm and width is 2 cm.
Therefore area = 5 × 2 = 10 square cm.
Therefore area = 5 × 2 = 10 square cm.
Step: 5
Now the total area of the picture = 36 + 24 + 10 = 70 square cm.
Correct Answer is : 70 square meters
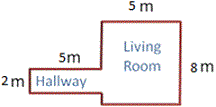
A. 18 square meters
B. 50 square meters
C. 35 square meters
D. 45 square meters
Step: 1
In order to find the total area of floor to be covered, you need to decompose the floor plan into two rectangles as Hallway and Living room as shown below.
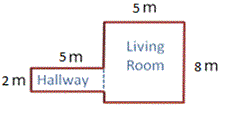

Step: 2
First start with Hallway: Length of Hallway is 5 m and width is 2 m.
Therefore area of Hallway = 5 × 2 = 10 square meters.
Therefore area of Hallway = 5 × 2 = 10 square meters.
Step: 3
Now, find the area of Living room: Length of Living room is 8 m and width is 5 m.
Therefore area of Living room = 8 × 5 = 40 square meters.
Therefore area of Living room = 8 × 5 = 40 square meters.
Step: 4
The total area of the floor = area of Hallway + area of Living room = 10 + 40 = 50 square meters.
Correct Answer is : 50 square meters
- Telling Time to the nearest Minute-Gr 3-Solved Examples
- Elapsed Time-Gr 3-Solved Examples
- Measuring Length Using Ruler-Gr 3-Solved Examples
- Estimating Metric Units-Gr 3-Solved Examples
- Using Operations to Solve Problems Involving Volume and Mass-Gr 3-Solved Examples
- Perimeter of Polygons-Gr 3-Solved Examples
- Finding an Unknown Dimension of a Polygon-Gr 3-Solved Examples
- Finding Area of Rectangles by Tiling-Gr 3-Solved Examples
- Area of Plane Figures - Counting Unit Squares-Gr 3-Solved Examples
- Solving Problems on Area of Rectangles-Gr 3-Solved Examples
- Representing Distributive Property Using Area Models-Gr 3-Solved Examples
- Rectangles with Same Area but Different Perimeters and Same Perimeter but Different Areas-Gr 3-Solved Examples
- Constructing Pictographs-Gr 3-Solved Examples
- Constructing Bar Graphs-Gr 3-Solved Examples
- Interpreting Bar Graphs-Gr 3-Solved Examples