Definition Of SAA Congruency Postulate

If two angles and the included side of one triangle are congruent to the two angles and the included side of another triangle, then the two triangles are congruent.

More About SAA Congruency Postulate

SAA postulate can also be called as AAS postulate.
The side between two angles of a triangle is called the included side of the triangle.
SAA postulate is one of the conditions for any two triangles to be congruent.

Video Examples: SAA Congruency Postulate

Example of SAA Congruency Postulate

The triangles ABC and PQR are congruent, i.e., ΔABC ≅ ΔPQR, since ∠CAB = ∠RPQ, AC = PR, and ∠ABC = ∠PQR.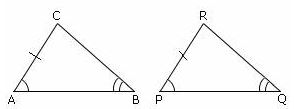

Solved Example on SAA Congruency Postulate

Ques: If the two triangles given are congruent by SAA postulate then identify the value of angle Q.

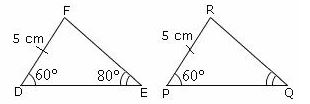
Choices:

A. 80°
B. 60°
C. 75°
D. 70°
Correct Answer: A

Solution:

Step 1: If two angles and the non-included side of one triangle is congruent to 
two angles and the non-included side of another triangle then the two triangles are congruent by SAA postulate.
Step 2: As the given triangles are congruent by SAA postulate 
∠FDE = ∠RPQ, DF= PR, and ∠DEF = ∠PQR.
Step 3: And given ∠DEF = 80° it implies ∠PQR = 80° by SAA postulate. 

Related Worksheet

• Unit-Rates-Gr-6
• Transformations-Gr-8
• Multiplying-Number-or-Decimal-with-Powers-of-10-Gr-5
• Application-of-Multi-Step-Problems-Gr-4
• Problems-on-Multiplication-and-Division-Involving-Unknown-Quantities-Gr-4