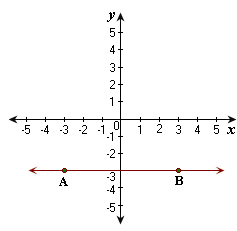Solved Examples and Worksheet for Slope of a Line from its Graph

Q1Graph a line and find the slope of the line passing through the points (1, 3) and (2, 4).
A. - 12
B. -1
C. 12
D. 1

Solutions
Share 
Step: 1
Plot the points on the graph
Step: 2
Slope = rise/run = 11
Step: 3
The slope of the line is 1.
Correct Answer is :   1
Q2Graph a line and find the slope of the line passing through the points (-1, -3) and (2, 4).
A. -7
B. 7
C. - 73
D. 73

Solutions
Share 
Step: 1
Plot the points on the graph
Step: 2
Slope = rise/run = 73
Step: 3
The slope of the line is 73 .
Correct Answer is :    73
Q3Graph a line and find the slope of the line passing through the points (- 1, 3) and (2, - 4).


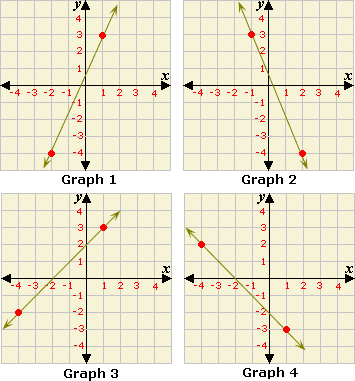
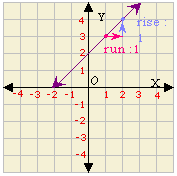
A. Graph 3, Slope = 1
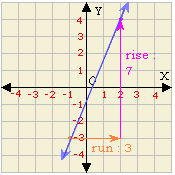
B. Graph 4, Slope = - 1
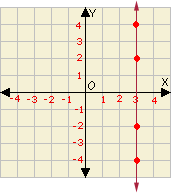
C. Graph 2, Slope = - 73
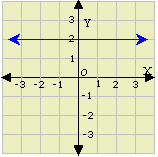
D. Graph 1, Slope = 73

Solutions
Share 
Step: 1
Plot the points on the graph and draw a line through them.
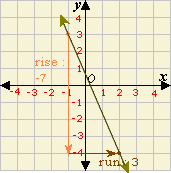
Step: 2
Slope = riserun = - 73
Step: 3
The slope of the line is - 73 .
Correct Answer is :   Graph 2, Slope = - 73
Q4The slope of the line in the graph is ______.

A. Undefined
B. Positive
C. Zero
D. Negative

Solutions
Share 
Step: 1
The line in the graph is vertical.
Step: 2
Slope = riserun.
The run is zero in the graph.
Step: 3
So, the slope of the line in the graph is undefined.
Correct Answer is :   Undefined
Q5Find the slope of the line AB as shown in the graph.

A. 6
B. Undefined
C. 0
D. 3

Solutions
Share 
Step: 1
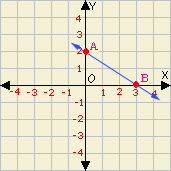
Slope of the line passes through the two points (x1, y1) and (x2, y2) is, m = y2-y1x2-x1.
Step: 2
The coordinates of the points A and B are (- 3, - 3) and (3, - 3).
  [From the graph.]
Step: 3
Slope of the line, AB = -3+33+3
  [(x1, y1) = (- 3, - 3) and (x2, y2) = (3, -3).]
Step: 4
= 06 = 0
  [Simplify.]
Step: 5
The slope of the line AB is 0.
Correct Answer is :   0
Q6Find the slope of the line in the graph.


A. 2
B. 5
C. 1
D. 3
E. 0

Solutions
Share 
Step: 1
The line in the graph is a horizontal line. Change in y-coordinate is zero.
Step: 2
Slope = change in ychange in x.
Step: 3
So, slope of the horizontal line is zero.
Correct Answer is :   0
Q7For which of the graphs does the slope of the line equal 2 and has (2, 0) on it?


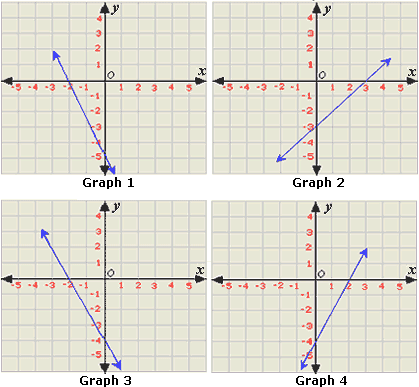
A. Graph 4
B. Graph 2
C. Graph 3
D. Graph 1

Solutions
Share 
Step: 1
Slope m = 2
Step: 2
One point on the line is (2, 0).
Step: 3
Slope = 2 = change in ychange in x
Step: 4
Choose some value for x1 and then find corresponding y1.
Step: 5
If x1 = 0, 2 = 0 -y12 - 0
Step: 6
0 - y1 = 4
Step: 7
y1 = - 4
Step: 8
So, (0, - 4) is another point on the line.
Step: 9
Indicate these two points on the line and draw a straight line passing through it as shown in Graph 4.
Step: 10
So, Graph 4 represents a line having slope 2 and (2, 0) on it.
Correct Answer is :   Graph 4
Q8Find the slope of the line shown in the graph.

A. 32
B. - 32
C. - 23
D. - 1

Solutions
Share 
Q9Find the slope of the line PQ shown in the graph.

A. - 12
B. - 2
C. 12
D. 2

Solutions
Share 
Step: 1
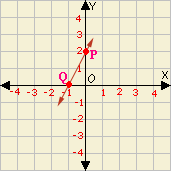
The coordinates of the point P are (0, 2) and coordinates of the point Q are (- 1, 0).
Step: 2
Slope = change in ychange in x
  [Use the formula.]
Step: 3
= 0 - 2- 1 - 0
  [Substitute the values.]
Step: 4
= 2
  [Simplify.]
Step: 5
The slope of the line PQ is 2.
Correct Answer is :   2
Q10Find the slope of the line PQ shown in the graph.


A. 2
B. - 23
C. 23
D. - 2

Solutions
Share 
Step: 1
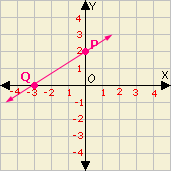
The coordinates of the point P are (0, 2) and coordinates of the point Q are (- 3, 0).
Step: 2
Slope = change in ychange in x
  [Use the formula.]
Step: 3
= 0 - 2- 3 - 0
  [Substitute the values.]
Step: 4
= 23
  [Simplify.]
Step: 5
The slope of the line PQ is 23.
Correct Answer is :   23

HighSchool Math