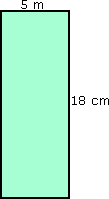Solved Examples and Worksheet for Problems Involving Areas of Rectangles

Q1The length of a rectangular sheet of paper is 27 centimeters and its perimeter is 86 centimeters. What is the area of the rectangle?
A. 431 square centimeters
B. 434 square centimeters
C. 433 square centimeters
D. 432 square centimeters

Solutions
Share 
Step: 1
The perimeter of a rectangle = 2(l + b) and the area of a rectangle = l × b, where l is its length and b is its breadth.
Step: 2
Let b be the width of the rectangular sheet of paper.
Step: 3
The perimeter of the rectangular sheet of paper = 2(27 + b) = 86.
  [Substitute 27 for l and 86 for perimeter.]
Step: 4
2(27+b)2=862
  [Divide each side by 2.]
Step: 5
(27 + b) = 43
  [Simplify.]
Step: 6
27 + b - 27 = 43 - 27
  [Subtract 27 from each side.]
Step: 7
b = 16
  [Simplify.]
Step: 8
The area of the paper = 27 × 16 = 432.
  [Multiply 27 with 16.]
Step: 9
So, the area of the rectangular sheet of paper is 432 square centimeters.
Correct Answer is :   432 square centimeters
Q2Quincy wants to lay a rectangular flowerbed of length 6 ft and width 5 ft. What would be its area?
A. 31 square ft
B. 29 square ft
C. 30 square ft
D. 35 square ft

Solutions
Share 
Step: 1
The area of a rectangle = length × width.
  [Formula.]
Step: 2
The flowerbed that Quincy wants is in the shape of a rectangle.
Step: 3
The area of the flowerbed = 6 × 5
  [Substitute the values.]
Step: 4
= 30
  [Multiply.]
Step: 5
The area of the flowerbed is 30 square ft.
Correct Answer is :   30 square ft
Q3The area of a rectangle is 35 square inches. The width of the rectangle is 5 inches. What is the length of the rectangle?
A. 175 in.
B. 30 in.
C. 5 in.
D. 7 in.

Solutions
Share 
Step: 1
Length of a rectangle = area of rectangle ÷ width of rectangle.
  [Formula for length of the rectangle.]
Step: 2
= 35 ÷ 5 = 7
  [Substitute the values of area and width.]
Step: 3
The length of the rectangle is 7 in..
Correct Answer is :   7 in.
Q4Find the area(A) of a rectangle with length(l) = 32 in. and width(w) = 31 in. using the formula A = lw.

A. 993 in.2
B. 992 in.2
C. 994 in.2
D. 991 in.2

Solutions
Share 
Step: 1
The formula for the area of a rectangle, A = lw.
Step: 2
The area of the rectangle = 32 in × 31 in
  [Substitute the values for l = 32 in and w = 31 in]
Step: 3
= 992 in.2
Correct Answer is :   992 in.2
Q5Lucy wants to lay a rectangular flowerbed of length 4 m and breadth 3 m. What would be its area?

A. 7 m2
B. 12 m2
C. 8 m2
D. 16 m2

Solutions
Share 
Step: 1
Length of the flowerbed = 4 m
Breadth of the flowerbed = 3 m
  [Given.]
Step: 2
Area of a rectangle = length × breadth
Step: 3
= 4 m × 3 m
Step: 4
= 12 m2
Step: 5
The area of the flowerbed is 12 m2.
Correct Answer is :   12 m2
Q6Find the area of a rectangle of length 13 cm and breadth 8 cm.

A. 114 cm2
B. 109 cm2
C. 99 cm2
D. 104 cm2

Solutions
Share 
Step: 1
Length of the rectangle = 13 cm
Breadth of the rectangle = 8 cm
Step: 2
Area of the rectangle = length × breadth
Step: 3
= 13 cm × 8 cm
Step: 4
= 104 cm2
Step: 5
So, the area of the rectangle is 104 cm2.
Correct Answer is :   104 cm2
Q7The length of a rectangular field is 24 m and its area is 120 m2. Find the breadth of the field.
A. 7 m
B. 4 m
C. 6 m
D. 5 m

Solutions
Share 
Step: 1
Area of a rectangle = length × breadth
Step: 2
Area of the rectangle = 120 m2
  [Given.]
Step: 3
So, 24 m × breadth = 120 m2
Step: 4
breadth = 120 m224 m
Step: 5
= 5 m
  [Divide.]
Step: 6
So, the breadth of the field is 5 m.
Correct Answer is :   5 m
Q8Find the area of the rectangle.


A. 112 mm2
B. 56 mm2
C. 122 mm2
D. 192 mm2

Solutions
Share 
Step: 1
Area of a rectangle = length × width
  [Formula.]
Step: 2
Area of the rectangle = 12 mm × 16 mm = 192 mm2
  [Substitute the values and simplify.]
Step: 3
Therefore, the area of the rectangle is 192 mm2.
Correct Answer is :   192 mm2
Q9Find the area of the rectangle.


A. 80 cm2
B. 56 cm2
C. 90 cm2
D. 112 cm2

Solutions
Share 
Step: 1
Area of a rectangle = length × breadth
  [Formula.]
Step: 2
Area of the rectangle = 18 cm × 5 cm = 90 cm2
  [Substitute the values and simplify.]
Step: 3
Therefore, the area of the rectangle 90 cm2.
  [Substitute the values and simplify.]
Correct Answer is :   90 cm2
Q10The area of a rectangular drawing room is 18 m2. If its length is 6 m, find the width of the drawing room.
A. 12 m
B. 6 m
C. 3 m
D. 9 m

Solutions
Share 
Step: 1
Area of drawing room = 18 m 2
Step: 2
Length of the drawing room = 6 m
Step: 3
Width of the drawing room = (AreaLength) m
= (186) m = 3 m
Step: 4
So, the width of the drawing room is 3 m.
Correct Answer is :   3 m

HighSchool Math