Quadratic Function
Definition Of Quadratic Function
Quadratic function is a function that can be described by an equation of the form f(x) = ax2 + bx + c, where a ≠ 0.
In a quadratic function, the greatest power of the variable is 2. The graph of a quadratic function is a parabola.
More About Quadratic Function
Quadratic equation: An equation in the standard form ax2 + bx + c = 0, where a ≠ 0 is called a quadratic equation.
Quadratic formula: A quadratic formula is the solution of a quadratic equation ax2 + bx + c = 0, where a ≠ 0, given by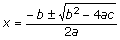
Quadratic inequality: An inequality written in one of the forms y <ax2 + bx + c,
y ≥ ax2 + bx + c, y ≤ ax2 + bx + c, or y > ax2 + bx + c is called a quadratic inequality.
Quadratic term: A term ax2 is the quadratic term in the equation f(x) = ax2 + bx + c
Examples of Quadratic Function
The following are few examples of quadratic functions.
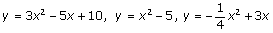
Video Examples: Quadratic Functions
Solved Example on Quadratic Function
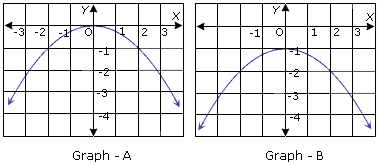
Ques: Graph the quadratic function y = - (1/4)x2.Indicate whether the parabola opens up or down.
Choices:
A. Graph-A; opens down
B. Graph-B; opens down
Correct Answer: A
Solution:
Step 1: Make a table of ordered pairs for the given function.
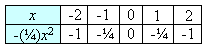
Step 2: Plot these points on the coordinate plane and connect the points with a smooth curve.
Step 3: The graph looks like the one below
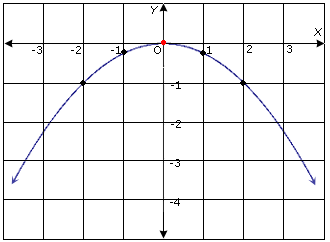
Step 4: It can be observed from the graph that the parabola opens down.
Step 5: The equation of the axis of symmetry is: x = 0
Step 6: The vertex is at (0, 0)
Step 7: The parabola opens down. So, the vertex is the maximum point.