Solved Examples and Worksheet for Net Figures made up of Rectangles and Triangles

Q1How many triangular faces are there in the pyramid?

A. 4
B. 5
C. 3
D. 6

Solutions
Share 
Step: 1
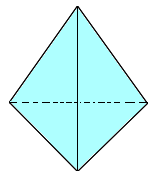
In the figure, the base of the pyramid is a triangle.
Step: 2
So, it is a triangular pyramid with 3 base edges.
Step: 3
The faces of the pyramid joining the base edge to the vertex are the triangular faces of the pyramid.
Step: 4
So, there are 4 triangular faces in the pyramid.
Correct Answer is :   4
Q2Find the number of rectangular faces in a decagonal prism.

A. 7
B. 9
C. 8
D. 10

Solutions
Share 
Step: 1
The base of a decagonal prism is a decagon.
Step: 2
The number of rectangular faces in a prism equals the number of sides of the base polygon.
Step: 3
Number of rectangular faces in a decagonal prism = Number of sides in a decagon =10
Step: 4
So, a decagonal prism will have 10 rectangular faces.
Correct Answer is :   10
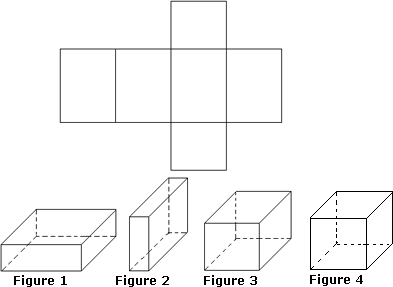
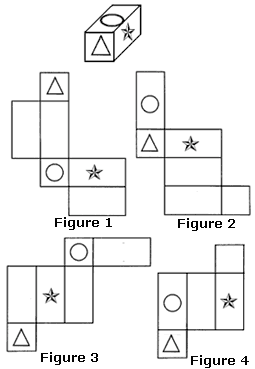
Q3Identify the rectangular prism that the net shown would fold into.



A. Figure 3
B. Figure 1
C. Figure 4
D. Figure 2

Solutions
Share 
Step: 1
A rectangular prism has two congruent rectangular bases and four rectangular side faces joining the two bases, where the opposite side faces are parallel and congruent.
Step: 2
When the given net is folded, it matches with Figure 3.
Step: 3
So, Figure 3 is the rectangular prism that the net shown would fold into.
Correct Answer is :   Figure 3
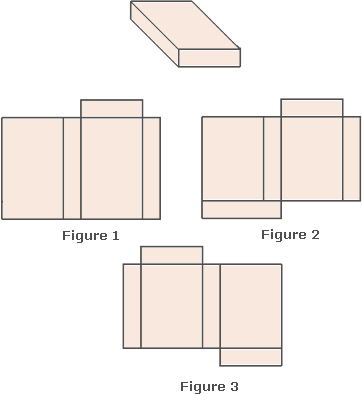
Q4Identify the net that represents the rectangular prism shown.

A. Figure 2
B. Figure 1
C. Figure 3
D. Figure 4

Solutions
Share 
Step: 1
The nets in Figure 1, Figure 3 cannot be folded into a rectangular prism as shown.
Step: 2
The net in Figure 2 can be folded into the rectangular prism as shown.
Step: 3
The net in Figure 4 has only 5 faces.
  [A rectangular prism has six faces in the form of rectangles or squares, with the opposite side faces being congruent and parallel.]
Step: 4
So, the net in Figure 2 represents the rectangular prism shown.
Correct Answer is :   Figure 2
Q5Which net represents the rectangular prism shown?


A. Figure 3
B. Figure 2
C. Figure 1
D. Figure 4

Solutions
Share 
Step: 1
The net in Figures 2, 3, and 4 cannot be folded into rectangular prism as shown.
Step: 2
So, the net in Figure 1 represents the rectangular prism shown.
Correct Answer is :   Figure 1
Q6Which of the nets can be folded to form a rectangular prism?


A. Figure 1
B. Figure 3
C. Figure 2

Solutions
Share 
Step: 1
A rectangular prism has six faces in the form of rectangles or squares, with the opposite side faces being congruent and parallel.
Step: 2
The nets in Figure 1 and Figure 2 cannot be folded into rectangular prisms as they have only 5 faces.
Step: 3
Figure 3 has six faces and its bases are in the form of squares.
Step: 4
So, Figure 3 can be folded to form a rectangular prism .
Correct Answer is :   Figure 3
Q7Identify the net for the rectangular prism.

A. Figure 2
B. Figure 3
C. Figure 1

Solutions
Share 
Step: 1
The net in Figure 1 has only 5 faces.
  [A rectangular prism has six faces in the form of rectangles or squares, with the opposite sides being congruent and parallel.]
Step: 2
The nets in Figure 2 has six faces but cannot be folded into a rectangular prism as shown.
Step: 3
The net in Figure 3 can be folded into a rectangular prism as shown.
Step: 4
So, Figure 3 represents the net for the rectangular prism.
Correct Answer is :   Figure 3
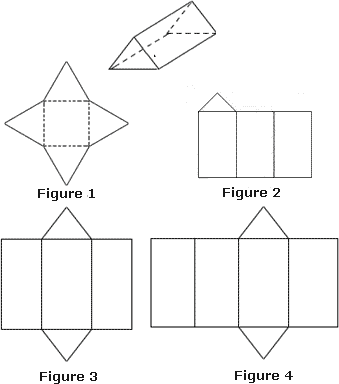
Q8Identify the net for the triangular prism shown.


A. Figure 1
B. Figure 2
C. Figure 4
D. Figure 3

Solutions
Share 
Step: 1
The triangular prism has 5 faces including the 2 triangular bases.
Step: 2
Among the given figures, Figure 3 has 2 triangular bases and 3 rectangular faces.
Step: 3
So, Figure 3 is the net for forming a triangular prism.
Correct Answer is :   Figure 3
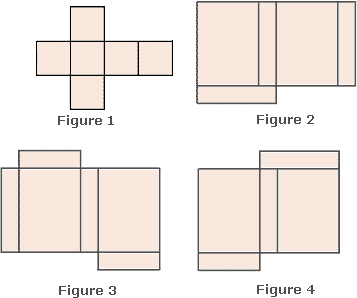
Q9Which of the nets can be folded up to form a cuboid?


A. Figure 1
B. Figure 4
C. Figure 3
D. Figure 2

Solutions
Share 
Step: 1
A solid whose bases are rectangles is called a cuboid.
Step: 2
Figure 1 can't folded up to form rectangular solids since it has square shape bases.
Step: 3
Figures 2 and 4 can't be folded up to form rectangular solids since they have only 5 faces.
Step: 4
Figure 3 has six faces and its bases are in rectangular shape.
Step: 5
So, Figure 3 can be folded into a cuboid.
Correct Answer is :   Figure 3
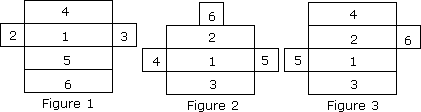
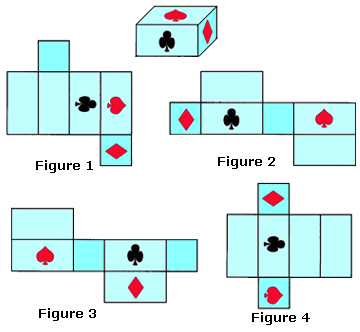
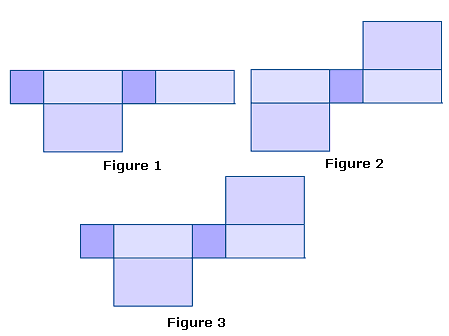
Q10Which of the nets can be folded to form a rectangular box ?


A. All figures
B. Figure 1 and Figure 3
C. Figure 1 only
D. Figure 3 only

Solutions
Share 
Step: 1
A rectangular box with the top has 6 faces. The opposite faces of the box are parallel and congruent.
Step: 2
If you fold the net shown in Figure 1, box 1 is the base, boxes 2, 3, 4 and 5 will form lateral faces and box 6 is placed in the top part. The figure looks like rectangular box.
Step: 3
Figure 2 has 3 rectangular and 3 square boxes.
Step: 4
If you fold the net shown in Figure 2, box 1 is the base, boxes 2, 3, 4 and 5 will form lateral faces and the box 6 is the top part. In the closed figure, the top is not covered fully.
Step: 5
So, figure 2 cannot form a rectangular box.
Step: 6
Figure 3 has 4 rectangular and 2 square boxes.
Step: 7
If you fold the net shown in Figure 3, box 1 is the base and the boxes 2, 3, 5 and 6 will form lateral faces and the box 4 is the top part, which is in the shape of a rectangular box.
Step: 8
Figure 1 and Figure 3 form a closed rectangular box with a top.
Correct Answer is :   Figure 1 and Figure 3

HighSchool Math