Solved Examples and Worksheet for Volume of Pyramids

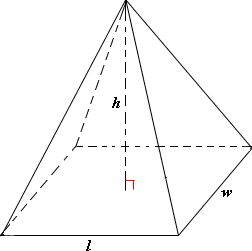
Q1What is the base area and volume of the rectangular pyramid, whose length, width, and height are 13.8 cm, 9.2 cm and 11.5 cm respectively?

A. 136.96 cm2 and 496.68cm3
B. 126.96 cm2 and 486.68 cm3
C. 126.96 cm2 and 1460.04 cm3
D. 146.96 cm2 and 506.68cm3

Solutions
Share 
Step: 1
The base area of the rectangular pyramid = length × width
Step: 2
= 13.8 × 9.2
  [Substitute the values.]
Step: 3
= 126.96 cm2
  [Multiply 13.8 by 9.2.]
Step: 4
The volume of a rectangular pyramid = (13) × base area × height
Step: 5
= (13) × 126.96 × 11.5
  [Substitute the values.]
Step: 6
= 1460.043
  [Multiply 126.96 by 11.5.]
Step: 7
= 486.68 cm3
  [Divide.]
Step: 8
The base area and volume of the rectangular pyramid are 126.96 cm2 and 486.68 cm3.
Correct Answer is :   126.96 cm2 and 486.68 cm3
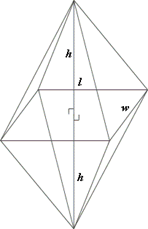
Q2If l = 5 cm, h = 4 cm and w = 3 cm, then find the volume of the figure shown.


A. 80 cm3
B. 40 cm3
C. 20 cm3
D. 60 cm3

Solutions
Share 
Step: 1
From the figure, the length, width and height of the rectangular pyramid are 5 cm, 4 cm and 3 cm respectively.
Step: 2
The base area of the rectangular pyramid = length × width
Step: 3
= 5 × 3
  [Substitute the values.]
Step: 4
= 15 cm2
  [Multiply.]
Step: 5
The volume of the rectangular pyramid = (13) × base area × height
Step: 6
= (13) × 15 × 4
  [Substitute the values.]
Step: 7
= 20 cm3
  [Simplify.]
Step: 8
The volume of the figure = 2 × volume of the rectangular pyramid
Step: 9
= 2 × 20
  [Substitute volume = 212.96]
Step: 10
= 40 cm3
  [Multiply.]
Step: 11
∴ The volume of the figure is 40 cm3.
Correct Answer is :   40 cm3
Q3The base of a pyramid is a right triangle and two sides containing the right angle are 6 ft and 6 ft. If height of the pyramid is 9 ft, then find the volume of the pyramid.
A. 54 ft3
B. 63 ft3
C. 49 ft3
D. 60 ft3

Solutions
Share 
Step: 1
Base of the pyramid = right triangle
Step: 2
Base area of the pyramid = area of right triangle = 12× base × height = 12× 6 × 6 = 18 ft2.
Step: 3
Volume of the pyramid = 13× base area × height
  [Formula.]
Step: 4
= 13 × 18 × 9
  [Substitute the values.]
Step: 5
= 54
  [Simplify.]
Step: 6
Volume of the pyramid = 54 ft3.
Correct Answer is :   54 ft3
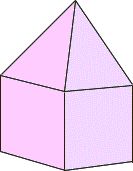
Q4A pyramid is placed on a cube of 12 cm edge as shown in the figure such that the total volume of the solid formed is 2160 cm3. What is the height of the pyramid?


A. 15 cm
B. 12 cm
C. 9 cm
D. 21 cm

Solutions
Share 
Step: 1
Height of a cube = length of each edge of a cube = 12 cm
Step: 2
Total height of the figure = height of pyramid + height of cube
15 = height of the pyramid + 12
  [Substitute the values.]
Step: 3
Height of the pyramid = 3 cm
  [Subtract 12 from each side.]
Step: 4
Volume of the cube = s3 = 123 = 1728 cm3.
Step: 5
Volume of the pyramid = 13 × base area × height
  [Formula.]
Step: 6
= 13 × 122 × 3
  [Substitute the values.]
Step: 7
= 144
  [Simplify.]
Step: 8
Volume of the pyramid = 144 cm3
  [Simplify.]
Step: 9
Volume of the figure = volume of the cube + volume of the pyramid
= 1728 + 144 = 1872
  [Substitute the values and add.]
Step: 10
Volume of the figure = 1872 cm3.
Correct Answer is :   9 cm
Q5A tent is in the form of a square pyramid with a base length of 21 m. The slant height of the pyramid is 16 m. If the rate of making the tent is $60 per cubicmeter, then what is the cost of making the tent?

A. $106457.40
B. $106485.40
C. $106507.40
D. $106496.40

Solutions
Share 
Step: 1
Base length = 21 m
  [Given.]
Step: 2
Slant height = 16 m.
Step: 3
Height of the tent = 162-(212)2 = 12.07 m
  [Height of tent = l2-a24.]
Step: 4
Volume of the tent = 13× 212 × 12.07 = 1774.29 m3
  [Volume of the pyramid = 13a2h.]
Step: 5
Rate of making = $60 per m3
  [Given.]
Step: 6
Cost of making the tent = Volume of the tent × Rate of making
  [Formula.]
Step: 7
Cost of making the tent = 1774.29 × 60 = $106457.40
  [Substitute in step 6 and simplify.]
Correct Answer is :   $106457.40
Q6A toy is in the form a square pyramid. The edge of the lateral side measures 7cm. The height of the toy is 3 cm. How many of such toys can be moulded by melting a metallic piece of 2 m × 2 m × 5 m ? Approximate your answer.

A. 250376
B. 233833
C. 260252
D. 238031

Solutions
Share 
Step: 1
Number of toys = Volume of the metallic piece Volume of one pyramid
  [Formula.]
Step: 2
Volume of the metallic piece = 2 × 2 × 5 m3 = 20 m³
  [According to the data.]
Step: 3
Height of the pyramid = 3 cm.
  [Given.]
Step: 4
Length of lateral edge = 7 cm.
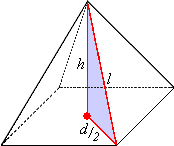
  [Given.]

Step: 5
Lateral edge, height and half of the diagonal forms a right triangle.
  [From the figure.]
Step: 6
d2= 7² - 3² = 6.32.
  [d2= Lateral side² - h².]
Step: 7
d = 2 × 6.32 = 12.64
  [Multiply each side by 2.]
Step: 8
Volume of one pyramid = 13× 12.64²2 × 3 = 79.88 cm3
  [Volume of pyramid = 13× base area × height.]
Step: 9
Number of toys = 20×100×100×10079.88= 250376 toys (approximately)
  [Substitute in step 1 and simplify.]
Correct Answer is :   250376
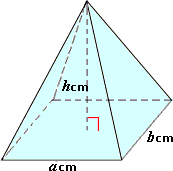
Q7Find the volume of the rectangular pyramid. [a = 7, b = 6 and h = 12.]


A. 504 cm3
B. 75 cm3
C. 168 cm3
D. 168 cm2

Solutions
Share 
Step: 1
From the figure, the length, width and height of the rectangular pyramid are 7 cm, 6 cm, and 12 cm, respectively.
Step: 2
Volume of a rectangular pyramid = (13) × length × width × height
Step: 3
= (13) × 7 × 6 × 12
  [Substitute the values.]
Step: 4
= 5043 cm3
Step: 5
= 168 cm3
  [Simplify.]
Step: 6
The volume of the rectangular pyramid is 168 cm3.
Correct Answer is :   168 cm3
Q8The formula for the volume of a rectangular pyramid is V = (13)lwh. Find the length l of the pyramid.

A. V3wh
B. 3Vwh
C. wh3V
D. 3whV

Solutions
Share 
Step: 1
V = (13)lwh
  [Given.]
Step: 2
3V = 3 × 13× lwh.
  [Multiply by 3 on each side.]
Step: 3
3V = lwh
  [Simplify.]
Step: 4
3Vwh = lwhwh
  [Divide each side by wh.]
Step: 5
l = 3Vwh
  [Simplify.]
Step: 6
Therefore, the length of the rectangular pyramid is 3Vwh.
Correct Answer is :   3Vwh
Q9The formula for the volume of a rectangular pyramid is V = (13)lwh.. Find the width (w) of the pyramid.

A. 3Vlh
B. lh3V
C. V3lh
D. 3lhv

Solutions
Share 
Step: 1
V = (13)lwh
  [Given.]
Step: 2
3V = 3 × 13× lwh
  [Multiply by 3 on each side.]
Step: 3
3V = lwh
  [Simplify.]
Step: 4
3Vlh = lwhlh
  [Divide each side by lh.]
Step: 5
3Vlh = w
  [Simplify.]
Step: 6
Therefore, the width of the rectangular pyramid is 3Vlh.
Correct Answer is :   3Vlh
Q10What is the height of a rectangular pyramid, whose base area is 108 cm2 and volume is 396 cm3?
A. 11 cm
B. 7 cm
C. 9 cm
D. 12 cm

Solutions
Share 
Step: 1
The volume of the rectangular pyramid = 13× base area × height
  [Volume formula.]
Step: 2
The height of the rectangular pyramid = 3 × volumebase area.
Step: 3
= 3 × 396108
  [Substitute.]
Step: 4
= 3 × 113 = 11
  [Simplify.]
Step: 5
Therefore, the height of the rectangular pyramid is 11 cm.
Correct Answer is :   11 cm

HighSchool Math