Solved Examples and Worksheet for Volume of Cones

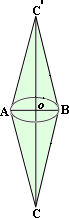
Q1Find the volume of the figure shown, if AB = 8 ft and CO = C′O = 18 ft.


A. 96π ft3
B. 94π ft3
C. 190π ft3
D. 192π ft3

Solutions
Share 
Step: 1
From the figure, the base diameter of each cone, d = AB = 8 ft
and the height of each cone, h = CO = 18 ft.
Step: 2
The base radius of the cone, r = diameter2
= 82
  [Substitute diameter = 8 ft.]
Step: 3
= 4 ft
  
Step: 4
Volume of each cone, V = 13πr2h
  [Formula.]
Step: 5
= 13 × π × 42 × 18
  [Substitute r = 4 and h = 18.]
Step: 6
= 96π ft3
  [Simplify.]
Step: 7
The volume of the figure = 2 × V
  [Since the figure contains two identical cones.]
Step: 8
= 2 × 96π ft3
  [Substitute, V = 96π ft3.]
Step: 9
= 192π ft3
  
Step: 10
The volume of the figure is 192π ft3.
Correct Answer is :   192π ft3
Q2Find the height of the cone whose volume is 480π cm3 and base radius is 12 cm.
A. 13 cm
B. 20 cm
C. 30 cm
D. 10 cm

Solutions
Share 
Step: 1
Let h be the height of the cone and r be the base radius of the cone.
Step: 2
Volume of the cone, v = (13)πr2h
  [Volume formula.]
Step: 3
The height of the cone, h = 3vπr2
Step: 4
= 3 × 480ππ×122
  [Substitute v = 480π and r = 12.]
Step: 5
= 10 cm
  [Simplify.]
Step: 6
The height of the cone is 10 cm.
Correct Answer is :   10 cm
Q3What is the base radius of a cone, whose volume is 48π ft3 and height is 4 ft?
A. 8 ft
B. 5 ft
C. 9 ft
D. 6 ft

Solutions
Share 
Step: 1
Let r be the radius of the cone.
Step: 2
Volume of the cone, V = (13)πr2h
  [Formula.]
Step: 3
r = 3Vπh
  [Rewrite the formula.]
Step: 4
= 3 × 48ππ × 4
  [Substitute V = 48π and h = 4.]
Step: 5
= 6 ft
  [Simplify.]
Step: 6
The base radius of the cone is 6 ft.
Correct Answer is :   6 ft
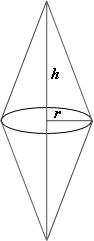
Q4What is the volume of the figure shown?[Given r = 7.5 cm, h = 12.5 cm.]


A. 248.37π cm 3
B. 298.37π cm3
C. 218.37π cm3
D. 468.74π cm3

Solutions
Share 
Step: 1
From the figure, the base radius of each cone, r = 7.5 cm
and the height of each cone, h = 12.5 cm
Step: 2
Volume of each cone, V = 13πr2h
  [Volume formula.]
Step: 3
= 13 × π × (7.5)2 × 12.5
  [Substitute r = 7.5 and h = 12.5.]
Step: 4
= 234.37π cm3
  [Simplify.]
Step: 5
The volume of the figure = 2 × V
  [The figure contains two identical cones.]
Step: 6
= 2 × 234.37π
  [Substitute V = 234.37π.]
Step: 7
= 468.74π cm3
Step: 8
The volume of the figure is 468.74π cm3.
Correct Answer is :   468.74π cm3
Q5Find the volume of the cone in the figure. [Given r = 4.6 cm, h = 6.9 cm.]


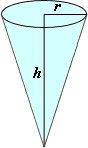
A. 58.67π cm3
B. 73π cm3
C. 48.67π cm3
D. 32.45π cm3

Solutions
Share 
Step: 1
From the figure, base radius of the cone, r = 4.6 cm and height, h = 6.9 cm
Step: 2
Volume of the cone = 13πr2h
  [Formula.]
Step: 3
= 13 × π × 4.62 × 6.9
  [Substitute base radius, r = 4.6 cm and height, h = 6.9 cm.]
Step: 4
= 146π3
  [Divide numerator and denominator by 3.]
Step: 5
= 48.67π
  [Simplify.]
Step: 6
The volume of the cone is 48.67π cm3.
Correct Answer is :   48.67π cm3
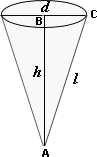
Q6What is the volume of the cone whose diameter(d) is 13.8 cm and slant height(l) is 11.5 cm?

A. 292π cm3
B. 156π cm3
C. 146 cm3
D. 146π cm3

Solutions
Share 
Step: 1
The base radius of the cone, r = diameter2 = 13.82 = 6.9 cm
  [Since, the diameter of the cone is 13.8 cm.]
Step: 2
From the figure, AB2 + BC2 = AC2
  [Pythagorean theorem.]
Step: 3
h2 + (6.9)2 = (11.5)2
  [Substitute AB = h, BC = 6.9 cm, and AC = 11.5 cm.]
Step: 4
47.6 + h2 = 132.3
  [Evaluate powers.]
Step: 5
h2 = 132.3 - 47.6
  [Subtract 47.6 from both sides.]
Step: 6
h2 = 84.7
Step: 7
h = 84.7 = 9.2
  [Take square root on both sides.]
Step: 8
The height of the cone is 9.2 cm.
Step: 9
The volume of the cone = 13πr2h
  [Volume formula.]
Step: 10
= 13 × π × (6.9)2 × 9.2
  [Substitute r = 6.9 and h = 9.2.]
Step: 11
= 146π cm3
  [Simplify the expression.]
Step: 12
The volume of the cone is 146π cm3.
Correct Answer is :   146π cm3
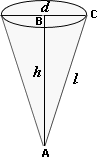
Q7What is the volume of the cone whose diameter is 18 ft and slant height is 15 ft?


A. 81π ft3
B. 324π ft3
C. 972π ft3
D. 111π ft3

Solutions
Share 
Step: 1
The base radius of the cone, r = diameter2
= 182= 9 ft
  [Since the diameter of the cone is 18 ft.]
Step: 2
From the figure, AB2 + BC2 = AC2
  [Pythagorean theorem.]
Step: 3
h2 + 92 = 152
  [Substitute AB = h, BC = 9 ft, and AC = 15 ft.]
Step: 4
h2 + 81 = 225
  [Evaluate powers.]
Step: 5
h2 = 225 - 81
  [Subtract 81 from both sides.]
Step: 6
h2 = 144
  [Subtract.]
Step: 7
h = 144
h = 12
  [Take square root on both sides.]
Step: 8
The height of the cone is 12 ft.
Step: 9
The volume of the cone = 13πr2h
  [Volume formula.]
Step: 10
= 13× π × 92 × 12
  [Substitute r = 9 and h = 12.]
Step: 11
= 324π ft3
  [Simplify the expression.]
Step: 12
The volume of the cone is 324π ft3.
Correct Answer is :   324π ft3
Q8The radius of the base of a right circular cone is 3r mm and its height is equal to the radius of the base. Find its volume in mm3.
A. 4πr3mm3
B. 11πr3mm3
C. 9πr3 mm3
D. 14πr3 mm3

Solutions
Share 
Step: 1
Height of a cone = base radius of the cone = 3r mm.
Step: 2
Volume of a cone = 13πr2h
  [Formula.]
Step: 3
= 13 × π × (3r)2 × 3r
  [Substitute the values.]
Step: 4
= 9πr3
  [Simplify.]
Step: 5
The volume of the right circular cone = 9πr3 mm3.
Correct Answer is :   9πr3 mm3
Q9Base radius of a cone is 4 in. and its height is 7.5 in. If the height and the radius of the cone are doubled, then find the volume of the new cone.
A. 502.4 in.3
B. 1004.8 in.3
C. 334.93 in.3
D. 3014.4 in.3

Solutions
Share 
Step: 1
Base radius of the new cone = 2 × radius of the initial cone = 2 × 4 = 8 in.
  [Since base radius of new cone is double the radius of initial cone.]
Step: 2
Height of the new cone = 2 × height of the initial cone = 2 × 7.5 = 15 in.
  [Since height of new cone is double the height of initial cone.]
Step: 3
Volume of cone = 13πr2h
  [Formula.]
Step: 4
Volume of new cone = 13× π × 82 × 15
= 1004.8
  [Substitute the values in the formula and simplify.]
Step: 5
Volume of the new cone is 1004.8 in.3.
Correct Answer is :   1004.8 in.3
Q10What is the volume of a cone, if its radius is 9 cm and its curved surface area is 423.9 cm2? (Round the answer to the nearest whole number.)

A. 1014 cm3
B. 1022 cm3
C. 1017 cm3
D. 1025 cm3

Solutions
Share 
Step: 1
Curved surface area of cone = πrl
  [Formula.]
Step: 2
πrl = 423.9
  [Since curved surface area of cone is 423.9 cm2.]
Step: 3
3.14 × 9 × l = 423.9
  [Substitute the values of π and r.]
Step: 4
l = 15
  [Simplify.]
Step: 5
Slant height of the cone (l) = 15.
Step: 6
Height of cone2 = slant height of cone2 - radius2.
Step: 7
Height of cone2 = 152 - 92
  [Substitute the values.]
Step: 8
Height of the cone = 12 cm
  [Take the square root of each side.]
Step: 9
Volume of cone = 13 πr2h
  [Formula.]
Step: 10
= 13× 3.14 × 92 × 12
  [Substitute the values.]
Step: 11
= 1017.36
  [Simplify.]
Step: 12
≈ 1017
  [Round the answer to the nearest whole number.]
Step: 13
Volume of the cone = 1017 cm3.
Correct Answer is :   1017 cm3
Q11The height of a right circular cone is 12 cm. If its volume is 1024π cm3, what is the slant height of the cone?

A. 20 cm
B. 16 cm
C. 29 cm
D. 25 cm

Solutions
Share 
Step: 1
Volume of a cone = 13πr2h
  [Formula.]
Step: 2
1024π = 13 × π × r2 × 12
  [Substitute the values.]
Step: 3
r2 = 256
  [Simplify.]
Step: 4
Slant height of cone (l) = r2+h2
Step: 5
= (256+122)
  [Substitute the values.]
Step: 6
= 400 = 20
  [Simplify.]
Step: 7
Slant height of the cone = 20 cm.
Correct Answer is :   20 cm
Q12The circumference of the base of a cone of height 21 in. is 132 in. Find the volume of the cone. (Use π = 227)
A. 9697.2 in.3
B. 9706.8 in.3
C. 9702 in.3
D. 9716.8 in.3

Solutions
Share 
Step: 1
Circumference of the base of a cone = 2πr
  [Formula.]
Step: 2
2πr = 132 in.
  [Since circumference of a cone is 132 in.]
Step: 3
2 × 227 × r = 132
  
Step: 4
r = 21 in.
  [Simplify.]
Step: 5
Volume of the cone = 13πr2h
  [Formula.]
Step: 6
= 13 × 227 × 212 × 21
  [Substitute the values.]
Step: 7
= 9702
  [Simplify.]
Step: 8
Volume of the cone = 9702 in.3
Correct Answer is :   9702 in.3
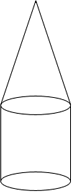
Q13A tent is in the shape of a cylinder with a conical top. The radius of the base of the tent is 8 m. The height of the cylindrical part is 15 m and that of the conical part is 24 m. Find the volume of air that occupies the tent. (Round the answer to one decimal place.)

A. 47 m3
B. 4622.1 m3
C. 4607.1 m3
D. 2880 m3

Solutions
Share 
Step: 1
Volume of cylindrical part = πr2h
  [Formula.]
Step: 2
= 3.14 × 82 × 15
  [Substitute the values.]
Step: 3
= 3014.40
  [Simplify.]
Step: 4
Volume of the cylindrical part = 3014.40 m3.
Step: 5
Volume of Conical part = 13πr2h
  [Formula.]
Step: 6
= 13 × 3.14 × 82 × 24
  [Substitute the values.]
Step: 7
= 1607.68
  [Simplify.]
Step: 8
Volume of the cone = 1607.68 m3.
Step: 9
Volume of air that occupies the tent = volume of cylindrical part + volume of conical part
= (1607.68 + 3014.40) m3 = 4622.08 m3
  
Step: 10
≈ 4622.1 m3
  [Round the answer to one decimal place.]
Step: 11
Volume of air that occupies the tent = 4622.1 m3.
Correct Answer is :   4622.1 m3
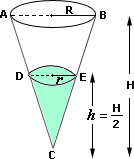
Q14The height of 3 ounces of liquid in a conical cup is half of the height of the cup. How many ounces of the liquid will be required to fill the entire conical cup?


A. 24 ounces
B. 6 ounces
C. 12 ounces
D. 29 ounces

Solutions
Share 
Step: 1
Volume of the cup, V = 13π R2 H
  [Volume of the cone = 13π r2 h.]
Step: 2
Volume of the part of the conical cup containing liquid in it, v = 13 πr2h
Step: 3
Consider ΔABC and ΔDEC, Rr=Hh
  [As ΔABC and ΔDEC are similar triangles.]
Step: 4
Rr=HH2
  [Given, h = H2.]
Step: 5
Rr=2
  [Simplify.]
Step: 6
Vv = volume of the total cupvolume of the part of the cup containing liquid
Step: 7
Vv=13πR2H13πr2h
  [Formula.]
Step: 8
V3=(Rr)2×HH2
  [Volume of the liquid = 3 ounces.]
Step: 9
V3=4×2
  [From steps 4 and 5.]
Step: 10
V = 3 × 4 × 2
  [Multiply with 3 on both sides.]
Step: 11
V = 24 ounces
  [Simplify.]
Step: 12
So, the volume of the liquid required to fill the entire conical cup = 24 ounces
Correct Answer is :   24 ounces
Q15Base radius of a cone is 6 in. and its height is 22.50 in. If the height and the radius of the cone are doubled, then find the volume of the new cone.[Use π = 3.]
A. 19440 in.3
B. 1656 in.3
C. 3240 in.3
D. 6480 in.3

Solutions
Share 
Step: 1
Base radius of the new cone = 2 × radius of the initial cone = 2 × 6 = 12 in.
  [Since base radius of new cone is double the radius of initial cone.]
Step: 2
Height of the new cone = 2 × height of the initial cone = 2 × 22.50 = 45 in.
  [Since height of new cone is double the height of initial cone.]
Step: 3
Volume of cone = 13πr2h
  [Formula.]
Step: 4
Volume of new cone = 13× 3 × 122 × 45
= 6480
  [Substitute the values in the formula and simplify.]
Step: 5
Volume of the new cone is 6480 in.3.
Correct Answer is :   6480 in.3

HighSchool Math