Writing Linear Equations using Rate of Change for a Situation or a Table-Algebra1-Solved Examples

Solved Examples and Worksheet for Writing Linear Equations using Rate of Change for a Situation or a Table

Q1Holly earns $70 everyday by working for 7 hours. She gets $20 for every extra hour worked. The table shows the relationship between the number of extra hours and Holly's total earnings per day. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Extra Hours (x)	1	2	3
Total Earnings (y)	90	110	130

A. x = 20y + 70
B. y = 20x - 70
C. y = 20x + 70
D. x = 20y - 70

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of extra hours and the output variable y gives the total earnings of John per day.

Step: 3

Change in output values = 20

Step: 4

Change in input values = 1

Step: 5

Rate of change = chnage in output valueschange in input values = 201 = 20

Step: 6

Working backwards with the values in the table, we get (0, 70).

Step: 7

So, the linear equation that satisfies the table is y = 20x + 70.

[Substitute rate of change and y - intercept values.]

Correct Answer is : y = 20x + 70

Q2The minimum charges of a DVD Player borrowed on rent is $8. The charges increase by $3 for each day. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Days (x)	1	2	3	4
Cost in Dollars (y)	11	14	17	20

A. x = 3y + 8
B. y = 3x - 8
C. y =3 x + 8
D. x = 3y - 8

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of days and the output variable y is the cost.

Step: 3

Change in output values = 3

Step: 4

Change in input values = 1

Step: 5

Rate of change = change in output valueschange in input values = 31 = 3

Step: 6

Working backwards with the values in the table, we get (0, 8).

Step: 7

So, the linear equation that satisfies the table is y = 3x + 8.

[Substitute rate of change and y - intercept values.]

Correct Answer is : y =3 x + 8

Q3John is working in an electronic store. He earns $140 per day for the 5 products he sells. He gets $30 for every additional product he sells. The table shows the relationship between the number of additional products sold and John's total earnings per day. Use the rate of change to identify a linear equation for the data shown in the table.

Number of additional products (x)	1	2	3
Total Earnings (y)	170	200	230

A. x = 30y + 140
B. y = 30x + 140
C. y = 30x + 170
D. x = 30y - 170

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of extra products and the output variable y gives the total earnings of John per day.

Step: 3

Change in output values = 30

Step: 4

Change in input values = 1

Step: 5

Rate of change = change in output valueschange in input values = 301 = 30

Step: 6

Working backwards with the values in the table, we get (0, 140).

Step: 7

So, the linear equation that satisfies the table is y = 30x + 140.

[Substitute rate of change and y - intercept values.]

Correct Answer is : y = 30x + 140

Q4Paula earns a salary of $180 per month plus 7% commission on her sales.The table shows the relationship between her sales and earnings. Use the rate of change to identify a linear equation for the data shown in the table.

Sales Worth (x)	100	200	300	400
Salary in Dollars (y)	187	194	201	208

A. y = 0.07x + 187
B. x = 0.07y + 180
C. y = 0.07x + 180
D. x = 0.07y + 187

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the sales worth and the output variable y is the salary.

Step: 3

Change in output values = 7

Step: 4

Change in input values = 100

Step: 5

Rate of change = chnage in output valueschange in input values = 7100 = 0.07

Step: 6

Working backwards with the values in the table, we get (0, 180).

Step: 7

So, the linear equation that satisfies the table is y = 0.07x + 180.

[Substitute rate of change and y - intercept values.]

Correct Answer is : y = 0.07x + 180

Q5The table shows the relationship between the number of hours Nick drives and the distance covered on his journey. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Hours (x)	1	2	3	4
Distance in miles (y)	51	72	93	114

A. y = 21x + 51
B. x = 21y - 51
C. x = 21y + 30
D. y = 21x + 30

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of hours and the output variable y is Nick's earnings.

Step: 3

Change in output values = 21

Step: 4

Change in input values = 1

Step: 5

Rate of change = change in output valueschange in input values = 211 = 21

Step: 6

Working backwards with the values in the table, we get (0, 30).

Step: 7

So, the linear equation that satisfies the table is y = 21x + 30.

Correct Answer is : y = 21x + 30

Q6Ed borrows a CD for 16 cents. For each day he needs to pay 10 cents extra. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Days (x)	1	2	3	4
Cost in Cents (y)	26	36	46	56

A. x = 10y - 26
B. y = 10x + 26
C. x = 10y + 16
D. y = 10x + 16

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of days and the output variable y is the cost.

Step: 3

Change in output values = 10

Step: 4

Change in input values = 1

Step: 5

Rate of change = change in output valueschange in input values = 101 = 10

Step: 6

Working backwards with the values in the table, we get (0, 16).

Step: 7

So, the linear equation that satisfies the table is y = 10x + 16.

[Substitute rate of change and y - intercept values.]

Correct Answer is : y = 10x + 16

Q7The minimum charges of a book borrowed on rent is $5. The charges increase by $2 for each day. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Days (x)	1	2	3	4
Cost in Dollars (y)	7	9	11	13

A. x = 2y - 5
B. y = x2 + 5
C. y = 2x + 5
D. x = y2 + 5

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of days and the output variable y is the cost.

Step: 3

Change in output values = 2

Step: 4

Change in input values = 1

Step: 5

Rate of change = change in output valueschange in input values = 21 = 2

Step: 6

Working backwards with the values in the table, we get (0, 5).

Step: 7

So, the linear equation that satisfies the table is y = 2x + 5

[Substitute rate of change and y - intercept values.]

Correct Answer is : y = 2x + 5

Q8The table shows the relationship between a waiter′s earnings (in $) and the number of hours he works overtime in a restaurant. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Hours (x)	1	2	3	4
Earnings in Dollars (y)	31	34	37	40

A. y = 3x + 28
B. y = x3 - 28
C. y = 3x + 31
D. y = x3 + 28

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of hours and the output variable y is the waiter's earnings.

Step: 3

Change in output values = 3

Step: 4

Change in input values = 1

Step: 5

Rate of change = chnage in output valueschange in input values = 31 = 3

Step: 6

Working backwards with the values in the table, we get (0, 28).

Step: 7

So, the linear equation that satisfies the table is y = 3x + 28.

Correct Answer is : y = 3x + 28

Q9Jim borrows a CD player for 38 cents. For each day he needs to pay 6 cents extra. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Days (x)	1	2	3	4
Cost in Cents (y)	44	50	56	62

A. y = 6x + 44
B. y = 6x + 38
C. x = 6y + 38
D. y = 6x - 38

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of days and the output variable y is the cost.

Step: 3

Change in output values = 6

Step: 4

Change in input values = 1

Step: 5

Rate of change = change in output valueschange in input values = 61 = 6

Step: 6

Working backwards with the values in the table, we get (0, 38).

Step: 7

So, the linear equation that satisfies the table is y = 6x + 38.

[Substitute rate of change and y - intercept values.]

Correct Answer is : y = 6x + 38

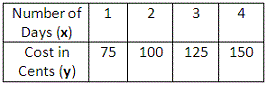
Q10Gary borrows a DVD player for 50 cents. For each day he needs to pay 25 cents extra. Use the rate of change to identify a linear equation for the data shown in the table.

A. y = 0.25x + 0.5
B. y = 2.5x + 5
C. x = 0.25y + 0.5
D. y = 25x + 50

Solutions

Step: 1

Linear equation in intercept form is y = a + bx, where b is the rate of change and a is the y - intercept.

Step: 2

The input variable x is the number of days and the output variable y is the cost.

Step: 3

Change in output values = 25

Step: 4

Change in input values = 1

Step: 5

Rate of change = Change in output valuesChange in input values = 251 = 25

Step: 6

Working backwards with the values in the table, we get (0, 50). So, the y -intercept is 50.

Step: 7

So, the linear equation that satisfies the table is y = 25x + 50.

Correct Answer is : y = 25x + 50

Solved Examples and Worksheet for Writing Linear Equations using Rate of Change for a Situation or a Table

Related Worksheet

Related Topic

HighSchool Math