Solved Examples and Worksheet for Linear Programming Problems

Q1If the cost of a tape is $19 and the cost of a CD is $26, write the objective function for the cost(C) of c tapes and x CDs .

A. C = 45 + c + x
B. C = 19c + 26x
C. C = 494cx
D. C = 26c + 19x

Solutions
Share 
Step: 1
The cost of each tape is $19 and the cost of each CD is $26.
Step: 2
The cost C of c tapes and x CDs is C = 19c + 26x, which is the objective function for the cost.
Correct Answer is :   C = 19c + 26x
Q2A manufacturer makes two models A and B of a product, each to be processed by two machines. To complete one unit of model A, machines I and II must work 1 hour and 2 hours respectively. To complete one unit of model B, machines I and II must work 4 hours and 2 hours respectively. Machine I cannot be operated more than 8 hours in a day and machine II cannot be operated more than 10 hours per day. If the profits on models A and B per unit are $400 and $480, then how many units of each model should the manufacturer produce per day to maximize his profit?

A. 2 of A, 4 of B
B. 4 of A, 1 of B
C. 1 of A, 4 of B
D. 4 of A, 2 of B

Solutions
Share 
Step: 1
Let the number of units of models A and B to be made per day be x and y.
Step: 2
The objective function is P = 400x + 480y.
  [The manufacturer wants to maximize the profit P.]
Step: 3
To make x and y units of models A and B, machine I should be used for 1(x) + 4(y) hours. But one cannot use machine I for more than 8 hours per day, we have x + 4y ≤8.
Step: 4
To make x and y units of models A and B, machine II should be used for 2(x) + 2(y) hours. But one cannot use machine II for more than 10 hours per day, we have 2x + 2y ≤10 or x + y ≤ 5
Step: 5
x ≥ 0, y ≥ 0
  [As x , y are number of units.]
Step: 6
The feasible region determined by the above constraints is shown.
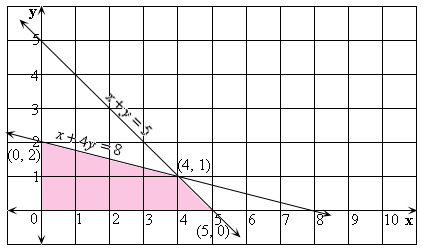
Step: 7
From the figure the vertices are (0, 0),(5, 0), (4, 1), (0, 2).
Step: 8
At (0, 0), P= 400(0) + 480(0) = 0
  [Substitute the values.]
Step: 9
At (5, 0), P = 400(5) + 80(0) = 2000
  [Substitute the values.]
Step: 10
At (4, 1), P = 400(4) + 480(1) = 2080
  [Substitute the values.]
Step: 11
At (0, 2), P = 400(0) + 480(2) = 960
  [Substitute the values.]
Step: 12
So, the maximum profit can be obtained by making 4 units of model A and 1 unit of model B.
Correct Answer is :   4 of A, 1 of B
Q3A factory produces two types of toys A and B with the help of two machines I and II. The two machines I and II can not be used for not more than 112 hours each to manufacture the toys. The toy A requires 1 minute of machine I and 2 minutes of II, where as a toy B takes 3 minutes of I and 1 minute of II. The profit for A is $70 and for B $60. How many of each type of toys are to be produced to give the maximum profit?

A. 36 toys of A, 18 toys of B
B. 80 toys of A, 70 toys of B
C. 45 toys of A, 30 toys of B
D. 60 toys of A, 10 toys of B

Solutions
Share 
Step: 1
Let the number of toys A and B to be made be x and y respectively.
Step: 2
The objective function is the profit P = 70x + 60y.
Step: 3
To make x number of toys A and y number of toys B, machine I should be used for 1(x) + 3(y) minutes. One cannot use the machine I for more than 112 hours, so we have x + 3y ≤ 90
  [ 112 hour = 90 minutes.]
Step: 4
To make x number of toys A and y number of toys B, the machine II should be used for 2(x) + 1(y) minutes. One cannot use the machine y for more than 112 hours, so we have 2x + y ≤ 90
  [112 hour = 90 minutes.]
Step: 5
x ≥ 0, y ≥ 0
  [x , y are number of toys.]
Step: 6
The feasible region determined by the above constraints is shown.
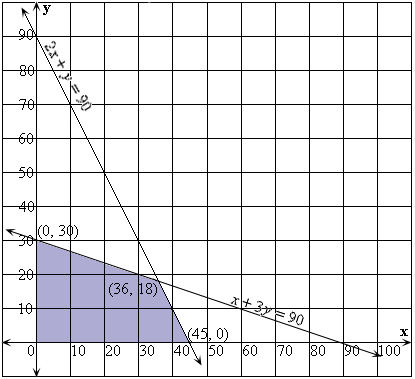
Step: 7
From the figure the vertices are (0, 0), (45, 0), (36, 18) and (0, 30).
Step: 8
At (0, 0), P = 70(0) + 60(0) = 0.
  [Substitute the values.]
Step: 9
At (45, 0), P = 70(45) + 60(0) = 3150.
  [Substitute the values.]
Step: 10
At (36, 18), P = 70(36) + 60(18) = 3600.
  [Substitute the values.]
Step: 11
At (0, 30), P = 70(0) + 60(30) = 1800.
  [Substitute the values.]
Step: 12
So, the maximum profit can be obtained by making 36 toys of A and 18 toys of B.
Correct Answer is :   36 toys of A, 18 toys of B
Q4A furniture dealer trades in two items: tables and chairs. He invests $60,000 in buying tables and chairs. He has a storage capacity for 600 pieces. A table costs him $120 and a chair $40. He can sell a table for a profit of $14 and a chair for a profit of $10. How should he invest his money in order to make maximum profit?

A. 450 tables, 150 chairs
B. 450 tables, 300 chairs
C. 300 tables, 150 chairs
D. 450 tables, 200 chairs

Solutions
Share 
Step: 1
Let the number of tables and chairs to be purchased be x and y.
Step: 2
P = 14x + 10y
  [Objective function is profit, P, profit for a table is $14 and a chair is $10.]
Step: 3
The dealer can invest $60,000 we have 120x + 40y ≤ 60,000 or 3x + y ≤ 1,500
  [Cost of table is $120, cost of chair is $40.]
Step: 4
x + y ≤ 600
  [The storage capacity is for 600 pieces.]
Step: 5
x ≥ 0, y ≥ 0
  [x , y are the number of tables and chairs.]
Step: 6
The feasible region determined by the above constraints is shown.
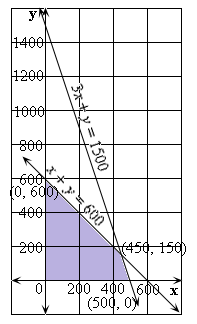
Step: 7
From the graph the vertices are (0, 0), (500, 0), (450, 150) and (0, 600)
Step: 8
At (0, 0), P = 14(0) + 10(0) = 0
  [Substitute the values.]
Step: 9
At (500, 0), P = 14(500) + 10(0) = 7000
  [Substitute the values.]
Step: 10
At (450, 150), P = 14(450) + 10(150) = 7800
  [Substitute the values.]
Step: 11
At (0, 600), P = 14(0) + 10(600) = 6000
  [Substitute the values.]
Step: 12
So, the maximum profit can be obtained by purchasing 450 tables and 150 chairs.
Correct Answer is :   450 tables, 150 chairs
Q5Tony can afford to buy 20 blackberries and 19 apricots. He wants at least 17 blackberries and at least 14 apricots. a represents the number of blackberries, and c represents the number of apricots that Tony buys. Which of the following systems of inequalities models this situation?
A. a ≤ 20, c ≤ 19, a ≥ 17, c ≥ 14
B. a ≤ 17, c ≤ 14, a ≥ 20, c ≥ 19
C. a ≥ 20, c ≥ 19, a ≥ 17, c ≥ 14
D. a ≤ 20, c ≤ 19, a ≤ 17, c ≤ 14

Solutions
Share 
Step: 1
a represents the number of blackberries and c represents the number of apricots that Tony buys.
Step: 2
The maximum number of blackberries that can be bought is 20. So, a ≤ 20.
Step: 3
The maximum number of apricots that can be bought is 19. So, c ≤ 19.
Step: 4
The minimum number of blackberries to be bought is 17. So, a ≥ 17.
Step: 5
The minimum number of apricots to be bought is 14. So, c ≥ 14.
Step: 6
So, the system of inequalities that models the given situation is:
a ≤ 20, c ≤ 19, a ≥ 17, c ≥ 14.
Correct Answer is :   a ≤ 20, c ≤ 19, a ≥ 17, c ≥ 14
Q6Paul needs to buy some filing cabinets. He knows that Cabinet A costs $5 per unit, requires 3 square feet of floor space, and holds 4 cubic feet of files. Cabinet B costs $10 per unit, requires 4 square feet of floor space, and holds 6 cubic feet of files. Paul has been given $70 for this purchase, though he don't have to spend that much. The office has room for no more than 36 square feet of cabinets. How many of which model should Paul buy, in order to maximize storage volume?

A. 7 model B cabinets only
B. 12 model A cabinets only
C. 4 model A and 5 model B cabinets
D. 8 model A and 3 model B cabinets

Solutions
Share 
Step: 1
Let x represent the number of model A cabinets and y represent the number of model B cabinets.
Step: 2
Paul's objective is to maximize the storage volume, that is maximize the function V(x, y) = 4x + 6y
  [Cabinet A holds 4 cubic feet of files and Cabinet B holds 6 cubic feet of files.]
Step: 3
Cabinet A costs $5 per unit and cabinet B costs $10 per unit. The amount given for the purchase is $70.
Step: 4
So, 5x + 10y ≤70
  [Inequality for cabinet costs.]
Step: 5
Floor space required for cabinet A is 3 square feet and that of Cabinet B is 4 square feet. The office has room for at most 36 square feet of cabinets.
Step: 6
So, 3x + 4y ≤ 36
  [Inequality for floor space of cabinets.]
Step: 7
x ≥ 0, y ≥ 0
  [Number of cabinets cannot be negative.]
Step: 8
Let's graph the two inequalities on the same coordinate plane to identify the feasible region. By substituting x = 0 and y = 0 individually in the corresponding equations of the inequalities, we get two points(solutions) for each of the equations using which we can draw the graphs.
Step: 9
The solution set of 5x + 10y = 70 consists (0, 7) and (14, 0).
Step: 10
The solution set of 3x + 4y = 36 consists (0, 9) and (12, 0).
Step: 11
The feasible region determined by the above constraints is as shown.
Step: 12

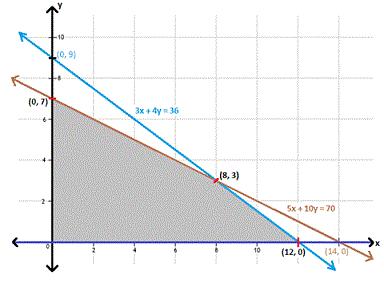
Step: 13
From the figure, the vertices (corner points) of the feasible region are (0, 7), (8, 3) and (12, 0).
Step: 14
Calculate the value of the volume function at each of these vertices to determine which of them has the maximum value. The vertex, at which the value of the volume function is maximized, will be the required solution.
Step: 15
At (0,7), V= 4(0) + 6(7) = 42
  [Substitute x = 0, y =7 in V(x, y).]
Step: 16
At (8, 3), V= 4(8) + 6(3) = 50
  [Substitute x = 8, y = 3 in V(x, y).]
Step: 17
At (12,0), V = 4(12) + 6(0) = 48
  [Substitute x = 12, y = 0 in V(x,y).]
Step: 18
Therefore, the maximum storage volume is 50 cubic feet. This is achieved by buying eight model A and three model B cabinets.
Correct Answer is :   8 model A and 3 model B cabinets
Q7In order to get accurate test results, a lab technician needs to feed the rabbits a daily diet containing a minimum of 12 g of fat, 18 g of carbohydrates, and 8 g of protein. But the rabbits should be fed no more than five ounces of food a day. Rather than order rabbit food that is custom-blended, it is cheaper to order food A and food B, and blend them for an optimal mix. Food A contains 4 g of fat, 6 g of carbohydrates, and 4 g of protein per ounce, and costs $1 per ounce. Food B contains 6 g of fat, 6 g of carbohydrates, and 2 g of protein per ounce, at a cost of $1.50 per ounce. What is the optimal blend ?

A. Two ounces of food A and one ounce of food B
B. One ounce of food A and two ounces of food B
C. Four ounces of food A only
D. Three ounces of food A only

Solutions
Share 
Step: 1
Let x represent the number of ounces of food A and y represent the number of ounces of food B.
Step: 2
The objective of the lab technician is to minimize the total cost for the daily diet of rabbits, that is minimize the function C(x,y) = x + 1.5y
  [Food A costs $1 per ounce and food B costs $ 1.50 per ounce.]
Step: 3
Food A contains 4 g of fat and food B contains 6 g of fat. In daily diet, the minimum quantity of fat required is 12 g.
Step: 4
So, 4x + 6y ≥ 12
  [Inequality for quantity of fat.]
Step: 5
Both food A and food B contain 6 g of carbohydrates each. In daily diet, the minimum quantity of carbohydrates required is 18 g.
Step: 6
So, 6x + 6y ≥ 18
  [Inequality for quantity of carbohydrates.]
Step: 7
Food A contains 4g of protein and food B contains 2 g of protein. In daily diet, the minimum quantity of protein required is 8 g.
Step: 8
So 4x + 2y ≥ 8
  [Inequality for quantity of protein.]
Step: 9
The maximum weight of the food is five ounces.
Step: 10
So, x + y ≤ 5
  [In equality for quantity of food.]
Step: 11
x ≥ 0 , y ≥ 0
  [Quantity of food cannot be negative.]
Step: 12
Let's graph the four inequalities on the same coordinate plane to identify the feasible region. By substituting x = 0 and y = 0 individually in the corresponding equations of the inequalities, we get two points for each of the equations using which we can draw the graphs.
Step: 13
The solution of 4x + 6y = 12 consists (0 , 2) and (3, 0).
Step: 14
The solution set of 6x + 6y = 18 consists (0, 3) and (3, 0).
Step: 15
The solution set of 4x + 2y = 8 consists (0,4) and (2, 0).
Step: 16
The solution set of x + y = 5 consists ( 0, 5) and (5, 0).
Step: 17
The feasible region determined by the above constraints is as shown.
Step: 18

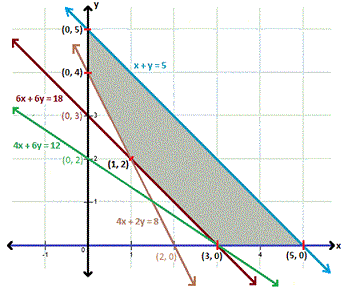
Step: 19
From the figure, the vertices (corner points) of the feasible region are (0,5), (0,4), (1, 2), (3, 0) and (5, 0).
Step: 20
Calculate the value of the cost function at each of these vertices to determine which of them has the minimum value. The vertex, at which the value of the cost function is minimum, will be the required solution.
Step: 21
At (0 ,5) , C = 0 + 1.5(5) = $ 7.50
  [Substitute x = 0, y = 5 in C(x, y).]
Step: 22
At(0,4), C = 0 + 1.5(4) = $6.00
  [Substitute x = 0, y = 4 in C(x, y).]
Step: 23
At (1,2), C = 1 + 1.5(2) = $4.00
  [Substitute x = 1, y = 2 in C (x,y).]
Step: 24
At (3, 0) , C= 3 + 1.5(0) = $3.00
  [Substitute x = 3, y = 0 in C(x, y).]
Step: 25
At (5,0), C = 5 + 1.5(0) = $ 5.00
  [Substitute x = 5, y = 0 in C(x,y).]
Step: 26
Therefore, the minimum cost per daily serving is three dollars. This is achieved using three ounces of food A only.
Correct Answer is :   Three ounces of food A only
Q8Platinum Airlines sells business class and economy class seats for its charter flights. To charter a plane at least 10 business class tickets must be sold and at least 15 economy class tickets must be sold. The plane does not hold more than 40 passengers. Platinum Airlines makes $50 profit for each business class ticket sold and $30 profit for each economy class ticket sold. In order for Platinum Airlines to maximize its profits, how many business class seats should they sell ?
A. 30
B. 20
C. 15
D. 25

Solutions
Share 
Step: 1
Let x represent number of business class tickets sold and y represent number of economy class tickets sold.
Step: 2
The objective of the airlines is to maximize the profit, that is maximize the function P(x, y) = 50 x + 30y
  [Profits on selling each business class and economy class tickets are $50 and $30 respectively.]
Step: 3
x ≥ 10 and y ≥ 15
  [At least 10 business class and 15 economy class tickets must be sold to charter the plane.]
Step: 4
x + y ≤ 40
  [The plane can carry at most 40 passengers.]
Step: 5
Let's graph this inequality on the coordinate plane to identify the feasible region. By substituting x = 0 and y = 0 individually in the corresponding equation of the inequality, we get two points(solutions) for the equation using which we can draw the graph.
Step: 6
The solution set of x + y = 40 consists (0 , 40) and (40, 0).
Step: 7
The feasible region determined by the above constraints is as shown.
Step: 8

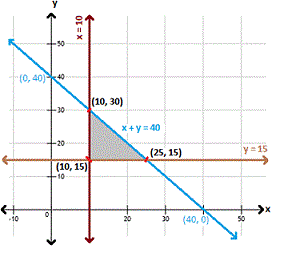
Step: 9
From the figure, the vertices (corner points) of the feasible region are (10, 15), (25, 15) and (10, 30).
Step: 10
Calculate the value of the profit function at each of these vertices to determine which of them has the maximum value. The vertex, at which the value of the profit function is maximum, will be the required solution
Step: 11
At (10, 15), P = 50(10) + 30(15) = $950
  [Substitute x = 10, y = 15 in P(x,y).]
Step: 12
At (25 , 15), P = 50(25) + 30(15) = $1,700
  [Substitute x = 25, y = 15 in P(x,y).]
Step: 13
At (10, 30), P = 50(10) + 30(30) = $1,400
  [Substitute x = 10, y = 30 in P(x,y).]
Step: 14
Therefore, 25 business class seats should be sold to maximize profits.
Correct Answer is :   25
Q9Vitamins C and D are found in two different foods X and Y. One unit of food X contains 4 units of vitamin C and 6 units of vitamin D. One unit of food Y contains 8 units of vitamin C and 4 units of vitamin D. One unit of food X and Y costs $1 and $1.50 respectively. The minimum daily requirement of vitamin C and D for a person are 80 units and 100 units respectively. Assuming that anything is excess of daily minimum requirement of vitamin C and D is not harmful. Find out the optimal mixture of food X and Y at the minimum cost which meets the daily minimum requirement of vitamin C and D.
A. 15 units of food X and 2.5 units of food Y
B. 20 units of food X only
C. 25 units of food Y only
D. 10 units of food X and 8 units of food Y

Solutions
Share 
Step: 1
Let x represent the number of units of food x and y represent the number of units of food y.
Step: 2
Here, the objective is to minimize the total cost, that is minimize the function C(x,y) = x + 1.5 y
  [Food X costs $ 1 per unit and food Y costs $1.50 per unit.]
Step: 3
One unit of food X contains 4 units of vitamin C and that of food Y contains 8 units of vitamin C. In daily diet, the minimum amount of vitamin C required is 80 units.
Step: 4
So, 4x + 8y ≥ 80
  [Inequality for quantity of vitamin C.]
Step: 5
One unit of food X contains 6 units of vitamin D and that of food Y contains 4 units of vitamin D. In daily diet, the minimum amount of vitamin D required is 100 units.
Step: 6
So, 6x + 4y ≥100
  [Inequality for quantity of vitamin D.]
Step: 7
x ≥ 0, y ≥ 0
  [Quantity of food cannot be negative.]
Step: 8
Let's graph the two inequalities on the same coordinate plane to identify the feasible region. By substituting x = 0 and y = 0 individually in the corresponding equations of the inequalities, we get two points(solutions) for each of the equations using which we can draw the graphs.
Step: 9
The solution set of 4x + 8y = 80 consists (0, 10) and (20, 0).
Step: 10
The solution set of 6x + 4y = 100 consists (16.67 , 0) and (0,25).
Step: 11
The feasible region determined by the above constraints is as shown.
Step: 12

Step: 13
From the figure, the vertices(corner points) of the feasible region are (0,25) , (15,2.5), and (20,0).
Step: 14
Calculate the value of the cost function at each of these vertices to determine which of them has the minimum value. The vertex, at which the value of the cost function is minimum, will be the required solution.
Step: 15
At (0,25), C = 0 + 1.5(25) = $37.50
  [Substitute x = 0, y = 25 in C(x,y).]
Step: 16
At (15, 2.5), C = 15 +1.5(2.5) = $18.75
  [Substitute x = 15, y = 2.5 in C(x,y).]
Step: 17
At (20, 0), C = 20 + 1.5(0) = $ 20
  [Substitute x = 20, y = 0 in C(x.y).]
Step: 18
Therefore, the minimum cost that meets the daily minimum requirement of vitamin C and D is $18.75. This is achieved using 15 units of food X and 2.5 units of food Y.
Correct Answer is :   15 units of food X and 2.5 units of food Y
Q10A company manufactures two types of products X and Y and sells them at a profit of $5 on type X and $8 on type Y. Each product is processed on two machines P and Q. Type X requires 3 minutes of processing time on P and 6 minutes on Q, type Y requires 3 minutes on P and 3 minutes on Q. The machine P is available for not more than 6 hours while machine Q is available for 10 hours during one working day. How many products of type X and type Y should be produced each day in order to maximize the profit ?
A. 120 type Y products only
B. 80 type X products and 120 type Y products
C. 60 type X products and 60 type Y products
D. 100 type X products and 40 type Y products

Solutions
Share 
Step: 1
Let x represent the number of products of type X and y represent the number of products of type Y.
Step: 2
The objective of the company is to maximize the profit, that is maximize the function P(x,y) = 5x + 8y
  [Profit on type X product is $5 and profit on type Y product is $8.]
Step: 3
Machine P takes 3 minutes time on type X product and 3 minutes time on type Y product and also given that it is available for at most 6 hours (i.e., 360 minutes) during a working day.
Step: 4
So, 3x + 3y ≤ 360 ⇒ x + y ≤ 120
  [Inequality for working hours on machine P.]
Step: 5
Machine Q takes 6 minutes time on type X product and 3 minutes time on type Y product and also given that it is available for at most 10 hours (i.e., 600 minutes) during a working day.
Step: 6
So, 6x + 3y ≤ 600 ⇒ 2x + y ≤ 200
  [Inequality for working hours on machine Q.]
Step: 7
x ≥ 0, y ≥ 0
  [Number of products cannot be negative.]
Step: 8
Let's graph the two inequalities on the same coordinate plane to identify the feasible region. By substituting x = 0 and y = 0 individually in the corresponding equations of the inequalities, we get two points(solutions) for each of the equations using which we can draw the graphs.
Step: 9
The solution set of x + y = 120 consists (0, 120) and (120, 0).
Step: 10
The solution set of 2x + y = 200 consists (0, 200) and (100, 0).
Step: 11
The feasible region determined by the above constraints is as shown.
Step: 12
From the figure, the vertices (corner points) of the feasible region are (0, 120), (80, 40) and (100, 0).
Step: 13
Calculate the value of the profit function at each of these vertices to determine which of them has the maximum value. The vertex, at which the value of the profit function is maximum, will be the required solution.
Step: 14
At (0, 120), P = 5(0) + 8(120) = $960
  [Substitute x = 0, y = 120 in P(x, y).]
Step: 15
At (80, 40), P = 5(80) + 8(40) = $720
  [Substitute x = 80, y = 40 in P(x, y).]
Step: 16
At (100, 0), P = 5(100) + 8(0) = $500
  [Substitute x = 100, y = 0 in P(x, y).]
Step: 17
Therefore, the maximum profit is $960. This is achieved by manufacturing 120 type Y products only.
Correct Answer is :   120 type Y products only

HighSchool Math