Q1John earns $50 everyday by working for 6 hours. He gets $10 for every extra hour worked. The table shows the relationship between the number of extra hours and John's total earnings per day. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Extra Hours (x)	1	2	3
Total Earnings (y)	60	70	80

A. y = 10x + 50
B. x = 10y + 50
C. y = 10x - 50
D. x = 10y - 50

Q2Holly earns $70 everyday by working for 7 hours. She gets $20 for every extra hour worked. The table shows the relationship between the number of extra hours and Holly's total earnings per day. Use the rate of change to identify a linear equation for the data shown in the table.

Number of Extra Hours (x)	1	2	3
Total Earnings (y)	90	110	130

A. x = 20y + 70
B. y = 20x - 70
C. y = 20x + 70
D. x = 20y - 70

Q3A company spends $100 per month on its workers plus 7% commission on its sales.The table shows the relationship between the sales and expenditure of the company. Use the rate of change to identify a linear equation for the data shown in the table.

Sales Worth (x)	100	200	300	400
Expenditure in Dollars (y)	107	114	121	128

A. x = 0.07y + 100
B. y = 0.07x - 100
C. x = 0.07y - 100
D. y = 0.07x + 100

Q4Which of the following is the appropriate situation in which one quantity changes at a constant rate per unit interval in relation to another?

A. Lucas bought a truck for $22,000 in 1995. The value of the truck increased by 3% in 1996 and by 4% in 1997.
B. Sunny bought a truck for $20,000. The value of the truck decreases by 3% each year. Its value after 2 years should be $18,818.
C. William bought a truck for $20,000 in 1995. The value of the truck increased by 3% in 1996 and then decreased by 3% in 1997. Its value after 2 years should be $18,818.
D. Caleb bought a truck for $21,000 in 1995. The value of the truck decreased by 0.3% in 1996 and by 3% in 1997.

Q5Which of the following is the appropriate situation in which one quantity changes at a constant rate per unit interval in relation to another?

A. The price of gasoline in the year 1995 was $15 per gallon. Its price decreased by 0.3% in the next year and then by 2% in the next two years.
B. The price of gasoline in the year 1995 was $15 per gallon and its price increases by 3% each year. The value of the gasoline after 3 years should be $16.35.
C. The price of gasoline in the year 1995 was $15 per gallon. Its price in 1996 was $15.45 and in 1997 was $15.60.
D. The price of gasoline in the year 1995 was $15 per gallon. Its price decreased by 3% in the next year and then by 2% in the next two years.

Q6Recognize the situation in which one quantity changes at a constant rate per unit interval in relation to another.

A. Revenues of a factory in the subsequent years were 5 billion dollars, 10.3 billion dollars, 21.218 billion dollars, 43.70908 billion dollars and 90.040705 billion dollars.
B. Revenues of a factory in the subsequent years were 2 billion dollars, 3billion dollars, 5 billion dollars, 8 billion dollars and 10 billion dollars.
C. Revenues of an organization in the subsequent years were 5 billion dollars, 9 billion dollars, 11 billion dollars, 15 billion dollars and 90.040705 billion dollars.
D. Revenues of a company in the subsequent years were 5 billion dollars, 10billion dollars, 21.218 billion dollars, 43.70908 billion dollars and 90 billion dollars.

Q7Identify the situation in which one quantity changes at a constant rate per unit interval in relation to another, which has been plotted in the given graph.


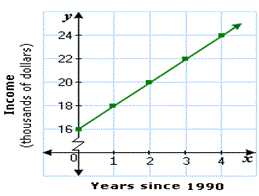
A. Sam′s annual income was $16000 in 1990.Since then, every year his income hasincreased by $2000.
B. Sam′s annual income was $16000 in 1991. Since then, every year his income has increased by $2000.
C. Sam′s annual income was $16000 in 1990. Since then, every year his income has decreased by $2000.
D. Sam′s annual income was $16000 in 1990. Since then, every year his income has increased by $1000.

Q8Recognize the situation in which one quantity changes at a constant rate per unit interval in relation to another.

A. Isabelle deposited $1000 in her account in 2005 and the money grew from $1000 to $5000 in 2 years. Then the $5000 grew to $8000 in the next year.
B. Grace deposited 1000$ in her account in 2005 and the money decreased from $8000 to $ 4000 in 3 years and then from $4000 to $1000 in 1 year.
C. Joe deposited $1000 in his account in 2005 and the money grew from $1000 to $8000 in 3 years, at a constant rate.
D. Angelina deposited $1000 in her account in 2005 and the money grew from $1000 to $6000 in 2 years. Then the $6000 grew to $8000 in the next year.

Q9Identify the situation in which one quantity changes at a constant rate per unit interval relative to another.

A. Caroline invested $750 in a mutual fund in the year 1998. Its value increased by $25 in the subsequent years.
B. Julia invested $750 in a mutual fund in the year 1998. Its value decreased by $25 in the year 1999 and increased by $25 in the year 2000.
C. Gabrielle invested $750 in a mutual fund in the year 1998. Its value increased by $25 in the year 1999 and decreased by $25 in the year 2000.
D. Amelia invested $750 in a mutual fund in the year 1998. Its value decreased by $30 in the year 1999 and by $25 in the year 2000.

Q10Which of the following is the appropriate situation in which one quantity changes at a constant rate per unit interval relative to another?

A. From 1983 through 1989, the number of students in an institute increased by 200. From 1984 through 1987, it increased by 250.
B. From 1983 through 1989, the number of students in an institute increased by 200.
C. From 1983 through 1989, the number of students in an institute decreased by 200. From 1984 through 1987 it increased by 250.
D. From 1983 through 1989, the number of students in an institute increased by 200. From 1984 through 1986 it increased by 300.