Solved Examples and Worksheet for Classifying Relations as Linear or Nonlinear

Q1The table shows the number of miles driven by Tim on each day of his driving practice. Which equation best describes the relationship between the day and the number of miles driven? Is it a linear function?
Day (x)123456
Number of miles (y)71013161922

A. y = 4x + 3; no
B. y = 3x + 4; no
C. y = 3x + 4; yes
D. y = 7x ; yes

Solutions
Share 
Step: 1
As the days go on, the number of miles increases by 3.
  [Observe the table.]
Step: 2
That is, as x increases by a constant number, y also increases by a constant number.
Step: 3
Therefore, the relationship between the day and the number of miles driven can be represented as y = 3x + 4.
Step: 4
So, the situation can be represented by a linear function.
Correct Answer is :   y = 3x + 4; yes
Q2Jeff started a company in 1995. The profits of the company in thousands of dollars are shown in the table. Determine whether this situation can be represented by a linear function or not.
Year (x)199519961997199819992000
Profit (y)15.1826.9568.26139.11239.50369.43

A. No
B. Yes

Solutions
Share 
Step: 1
Observe that there is no constant rate of change in the profit from the table.
Step: 2
That is, as x increases by a constant number, y is not increasing by a constant number.
Step: 3
The graph of these sets of points is not linear.
Step: 4
So, the situation cannot be represented by a linear function.
Correct Answer is :   No
Q3"Flying over the Rainbow", is an online racing game. The software records the date, time and allows the participant to play 12 minutes daily. Determine whether the situation can be represented by a linear function or not.

A. Yes
B. No

Solutions
Share 
Step: 1
The software records the date, time and allows the participant to play 12 minutes daily.
Step: 2
As the days go on, the number of minutes played stays constant.
Step: 3
The graph of these sets of points (number of the day, minutes) form a line.
Step: 4
So, the situation can be represented by a linear function.
Correct Answer is :   Yes
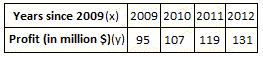
Q4The table shows the profits (in million $) of a company since 2009. Determine whether the situation can be represented by a linear function or not.


A. No
B. Yes

Solutions
Share 
Step: 1
As the years go on, the amount of profit increases by $12 million.
  [Observe the table.]
Step: 2
That is, as x increases by a constant number, y also increases by a constant number.
Step: 3
The graph of these sets of points form a line.
Step: 4
So, the situation can be represented by a linear function.
Correct Answer is :   Yes
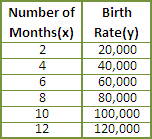
Q5The table shows the birth rate of the children in the United Kingdom in a particular year. Determine whether the situation can be represented by a linear function or not.


A. Yes
B. No

Solutions
Share 
Step: 1
As the number of months increases by 2, the birth rate of the children increases by 20,000.
  [Observe the table.]
Step: 2
That is, as x increases by a constant number, y also increases by a constant number.
Step: 3
The graph of these sets of points form a line.
Step: 4
So, the situation can be represented by a linear function.
Correct Answer is :   Yes
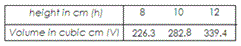
Q6Jacob has cylindrical containers of same radius but different height (h) to measure capacity of the milk. The table below shows the volume of the cylinder of radius 3cm and with different heights (in cm). Is the volume of the cylinder a linear or nonlinear function of the height of the cylinder?

A. Linear Function
B. Non Linear Function
C. None of the above

Solutions
Share 
Step: 1
Observe that there is a constant rate of change in the Volume V from the table.
Step: 2
That is, as the height h increases by a constant number, Volume V is increasing by a constant number.
Step: 3
The graph of these sets of points is linear.
Step: 4
So, the volume of the cylinder is a linear function of the height of the cylinder.
Correct Answer is :   Linear Function
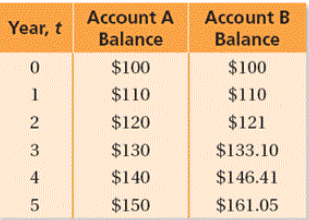
Q7Account A earns simple interest. Account B earns compound interest. The table shows the balances for 5 years. Which of the two situations can be represented by a linear function?


A. Account A
B. Account B
C. Both Account A and Account B
D. Neither Account A nor Account B

Solutions
Share 
Step: 1
Observe that the balance in Account A is increasing at a constant rate of change from the table.
Step: 2
That is, as Year t increases by a constant number, balance in Account A is increasing by a constant number.
Step: 3
The graph of these sets of points is a line.
Step: 4
Observe that the balance in Account B is not increasing at a constant rate of change from the table.
Step: 5
That is, as Year t increases by a constant number, balance in Account B is not increasing by a constant number.
Step: 6
The graph of these sets of points is not linear.
Step: 7
So, the situation of Account A earning on simple interest can be represented by linear function.
Correct Answer is :   Account A
Q8The table below shows the height h (in feet) of a falling parachute jumper at t seconds. Does this situation represent a linear function?

A. No
B. Yes

Solutions
Share 
Step: 1
Observe that the height is decreasing at a constant rate of change from the table.
Step: 2
That is, as t increases by a constant number, height h, is decreasing by a constant number, 15.
Step: 3
The graph of these sets of points is linear.
Step: 4
So, the situation can be represented by a linear function.
Correct Answer is :   Yes
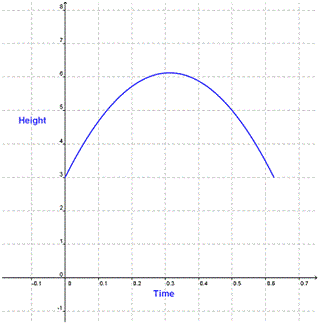
Q9The graph below shows the height off the ground over time for a ball that was tossed in the air and caught. Does this situation represent linear function or non linear function?

A. Linear Function
B. Non Linear Function
C. None of the above

Solutions
Share 
Step: 1
The graph of a linear function is straight line.
Step: 2
The given graph is not a straight line. Therefore, the graph for the given situation represents a non linear function.
Correct Answer is :   Non Linear Function
Q10The graph below shows the temperature (in Celsius) recorded for a week. Is it a linear function or non linear function?

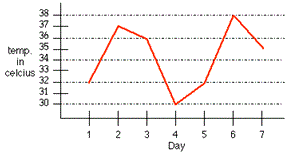
A. Non Linear Function
B. Linear Function
C. None of the above

Solutions
Share 
Step: 1
The graph of a linear function is straight line.
Step: 2
The given graph is not a straight line. Therefore, the graph for the given situation represents a non linear function.
Correct Answer is :   Non Linear Function

HighSchool Math