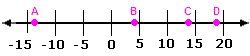
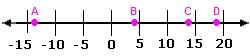
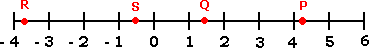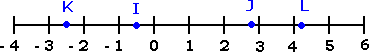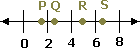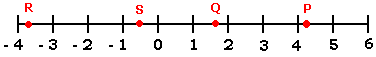Solved Examples and Worksheet for Locating Irrational Numbers on a Number Line

Q1Which of the following is true ?
(I) Any rational number corresponds to a point on the number line, but an irrational number cannot be represented by a point on the number line.
(II) Both rational and irrational numbers can be represented by points on the number line.
(III) Whether it is a rational or irrational number, we cannot represent it as a point on the number line.

A. II and III only
B. I only
C. II only
D. All

Solutions
Share 
Step: 1
From the above statements, "Both rational and irrational numbers can be represented by points on the number line" is the correct statement.
Correct Answer is :   II only
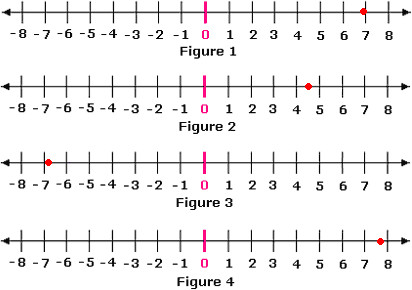
Q2Identify the number line that shows the approximate location of 48.


A. Figure 4
B. Figure 1
C. Figure 2
D. Figure 3

Solutions
Share 
Step: 1
48 = 16×3 = 43
  [16 = 4.]
Step: 2
Approximate value of 3 = 1.732
Step: 3
So, 48 = 4(1.732) = 6.928
Step: 4
Mark the number on the number line.
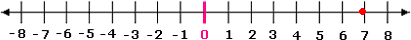
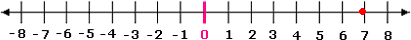
Step: 5
So, Figure 1 represents the approximate location of 48.
Correct Answer is :   Figure 1
Q3Choose the point that represents 18 on the number line.

A. S
B. P
C. Q
D. R

Solutions
Share 
Step: 1
18 = 9 × 2
Step: 2
= 32
  [9 = 3]
Step: 3
Approximate value of 2 = 1.414
Step: 4
18 = 3 × 1.414 = 4.242
Step: 5
The point P approximately represents 4.242.
Step: 6
So, the point P represents 18 on the number line.
Correct Answer is :   P
Q4Choose the point that represents 8 on the number line.

A. J
B. L
C. I
D. K

Solutions
Share 
Step: 1
8 = 4 × 2
Step: 2
= 22
  [4 = 2]
Step: 3
Approximate value of 2 = 1.414
Step: 4
8 = 2 × 1.414 = 2.828
Step: 5
The point J approximately represents 2.828.
Step: 6
So, the point J represents 8 on the number line.
Correct Answer is :   J
Q5Choose the point that represents 3 on the number line.


A. R
B. P
C. S
D. Q

Solutions
Share 
Step: 1
3 lies between the perfect squares 1 and 4.
Step: 2
3 lies between 1 and 4.
Step: 3
1 = 1 and 4 = 2.
Step: 4
3 lies between 0 and 2 on the number line.
Step: 5
So, the point P represents 3 on the number line.
Correct Answer is :   P
Q6Identify the square root that the point represents on the number line.

A. 19
B. 17
C. 10
D. 22

Solutions
Share 
Step: 1
The point on the line lies between 2 and 4.
Step: 2
Among the choices 10 lie between 2 and 4.
Step: 3
So, the point on the number line represents 10.
Correct Answer is :   10
Q7Choose the point that represents 3 on the number line.


A. R
B. S
C. P
D. Q

Solutions
Share 
Step: 1
Approximate value of 3 = 1.732
Step: 2
The point Q approximately represents 1.732
Step: 3
So, the point Q represents 3 on the number line.
Correct Answer is :   Q
Q8Identify the square root that the point represents on the number line.


A. 30
B. 25
C. 2
D. 17

Solutions
Share 
Step: 1
The point on the line lies between 0 and 5.
Step: 2
Among the choices 17, 2 lie between 0 and 5.
Step: 3
The point on the number line is closer to 5.
Step: 4
Among the choices the approximate value of 17 is closer to 5.
Step: 5
So, the point on the number line represents 17.
Correct Answer is :   17
Q9Choose the point that represents - 200 on the number line.


A. B
B. D
C. C
D. A

Solutions
Share 
Step: 1
200 = 14.1421...
Step: 2
- 200 = - 14.1421...
Step: 3
Graph the number.
Step: 4
A is the point that represents - 200 on the number line.
Correct Answer is :   A
Q10Choose the point that represents 200 on the number line.


A. B
B. C
C. A
D. D

Solutions
Share 
Step: 1
200 = 14.1421...
Step: 2
Graph the number.
Step: 3
C is the point that represents 200 on the number line.
Correct Answer is :   C

HighSchool Math