Solved Examples and Worksheet for Approximating Square Roots of Irrational Numbers

Q1Estimate the value of 3619 to the nearest tenth.

A. 6.1
B. 6.3
C. 6.4
D. 6.2

Solutions
Share 
Step: 1
3619
  [Given.]
Step: 2
= 193
  [Find square root of each number.]
Step: 3
= 6.3333...
  [Divide.]
Step: 4
= 6.3
  [Round to the nearest tenth.]
Correct Answer is :   6.3
Q2What is the integer which is nearest to 38?

A. 5
B. 6
C. 8
D. 7

Solutions
Share 
Step: 1
An integer should not have a decimal part. So, the integer nearest to 38 will be the square root of the perfect square nearest to 38.
Step: 2
The perfect square that is nearest to 38 is 36.
Step: 3
So, the integer which is nearest to 38 is 36 = 6.
Correct Answer is :   6
Q3What is the integer nearest to 10?

A. 5
B. 4
C. 3
D. 2

Solutions
Share 
Step: 1
10 is not a perfect square as 10 does not result in an integer value.
Step: 2
The integer nearest to 10 is the square root of the perfect square nearest to 10.
  [An integer must not have a decimal part.]
Step: 3
The perfect square, which is nearest to 10 is 9.
  [9 = 3, which is an integer.]
Step: 4
So, the integer nearest to 10 is 9 = 3
Correct Answer is :   3
Q4What is the approximate value of 22?

A. 8
B. 6
C. 5
D. 9
E. 7

Solutions
Share 
Step: 1
The perfect squares nearest to 22 are 16 and 25.
Step: 2
So, the value of 22 must lie between 4 and 5.
Step: 3
The number 22 is closer to 25 than 16.
Step: 4
So, the approximate value of 22 = 5.
Correct Answer is :   5
Q5What is the approximate value of 22?

A. 10
B. 6
C. 7
D. 5
E. 8

Solutions
Share 
Step: 1
The perfect squares nearest to 22 are 16 and 25.
Step: 2
So, the value of 22 must lie between 4 and 5.
Step: 3
The number 22 is closer to 25 than 16.
Step: 4
So, the approximate value of 22 = 5.
Correct Answer is :   5
Q6Estimate to the nearest integer.
- 79
A. -9
B. -7
C. -8
D. None of the above

Solutions
Share 
Step: 1
79 lies between the perfect squares, 64 and 81.
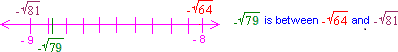
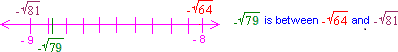
Step: 2
From the above number line, - 79 is nearer to - 81than to - 64.
Step: 3
So, - 79 is closer to - 9 than to - 8.
Step: 4
- 79 ≈ - 9
  [Round to the nearest integer.]
Correct Answer is :   -9
Q7Estimate to the nearest integer.
130 + 23

A. 12
B. 13
C. 11
D. None of the above

Solutions
Share 
Step: 1
130 + 23
  [Original numerical expression.]
Step: 2
130 + 23 = 153
  [Add the terms inside the square root.]
Step: 3
130 + 23 = 153
  [Substitute in the expression.]
Step: 4
153 lies between the perfect squares, 144 and 169 as shown in the following number line.
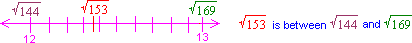
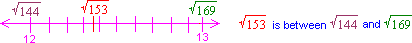
Step: 5
153 is nearer to 144 than to 169.
Step: 6
So, 12 is the nearest integer for the expression.
Correct Answer is :   12
Q8The area of a square is 1345. Approximate the value of this.
A. 45
B. 37
C. 30
D. 40

Solutions
Share 
Step: 1
Find the value of the 1345 using a calculator.
Step: 2
From the calculator, the value of 1345 is 36.674241.
Step: 3
In the decimal number, the digit in tenths place is 6.
Step: 4
As 6 is greater than 5, the decimal 36.6 is closer to 37 .
Step: 5
Therefore, the approximate value of 1345 is 37 .
Correct Answer is :   37
Q9The length of the side of a square is 672. Approximate this length.
A. 30
B. 28
C. 26
D. 25

Solutions
Share 
Step: 1
672 lies between the perfect squares 625 and 676.
Step: 2
672 is nearer to 676, than to 625.
Step: 3
So, the approximate value of 672 is 26.
Correct Answer is :   26
Q10Approximate 174 to the nearest integer.

A. 12
B. 14
C. 16
D. 13

Solutions
Share 
Step: 1
174 lies between the perfect squares 169 and 196.
Step: 2
174 is nearer to 169 than to 196.
Step: 3
Therefore, the approximate integer of 174 is 13.
Correct Answer is :   13
Q11Approximate 32 to the nearest tenth

A. 5
B. 4
C. 6
D. 7

Solutions
Share 
Step: 1
The perfect squares nearest to 32 are 25 and 36.
Step: 2
So, the value of 32 must lie between 5 and 6.
Step: 3
The number 32 is closer to 36 than 25.
Step: 4
So, the approximate value of 32 = 6.
Correct Answer is :   6

HighSchool Math