Solved Examples and Worksheet for Possible Outcomes

Q1Find the number of ways in which Edward can choose a tie, using the tree diagram.


A. 2
B. 6
C. 9
D. 3

Solutions
Share 
Step: 1
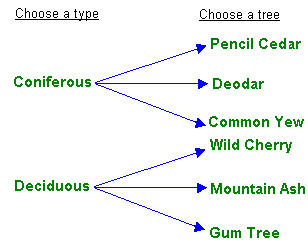
A tree diagram displays all the possible choices where each branch represents a choice.
Step: 2
In the tree diagram, there are 9 different branches representing different choices available.
Step: 3
So, there are 9 different ways in which Edward can choose a tie.
Correct Answer is :   9
Q2Sunny is in an ice-cream parlor. He wants to go to the playground from there. He can go to the playground via his school. There are 2 ways to go to school from the parlor and 3 ways to go to playground from his school. In how many ways can Sunny go to the playground?
A. 8
B. 5
C. 7
D. 6

Solutions
Share 
Step: 1
Total number of possible ways = (Number of ways to go the school from the parlor) × (Number of ways to go to playground from the school)
Step: 2
= 2 × 3
  [Substitute.]
Step: 3
= 6
  [Multiply.]
Step: 4
Sunny can go to the playground from parlor through his school in 6 ways.
Correct Answer is :   6
Q3There are 2 gold coins and 3 silver coins in a box. In how many ways can you choose a pair of a gold coin and a silver coin?
A. 6
B. 8
C. 3
D. 7

Solutions
Share 
Step: 1
Number of ways of choosing a pair = (Number of choices for choosing a gold coin) × (Number of choices for choosing a silver coin)
  [Use the counting principle.]
Step: 2
= 2 × 3 = 6
  [Substitute and multiply.]
Step: 3
So, there are 6 different ways of choosing a pair of a gold coin and a silver coin.
Correct Answer is :   6
Q4In how many ways can a pair of a girl and a boy be formed from a group of 13 boys and 9 girls?
A. 4
B. 117
C. 22
D. 23

Solutions
Share 
Step: 1
Number of ways of making a pair = (Number of boys) × (Number of girls)
  [Use counting principle.]
Step: 2
= 13 × 9 = 117
  [Substitute and simplify.]
Step: 3
Number of pairs that can be formed is 117.
Correct Answer is :   117
Q5Tony has 6 shirts and 5 different trousers. In how many ways can Tony wear these shirts and trousers?

A. 6
B. 5
C. 11
D. 30

Solutions
Share 
Step: 1
Number of ways of choosing a shirt = 6
Step: 2
Number of ways of choosing a trouser = 5
Step: 3
Number of ways that Tony can wear = (Number of ways of choosing a shirt) × (Number of ways of choosing a trouser)
  [Use the counting principle.]
Step: 4
= 6 × 5 = 30
  [Substitute and multiply.]
Step: 5
So, he can wear these shirts and trousers in 30 ways.
Correct Answer is :   30
Q6There are 8 greeting cards and 5 gift items with Holly. Find the number of ways in which Holly can choose a card and a gift item.
A. 45
B. 8
C. 48
D. 40

Solutions
Share 
Step: 1
Number of ways of choosing a pair = (Number of greeting cards available) × (Number of gift items available)
  [Use the counting principle.]
Step: 2
= 8 × 5 = 40
  [Substitute and multiply.]
Step: 3
So, there are 40 different ways of choosing a card and a gift item.
Correct Answer is :   40
Q7List all the possible outcomes when two coins are tossed simultaneously.
A. HT and TH
B. HH and TT
C. HH, HT, TH, and TT
D. None of the above

Solutions
Share 
Step: 1
An outcome is the result of a single trial of an experiment.
Step: 2
The possible outcomes when a single coin is tossed are Head(H) or Tail(T).
Step: 3
The possible outcomes when two coins are tossed simultaneously are HH, HT, TH, and TT.
Correct Answer is :   HH, HT, TH, and TT
Q8Using the tree diagram, find the number of choices of trees available.


A. 4
B. 6
C. 8
D. 10

Solutions
Share 
Step: 1
Each branch of the tree diagram represents the choice of a tree.
Step: 2
So, there are 6 choices of trees available.
Correct Answer is :   6
Q9Joe is throwing a party. He is planning to serve Sandwiches and Ice creams to his guests. He has ordered four different types of Sandwiches: Hamburger (H), Grilled Sandwich (GS), Boiled Sandwich (BS) and Pressed Sandwich (PS), and two different flavors of Ice creams: Chocolate(C) and Strawberry (S). Use a tree diagram and find the number of possible combinations of a Sandwich and Ice cream that Joe can serve to each of his guests.

A. 6
B. 9
C. 8
D. 7

Solutions
Share 
Step: 1
Draw the tree diagram to find the sample space.
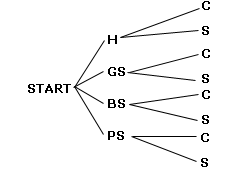
Step: 2
The possible outcomes are (H, C), (H, S), (GS, C), (GS, S), (BS, C), (BS, S), (PS, C) and (PS, S).
Step: 3
So, there are 8 possible combinations of sandwich and ice cream that Joe can serve to each of his guests.
Correct Answer is :   8
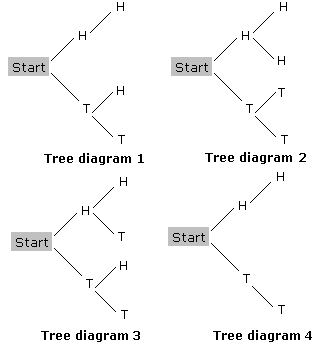
Q10A dime and a penny were tossed at the same time by Richard. Which tree diagram shows all the possible outcomes?

A. Tree diagram 3
B. Tree diagram 1
C. Tree diagram 4
D. Tree diagram 2

Solutions
Share 
Step: 1
The possible outcomes are HH, HT, TH, TT.
Step: 2
So, there are 4 possible outcomes and only the Tree diagram 3 shows them correctly.
Correct Answer is :   Tree diagram 3
Q11Find the number of possible outcomes when the spinner is spun.


A. 6
B. 4
C. 5
D. None of the above

Solutions
Share 
Step: 1
The spinner when spun may land on one of the numbers 0, 1, 3, 4, 5, and 9.
Step: 2
So, the number of possible outcomes is 6.
Correct Answer is :   6
Q12A dime and a penny were tossed at the same time by Richard. Which tree diagram shows all the possible outcomes?

A. Tree diagram 2
B. Tree diagram 4
C. Tree diagram 3
D. Tree diagram 1

Solutions
Share 
Step: 1
The possible outcomes are HH, HT, TH, TT.
Step: 2
So, there are 4 possible outcomes and only the Tree diagram 3 shows them correctly.
Correct Answer is :   Tree diagram 3
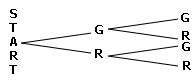
Q13From a bottle containing 1 green ball and 1 red ball, a ball is drawn at random, replaced in the bottle and another ball is drawn. Find the sample space from the tree diagram below.

A. GG, GR, RG, RR
B. GR, RG, RR
C. GG, RR
D. GG, GR, RR

Solutions
Share 
Step: 1
The possible outcomes are GG, GR, RG and RR.
Step: 2
So, the sample space is (GG, GR, RG, RR).
Correct Answer is :   GG, GR, RG, RR
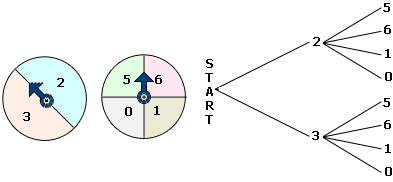
Q14Use the tree diagram to find the number of possible outcomes from spinning the two spinners shown together.

A. 6
B. 2
C. 8
D. 4

Solutions
Share 
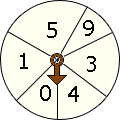
Step: 1
The possible outcomes are (2, 5), (2, 6), (2, 1), (2, 0), (3, 5), (3, 6), (3, 1) and (3, 0).
Step: 2
So, the number of possible outcomes is 8.
Correct Answer is :   8
Q15Use a tree diagram to find the number of ways in which 3 prizes (first, second and third) can be distributed to the 3 students, John, Mike and Joseph, who participated in an essay writing competition.
A. 9
B. 6
C. 12
D. 4

Solutions
Share 
Step: 1
Each student can get 1st, 2nd or 3rd prize.
Step: 2
Make a tree diagram, which represents the prizes given to each of the students as shown below.
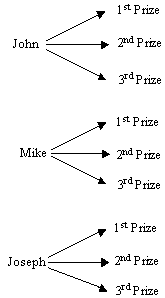
Step: 3
The branches in the tree diagram represent the different ways in which the prizes can be distributed.
Step: 4
So, there are 9 possible ways in which the prizes can be distributed to the students.
Correct Answer is :   9

HighSchool Math